您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“python過擬合實例分析”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
如下圖便直觀形象的展示出這種最嚴重的的過擬合情況:
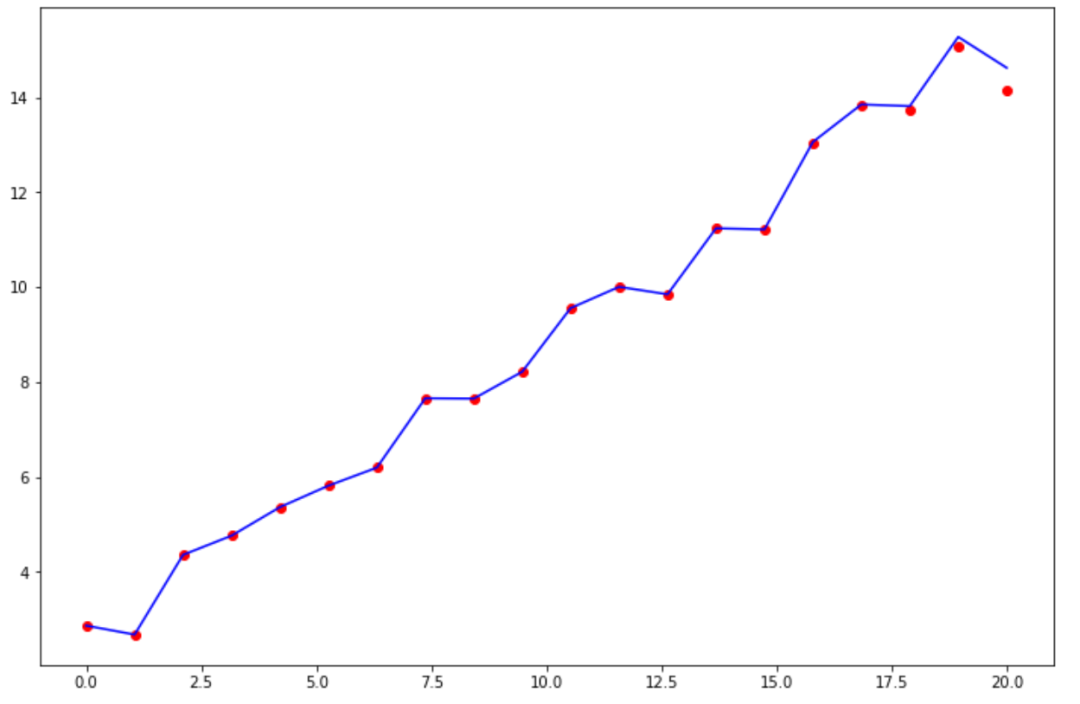
模型幾乎擬合所有點,也就是在訓練集上的準確度接近 100%,這類模型有什么特點呢?不妨看看這個模型的參數:
1.24700471e-13, -2.35752755e-11, 2.06759733e-09, -1.11665116e-07,
4.15722794e-06, -1.13161697e-04, 2.33087852e-03, -3.70886530e-02,
4.61321531e-01, -4.50943817e+00, 3.46373724e+01, -2.07949995e+02,
9.65158102e+02, -3.40164962e+03, 8.85765503e+03, -1.63366853e+04,
1.99303609e+04, -1.41930185e+04, 4.37094529e+03, 2.87198980e+00一共有 20 個,正好等于需要擬合的點數。
以上圖形是用拉格朗日插值方法擬合出來的,借助 scipy 包完成插值,代碼如下所示。
數據準備階段:
from scipy.interpolate import lagrange
import numpy as np
import matplotlib.pyplot as plt
#使用樣本個數
n = 20
# seed 保證每次都生成一個固定隨機數
np.random.seed(2)
eps = np.random.rand(n) * 2
# 構造樣本數據
x = np.linspace(0, 20, n)
y = np.linspace(2, 14, n) + eps調用拉格朗日插值,得到插值函數 p,然后輸入待插值點 x, 完成插值得到插值點(xx,yy)
# 調用拉格朗日插值,得到插值函數p
p = lagrange(x, y)
xx = x
yy = p(xx)拉格朗日插值得到一個多項式模型,參數個數等于樣本個數。
以上我們還原擬合所有樣本點的一個方法。
機器學習中為了模型泛化能力更強,所以需要簡化模型參數,換句話說對參數做正則化處理,這也符合奧卡姆剃刀定律,即簡單有效原理。
常用的L1 正則會使參數稀疏化,它會將其中一些參數權重歸 0. 當然就今天將要擬合的數據點而言,直接簡化模型參數為 2個,擬合效果就不會差。
選用 sklearn 最最簡單的線型回歸模型:
from sklearn import linear_model
reg = linear_model.LinearRegression()
reg.fit(x.reshape(len(x),-1),y)
# 得到2個參數值
reg.coef_,reg.intercept_
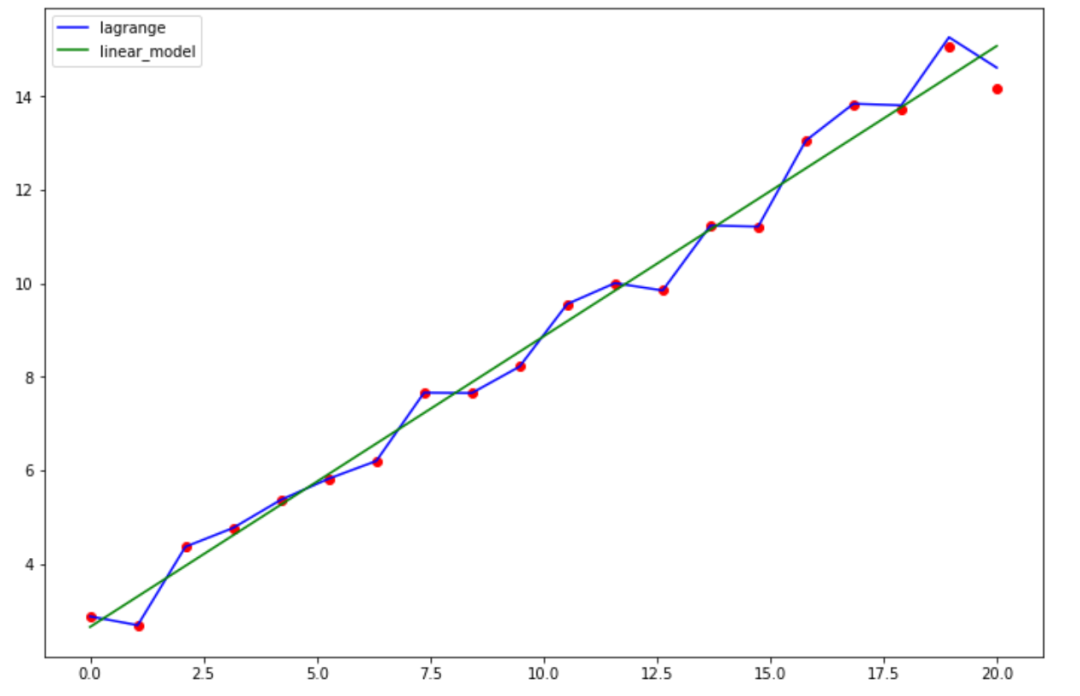
(array([0.62182096]), 2.644854261121125)再plot下擬合效果:
plt.figure(figsize=(12,8))
plt.scatter(x, y, color="r")
# 拉格朗日插值復雜模型
plt.plot(xx, yy, color="b",label='lagrange')
# 線型回歸極簡模型
plt.plot(xx,xx*reg.coef_+reg.intercept_,color='green',label='linear_model')
plt.show()
“python過擬合實例分析”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。