數據分析:OLS回歸分析

　　變量之間存在著相關關系，比如，人的身高和體重之間存在著關系，一般來說，人高一些，體重要重一些，身高和體重之間存在的是不確定性的相關關系。回歸分析是研究相關關系的一種數學工具，它能幫助我們從一個變量的取值區估計另一個變量的取值。

　　OLS(最小二乘法)主要用于線性回歸的參數估計，它的思路很簡單，就是求一些使得實際值和模型估值之差的平方和達到最小的值，將其作為參數估計值。就是說，通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小。最小二乘法可用于曲線擬合，其他一些優化問題也可通過最小化能量或最大化熵用最小二乘法來表達。

　　一，OLS回歸

　　OLS法通過一系列的預測變量來預測響應變量(也可以說是在預測變量上回歸響應變量)。線性回歸是指對參數β為線性的一種回歸(即參數只以一次方的形式出現)模型：

　　Yt=α+βxt+μt (t=1……n)表示觀測數

　　Yt 被稱作因變量

　　xt 被稱作自變量

　　α、β 為需要最小二乘法去確定的參數，或稱回歸系數

　　μt 為隨機誤差項

　　OLS線性回歸的基本原則：最優擬合曲線應該使各點到直線的距離的平方和(即殘差平方和，簡稱RSS)最小：

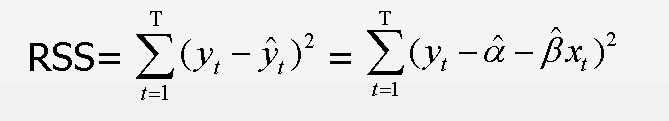
　　OLS線性回歸的目標是通過減少響應變量的真實值與預測值的差值來獲得模型參數(截距項和斜率)，就是使RSS最小。

　　為了能夠恰當地解釋OLS模型的系數，數據必須滿足以下統計假設：

　　正態性：對于固定的自變量值，因變量值成正太分布

　　獨立性：個體之間相互獨立

　　線性相關：因變量和自變量之間為線性相關

　　同方差性：因變量的方差不隨自變量的水平不同而變化，即因變量的方差是不變的

　　二，用lm()擬合回歸模型

　　在R中，擬合回歸模型最基本的函數是lm()，格式為：

　　lm(formula, data)

　　formula中的符號注釋：

　　~ 分割符號，左邊為因變量，右邊為自變量，例如， z~x+y，表示通過x和y來預測z

　　+ 分割預測變量

　　: 表示預測變量的交互項，例如，z~x+y+x:y

　　* 表示所有可能的交互項，例如，z~x*y 展開為 z~x+y+x:y

　　^ 表示交互項的次數，例如，z ~ (x+y)^2，展開為z~x+y+x:y

　　. 表示包含除因變量之外的所有變量，例如，如果只有三個變量x，y和z，那么代碼 z~. 展開為z~x+y+x:y

　　-1 刪除截距項，強制回歸的直線通過原點

　　I() 從算術的角度來解釋括號中的表達式，例如，z~y+I(x^2) 表示的擬合公式是 z=a+by+cx2

　　function 可以在表達式中應用數學函數，例如，log(z) ~x+y

　　對于擬合后的模型(lm函數返回的對象)，可以應用下面的函數，得到模型的更多額外的信息。

　　summary() 展示擬合模型的詳細結果

　　coefficients() 列出捏模型的參數(截距項intercept和斜率)

　　confint() 提供模型參數的置信區間

　　residuals() 列出擬合模型的殘差值

　　fitted() 列出擬合模型的預測值

　　anova() 生成一個擬合模型的方差分析表

　　predict() 用擬合模型對新的數據預測響應變量

學習交流群483787113；進群暗號櫻桃