您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
● 快速排序(Quick Sort)
1、算法描述:
在平均狀況下,排序n個數據要O(nlg(n))次比較。在最壞狀況下則需要O(n^2)次比較,但這種狀況并不常見。事實上,快速排序通常明顯比其他O(nlg(n))算法更快,因為它的內部循環(inner loop)可以在大部分的架構上很有效率地被實現出來,且在大部分真實世界的數據,可以決定設計的選擇,減少所需時間的二次方項的可能性。
2、步驟:
1)從數列中挑出一個元素,稱為 “基準”。
2)重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的后面(相同的數可以到任一邊)。在這個分區退出之后,該基準就處于數列的中間位置。這個稱為分區操作。
3)遞歸把小于基準值元素的子數列和大于基準值元素的子數列排序。
算法優化:
1)如果進行排序的區間較小,快速排序效率較低,可通過插入排序實現
2)對于基準的選取,利用三數取中法,就不會恰好取到最大或最小的數,避免了最快情況的發生
三數取中法(首位、中間和末尾的數據)
int GetMidOfThree(int *arr, int left, int mid, int right)//三數取中法(left,mid和right所在數據中取中間數作為“基準”)
{
assert(arr);
if (arr[left] < arr[mid])
{
if (arr[mid] < arr[right])
{
return arr[mid];
}
else //arr[right]<=arr[mid]
{
if (arr[left] > arr[right])
return arr[left];
else
return arr[right];
}
}
else//arr[left]>=arr[mid]
{
if (arr[mid] > arr[right])
{
return arr[mid];
}
else//arr[right]>=arr[mid]
{
if (arr[right] > arr[left])
return arr[left];
else
return arr[right];
}
}
}對于步驟2,有三種實現方式
int PartSort1(int *arr, int left, int right)//方法一
{//使右邊均為大于key的數,左邊均為小于key的數
assert(arr);
int key = GetMidOfThree(arr, left, left - (left - right) / 2, right);//選取“基準”下標
//int key = arr[left];//也可為right
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && arr[begin] <= key)//從左往右找大于key的數
{
begin++;
}
while (begin < end && arr[end] >= key)//從右往左找小于key的數
{
end--;
}
if (begin < end)//如果begin<end進行交換,相等也可以交換,故該if條件可以不寫
{
swap(arr[begin], arr[end]);
}
}
//此時begin和end相等
if (arr[begin] > arr[right])//處理只有兩個數時eg:2 1;
{
swap(arr[begin], arr[right]);
}
return end;
}
int PartSort2(int *arr, int left, int right)//方法二:挖坑法
{
assert(arr);
//基準為left數據,在進行循環時先進行右邊查找,再進行左邊查找;基準為right時,順序相反
//這樣才能將比key大的數存放在前一部分,比key小的存放在后一部分
//不能用三數取中法選取基準【僅是個人觀點,如有誤請多多指教】
int key = arr[left];
int begin = left;
int end = right;//此處從right處開始
while (begin < end)
{
while (begin < end && arr[end] >= key)//右邊找比key小的數據
{
end--;
}
if (begin < end)
{
arr[begin++] = arr[end];
}
while (begin < end && arr[begin] <= key)//左邊找比key大的數據
{
begin++;
}
if (begin < end)//埋坑。(end--)挖新坑
{
arr[end--] = arr[begin];
}
}
arr[begin] = key;
return end;
}
int PartSort3(int *arr, int left, int right)//方法三:此法更好些(代碼簡單),通過prev和cur遍歷一次進行排序
{
int key = arr[right];//不能用三數取中進行,如果key為arr[left],則循環從后往前進行,找大于key的數進行交換
int prev = left - 1;
int cur = left;
while (cur < right)//從左往右遇大于或等于key的數,跳過去;遇到小于key的數停下來進行交換
{//prev的兩種情況:1、緊跟在cur后面;2、指向比key大的前一個數
if (arr[cur] < key && ++prev != cur)//如果prev和cur緊跟就不進行交換
{
swap(arr[cur], arr[prev]);
}
cur++;
}
swap(arr[++prev], arr[right]);//將prev的后一位與最后元素進行交換
return prev;
}遞歸函數的實現
void QuickSort(int *arr, int left, int right)
{
assert(arr);
if (left >= right)//遞歸退出條件
{
return;
}
if (right - left < 13)//當區間比較小時,用插入排序(提高性能)
{
InsertSort(arr, right - left);
}
//int div = PartSort1(arr, left, right);
//int div = PartSort2(arr, left, right);
int div = PartSort3(arr, left, right);
QuickSort(arr, left, div - 1);
QuickSort(arr, div + 1, right);
}非遞歸實現快速排序
void QuickSort_NonR(int *arr, int left, int right)//快速排序---非遞歸法(利用棧)
{
assert(arr);
stack<int> s;
if (left < right)//兩端數據入棧,right先入棧,left后入棧
{
s.push(right);
s.push(left);
}
while (left < right && !s.empty())
{
//取出要進行數據段的兩端
left = s.top();
s.pop();
right = s.top();
s.pop();
if (left - right < 13)
{
InsertSort(arr, left - right + 1);
}
else
{
int div = PartSort3(arr, left, right);//循環進行,div的右邊后入棧,先進行右邊的排序
if (left < div - 1)
{
s.push(div - 1);
s.push(left);
}
if (right > div + 1)
{
s.push(right);
s.push(div + 1);
}
}
}
}● 歸并排序(Merg Sort)
1、算法描述:
歸并排序是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法的一個非常典型的應用
2、步驟:
1)申請和原序列一樣大的空間,該空間用來存放合并后的序列
2)序列分為兩部分,進行遞歸,先使小的序列有序,在回退使較大序列有序
3)進行兩個序列的合并后,將有序序列回寫到原序列中
具體實現如下:
void _Merg(int *arr, int *tmp, int begin1, int end1, int begin2, int end2)//進行兩個序列的合并
{
assert(arr);
assert(tmp);
int index = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])//小的數據寫入tmp
{
tmp[index] = arr[begin1];
begin1++;
}
else
{
tmp[index] = arr[begin2];
begin2++;
}
index++;
}
//數據多序列的鏈接在tmp后面
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
}
void _MergSort(int *arr, int *tmp, int left, int right)//遞歸使要進行合并的序列有序,再調用合并序列函數
{
assert(arr);
assert(tmp);
if (left >= right)
{
return;
}
int mid = left - (left - right) / 2;
_MergSort(arr, tmp, left, mid);
_MergSort(arr, tmp, mid + 1, right);
//合并后回寫到arr中
_Merg(arr, tmp, left, mid, mid + 1, right);
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
void MergSort(int *arr, int size)
{
assert(arr);
int *tmp = new int[size];//開辟size空間tmp臨時存放部分合并的數據
memset(tmp, 0, size*sizeof(int));//初始化
_MergSort(arr, tmp, 0, size - 1);
delete[] tmp;
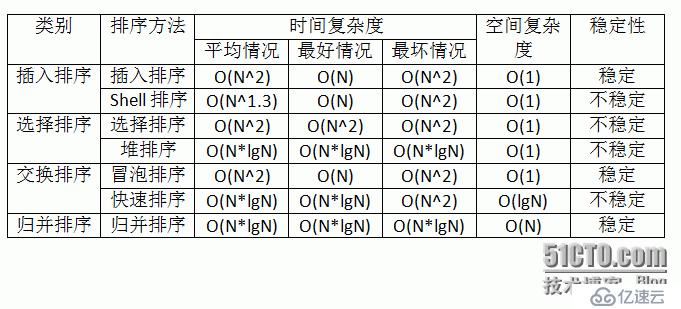
}對于這7種算法的復雜度和穩定性的總結
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。