怎樣從PPI網絡進一步挖掘信息

怎樣從PPI網絡進一步挖掘信息，相信很多沒有經驗的人對此束手無策，為此本文總結了問題出現的原因和解決方法，通過這篇文章希望你能解決這個問題。

從數據庫中得到蛋白質的相互作用信息之后，我們可以構建蛋白質間的相互作用網絡，但是這個網絡是非常復雜的，節點和連線的個數很多，如果從整體上看，很難挖掘出任何有生物學價值的信息，所以我們需要借助一些算法來深入挖掘。

隨著各個數據庫中信息通量的不斷提高，基于網絡的分析方法越來越受歡迎，比如我們常見的蛋白質相互網絡，基因共表達網絡，轉錄因子調控網絡，pathway網絡等等，為了更好的理解后續的數據挖掘算法，首選要對網路的屬性有一些基本了解。

從數據結構上看，我們所說的網絡network是屬于圖Graph這一數據結構的，網絡是一種比較直觀的描述，就是點和點之間的連線，在算法上，為了準確描述一個網絡，通常借助于鄰接矩陣，示意如下

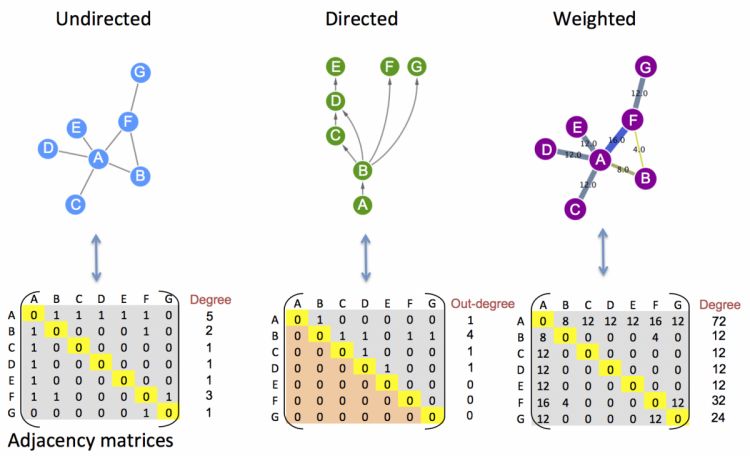
在網絡中，根據節點的連線是否具有方向，可以劃分為有向圖和無向圖兩類，無向圖中被一條線連接的兩個節點其作用是相互的，比如基因共表達網絡，兩個基因間互為共表達基因，而有向圖中，連線是有方向性的，比如轉錄因子調控網絡，轉錄因子調控基因，所以連線由轉錄因子指向某個基因。

無向圖的描述為undirected graph, 有向圖的描述為directed graph。PPI網絡由于蛋白的作用是相互的，所以通常歸類為無向圖。

除了連線的方向性，根據連線對應的值，可以將網絡圖分為加權和非加權兩種， 以基因共表達網絡為例，非加權圖中連線是一個定性描述，兩個基因具有共表達的趨勢，就可以用連線連接，而加權圖是一個定量描述，兩個基因間共表達系數的大小對應邊的值，在可視化時，值不同，對應邊的粗細也不同。

鄰接矩陣可以方便的描述任意一種類別的網絡，如上圖所示，鄰接矩陣是一個二維矩陣，而且是一個方陣，行和列代表的都是圖中的節點，在非加權圖中，0代表兩個節點沒有連線，1代表兩個節點間存在連線；在加權圖中，每個單元格數值對應每條邊的數值。

對于網絡而言，需要了解以下幾個基本概念

1. degree

網絡由節點和邊構成，對于一個節點而言， 該節點連線的多少，即為該節點的degree, 稱之度，對于有向圖，根據連線的防線，度又劃分為入度和出度， 示意如下

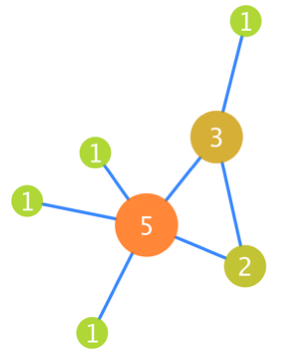
圖中每個節點上標記的數字就是該節點的度數。

2. shorest  path

最短路徑表示兩個節點間的最短距離，在網絡中，從一個節點到另外一個節點，可以有很多個路徑，其中經過的節點數最少的稱之為最短路徑，示意如下

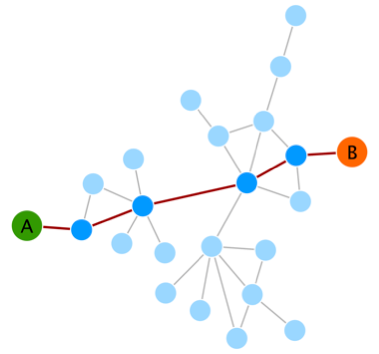
上述到A到B的最短路徑為5。

3. closeness centrality

該統計量用來衡量節點的重要程度，基于最短路徑進行定義，公式如下

4.  Betweenness centrality

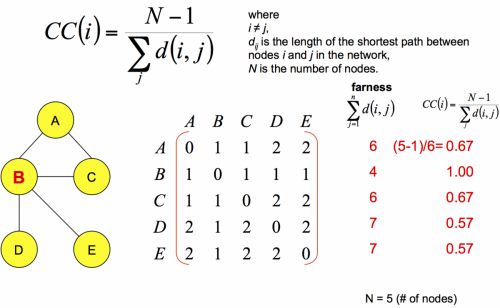
和closeness centrality類似，也是用來表征節點的重要程度，公式如下

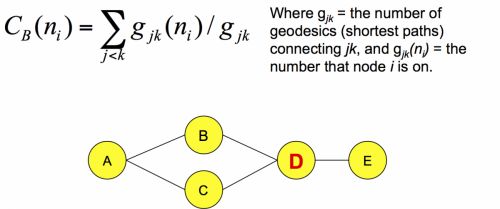
在上圖中。刪除B和C中的任意一個，A都可以連接到E， 但是刪除了D就不行了，所以D就比較重要。

5.  density

密度代表的是網絡中實際的連線數與理論最大連線數的比值，對于包含n個節點的網絡，其最大的變數為任意兩個節點之間都相連，共 n(n-1)/2, 示意如下

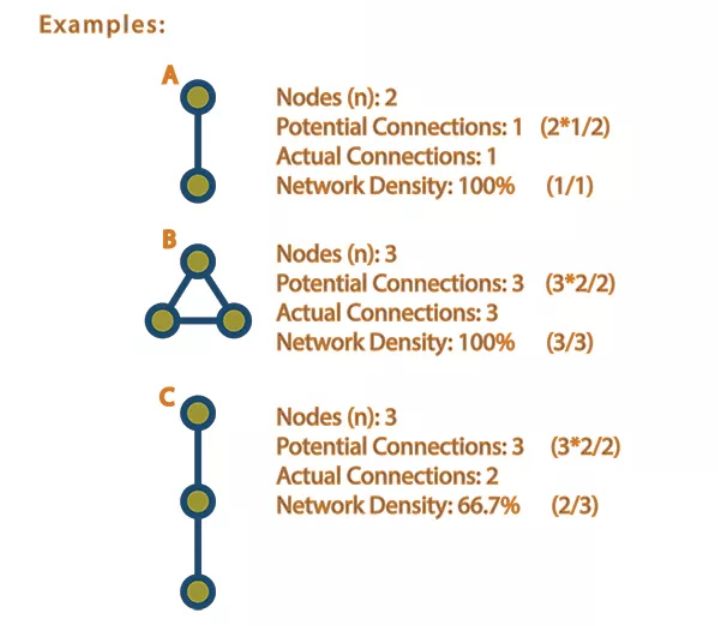
密度用來衡量一個網絡的密集程度。

6.  Clustering Coefficient

聚集系數，和密度類似，也叫做transitity，有兩種定義，第一種稱之為local  clustering coefficient,  針對單個節點進行定義，對于某個節點而言，該統計量的值為與該節點直接相鄰的鄰近節點構成的網絡的密度，示意如下

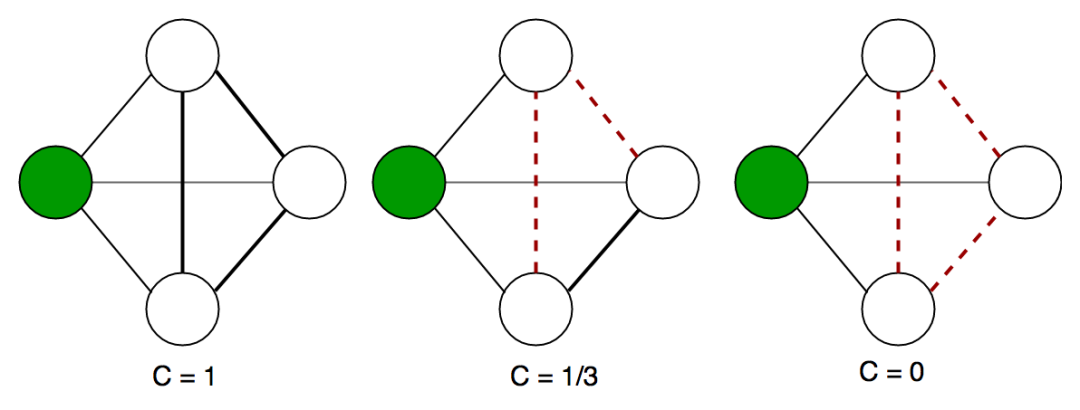
上圖中的第一個網絡，所有節點構成了一個clique, 即完全連通圖，任意兩個節點之間都存在了連線，local clustering coefficient 可以看做是衡量鄰近節點組成的網絡與完全聯通圖接近的程度，取值范圍0到1，越接近于1，越接近一個完全連通圖。

在此基礎上，針對一個網絡，還出現了average  clustering coefficient的概念，就是計算每個節點的local  clustering coefficient， 然后取平均值，公式如下

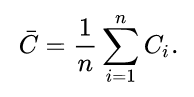
第二種是對于整個網絡而言，稱之為global  clustering coefficient, 這個值的定義是在triangle  graph的基礎上，triangle  graph直譯過來就是三角形圖，即3個節點構成的網絡，示意如下

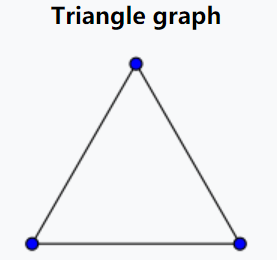
如上圖所示，如果三個節點構成的網絡是一個閉合的三角形，稱之為closed triangle  graph, 如果缺失了其中一條邊，稱之為open  triangle  graph。

global  clustering coefficient 有以下兩種定義方式

有文獻研究發現真實世界的網絡是一個scale-free network, 中文是無標度網絡，意思是說在這個網絡中，大部分的節點其度數都很低，只有部分節點有用很高的度數，示意如下

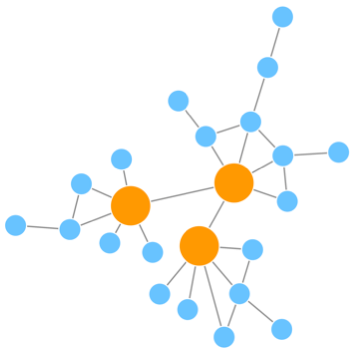
上圖中的網絡就是一個scale-free network, 只有黃色節點的度數較高，藍色節點度數很低，在整個網絡中，大部分都是藍色節點，如果繪制該網絡的節點度數分布圖，應該是如下的一個趨勢

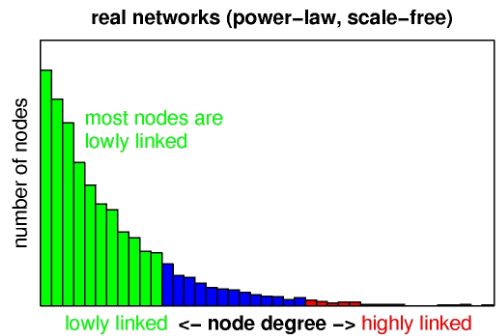
橫坐標為度數，縱坐標為為節點數，度數很低的節點占大多數，度數高的節點只是少數，當然這種描述是一種定性描述，為了準確描述，提出了冪律分布的概念，即上述分布圖對應的表達式為

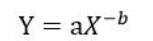
X代表度數，Y代表對應的節點數，有趣的是，將X和Y同時取對數，可以轉換為一個線性方程， 推導如下

取對數之后的分布如下

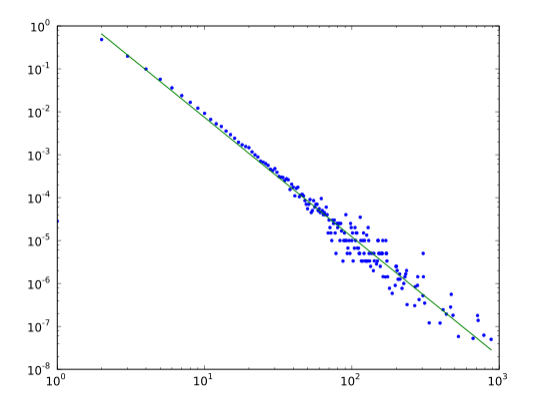
對數轉換之后，可以通過線性擬合確定各個系數的值，在之前的WGCNA中，選擇最佳的power其實就是這個原理，通過比較不同power值條件下，線性擬合的R2值的大小，選擇一個擬合效果最好的值。

在復雜的網絡中，會存在部分密度較高的區域，這樣的區域稱之為community, 也有module等叫法，示意如下

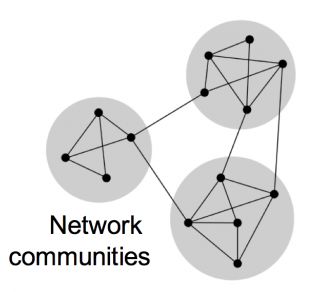
在community內部，連線的密度較高，而區域部分的連線就少。community被認為是具有生物學意義的集合。對于PPI網絡而言，其modules通常有以下兩種生物學含義

1. protein complex
   蛋白質復合體，由多個蛋白質共同組成復合體，然后發揮生物學作用。

2. functional module
   功能模塊，比如位于同一個pathway中的蛋白，其相互作用肯定更加密切。

   
   

所以得到網絡之后，我們需要去識別communities，目前的有多種算法可用選擇，在PPI網絡中，常用的有以下算法

1. MCODE

2. MCL

3. Nwewan-Girvan fast greedy algorithm

   
   

看完上述內容，你們掌握怎樣從PPI網絡進一步挖掘信息的方法了嗎？如果還想學到更多技能或想了解更多相關內容，歡迎關注億速云行業資訊頻道，感謝各位的閱讀！