Dijkstra單源最短路徑算法是什么

本篇內容介紹了“Dijkstra單源最短路徑算法是什么”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

單源最短路徑問題

給定 加權有向圖G=(V,E,W)，每條邊的權值w為 非負數，表示兩個頂點間的距離。
源點s∈V。
求：從s出發到其他各個頂點的最短路徑。
 

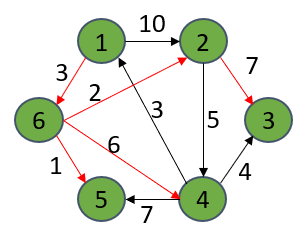
如上圖所示，以1為源點，計算到其余各個頂點的最短距離（我已用紅線標出）。下面列出了最終解：

源點：1
1->6->2 : short[2] = 5
1->6->2->3 : short[3] = 12
1->6->4 : short[4] = 9
1->6->5 : short[5] = 4
1->6v : short[6] = 3

Dijkstra算法相關概念

S集合：當從s到x（x ∈V ）的最短路徑找到時，則x ∈S。當所有頂點都進入S集合時，算法結束。

初始：S=｛s｝，當S=V時算法結束。

從s到u相對于S的最短路徑：指從s到u且僅經過S中頂點的最短路徑。

dist[u]:從s到u相對于S的最短路徑長度

short[u]:從s到u最短路徑的長度（算法最終解）

dist[u] ≥ short[u]

Dijkstra算法采用貪心算法模式，算法過程就是通過計算dist[u],不斷擴充S集合，同時dist[u]會不斷優化改善，直到dist[u] = short[u]，并將其放到S中，當所有頂點都放入S集合時，算法結束。

算法設計思想

輸入：加權有向圖G=(V,E,W)
          V={1,2,…,n}, s=1

輸出：從s到每個頂點的最短路徑

1. 初始S=｛1｝

2. 對于u ∈V-S,計算1到u的相對于S的最短路，長度為dist[u]

3. 選擇V-S中dist值最小的那個頂點，加入S。

4. 繼續上述過程，直到S=V為止。

實例

輸入：G=(V,E,W)，源點1

          V={1,2,3,4,5,6}
 

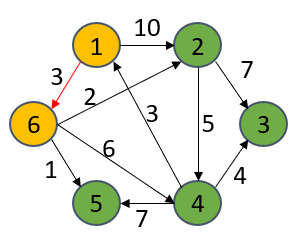
當把6號頂點放進S集合后，經由6號頂點出發到達的頂點的最短距離可能會被優化更新，因為該算法的思想很“貪心”，誰更短我要誰！比如1->6->2要比1->2距離更短，所以dist[2]被更新為5，從專業術語上講，這個“更新”過程叫做松弛，其他點同理。然后從dist[u]里找出最短的路徑的那個頂點（5號），并放進S集合里。

  S={1,6}
  dist[1] = 0
  dist[6] = 3
  dist[2] = 5
  dist[4] = 9
  dist[5] = 4
  dist[3] = ∞

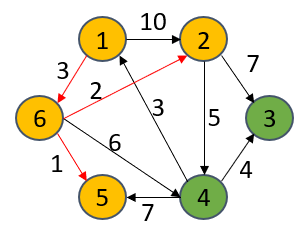
  S={1,6,5,2}
  dist[1] = 0
  dist[6] = 3
  dist[5] = 4
  dist[2] = 5
  dist[4] = 9
  dist[3] = 12

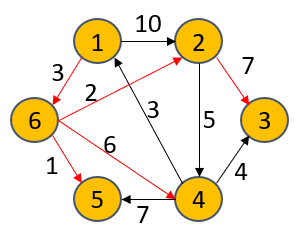
  S={1,6,5,2,4,3}
  dist[1] = 0
  dist[6] = 3
  dist[5] = 4
  dist[2] = 5
  dist[4] = 9
  dist[3] = 12

當有向圖中的所有頂點都進入了S集合后，算法結束，此時的dist[u]的值其實就是最初我們找出的那個最終解short[u]，所以，算法結束時，dist[u]=short[u],得到最終解。

“Dijkstra單源最短路徑算法是什么”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！