您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天就跟大家聊聊有關Dijkstra算法怎么在java中使用,可能很多人都不太了解,為了讓大家更加了解,小編給大家總結了以下內容,希望大家根據這篇文章可以有所收獲。
一、最短路徑的最優子結構性質
該性質描述為:如果P(i,j)={Vi....Vk..Vs...Vj}是從頂點i到j的最短路徑,k和s是這條路徑上的中間頂點,那么P(k,s)必定是從k到s的最短路徑。下面證明該性質的正確性。
假設P(i,j)={Vi....Vk..Vs...Vj}是從頂點i到j的最短路徑,則有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是從k到s的最短距離,那么必定存在另一條從k到s的最短路徑P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。則與P(i,j)是從i到j的最短路徑相矛盾。因此該性質得證。
二、Dijkstra算法
Dijkstra提出按各頂點與源點v間的路徑長度的遞增次序,生成到各頂點的最短路徑的算法。既先求出長度最短的一條最短路徑,再參照它求出長度次短的一條最短路徑,依次類推,直到從源點v 到其它各頂點的最短路徑全部求出為止。
對于下圖:
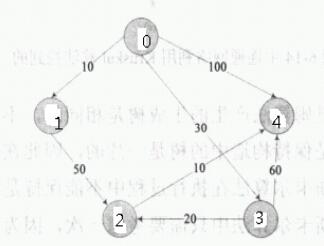
運行結果:
從0出發到0的最短路徑為:0-->0
從0出發到1的最短路徑為:0-->1
從0出發到2的最短路徑為:0-->3-->2
從0出發到3的最短路徑為:0-->3
從0出發到4的最短路徑為:0-->3-->2-->4
=====================================
從0出 發到0的最短距離為:0
從0出 發到1的最短距離為:10
從0出 發到2的最短距離為:50
從0出 發到3的最短距離為:30
從0出 發到4的最短距離為:60
=====================================
public class Dijkstra {
static int M=10000;//(此路不通)
public static void main(String[] args) {
// TODO Auto-generated method stub
int[][] weight1 = {//鄰接矩陣
{0,3,2000,7,M},
{3,0,4,2,M},
{M,4,0,5,4},
{7,2,5,0,6},
{M,M,4,6,0}
};
int[][] weight2 = {
{0,10,M,30,100},
{M,0,50,M,M},
{M,M,0,M,10},
{M,M,20,0,60},
{M,M,M,M,0}
};
int start=0;
int[] shortPath = Dijsktra(weight2,start);
for(int i = 0;i < shortPath.length;i++)
System.out.println("從"+start+"出發到"+i+"的最短距離為:"+shortPath[i]);
}
public static int[] Dijsktra(int[][] weight,int start){
//接受一個有向圖的權重矩陣,和一個起點編號start(從0編號,頂點存在數組中)
//返回一個int[] 數組,表示從start到它的最短路徑長度
int n = weight.length; //頂點個數
int[] shortPath = new int[n]; //存放從start到其他各點的最短路徑
String[] path=new String[n]; //存放從start到其他各點的最短路徑的字符串表示
for(int i=0;i<n;i++)
path[i]=new String(start+"-->"+i);
int[] visited = new int[n]; //標記當前該頂點的最短路徑是否已經求出,1表示已求出
//初始化,第一個頂點求出
shortPath[start] = 0;
visited[start] = 1;
for(int count = 1;count <= n - 1;count++) //要加入n-1個頂點
{
int k = -1; //選出一個距離初始頂點start最近的未標記頂點
int dmin = Integer.MAX_VALUE;
for(int i = 0;i < n;i++)
{
if(visited[i] == 0 && weight[start][i] < dmin)
{
dmin = weight[start][i];
k = i;
}
}
System.out.println("k="+k);
//將新選出的頂點標記為已求出最短路徑,且到start的最短路徑就是dmin
shortPath[k] = dmin;
visited[k] = 1;
//以k為中間點,修正從start到未訪問各點的距離
for(int i = 0;i < n;i++)
{ // System.out.println("k="+k);
if(visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]){
weight[start][i] = weight[start][k] + weight[k][i];
path[i]=path[k]+"-->"+i;
}
}
}
for(int i=0;i<n;i++)
System.out.println("從"+start+"出發到"+i+"的最短路徑為:"+path[i]);
System.out.println("=====================================");
return shortPath;
}
}看完上述內容,你們對Dijkstra算法怎么在java中使用有進一步的了解嗎?如果還想了解更多知識或者相關內容,請關注億速云行業資訊頻道,感謝大家的支持。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。