您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
如何用飛槳復現Capsule Network,相信很多沒有經驗的人對此束手無策,為此本文總結了問題出現的原因和解決方法,通過這篇文章希望你能解決這個問題。
下面讓我們一起來探究Capsule Network網絡結構和原理,并使用飛槳進行復現。
下載安裝命令## CPU版本安裝命令pip install -f https://paddlepaddle.org.cn/pip/oschina/cpu paddlepaddle ## GPU版本安裝命令pip install -f https://paddlepaddle.org.cn/pip/oschina/gpu paddlepaddle-gpu
卷積神經網絡的不足之處
卷積神經網絡(CNN)雖然表現的很優異,但是針對于旋轉或元素平移等變換后的圖片,卻無法做到準確提取特征。
比如,對下圖中字母R進行旋轉、加邊框,CNN會錯誤地認為下圖的三個R是不同的字母。

這就引出了位姿的概念。位姿結合了對象之間的相對關系,在數值上表示為4維位姿矩陣。三維對象之間的關系可以用位姿表示,位姿的本質是對象的平移和旋轉。
對于人類而言,可以輕易辨識出下圖是自由女神像,盡管所有的圖像顯示的角度都不一樣,這是因為人類對圖像的識別并不依賴視角。雖然從沒有見過和下圖一模一樣的圖片,但仍然能立刻知道這些是自由女神像。

此外,人造神經元輸出單個標量表示結果,而膠囊可以輸出向量作為結果。CNN使用卷積層獲取特征矩陣,為了在神經元的活動中實現視角不變性,通過最大池化方法來達成這一點。但是使用最大池化的致命缺點就是丟失了有價值的信息,也沒有處理特征之間的相對空間關系。但是在膠囊網絡中,特征狀態的重要信息將以向量的形式被膠囊封裝。
膠囊的工作原理
讓我們比較下膠囊與人造神經元。下表中Vector表示向量,scalar表示標量,Operation對比了它們工作原理的差異。
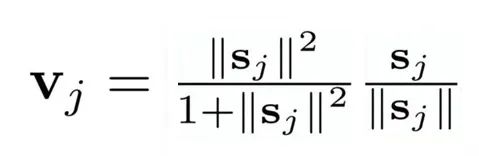
下面將詳剖析這4個步驟的實現原理:
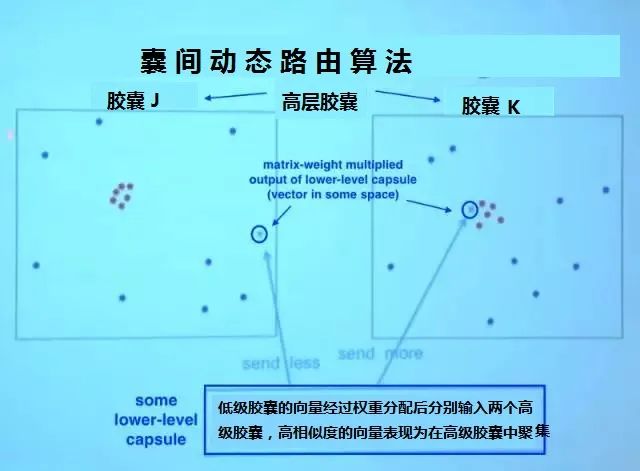
低層膠囊通過加權把向量輸入高層膠囊,同時高層膠囊接收到來自低層膠囊的向量。所有輸入以紅點和藍點表示。這些點聚集的地方,意味著低層膠囊的預測互相接近。
比如,膠囊J和K中都有一組聚集的紅點,因為這些膠囊的預測很接近。在膠囊J中,低層膠囊的輸出乘以相應的矩陣W后,落在了遠離膠囊J中的紅色聚集區的地方;而在膠囊K中,它落在紅色聚集區邊緣,紅色聚集區表示了這個高層膠囊的預測結果。低層膠囊具備測量哪個高層膠囊更能接受其輸出的機制,并據此自動調整權重,使對應膠囊K的權重C變高,對應膠囊J的權重C變低。
關于權重,我們需要關注:
1. 權重均為非負標量。
2. 對每個低層膠囊i而言,所有權重的總和等于1(經過softmax函數加權)。
3. 對每個低層膠囊i而言,權重的數量等于高層膠囊的數量。
4. 這些權重的數值由迭代動態路由算法確定。
對于每個低層膠囊i而言,其權重定義了傳給每個高層膠囊j的輸出的概率分布。
3. 加權輸入向量之和
這一步表示輸入的組合,和通常的人工神經網絡類似,只是它是向量的和而不是標量的和。
4. 向量到向量的非線性變換
CapsNet的另一大創新是新穎的非線性激活函數,這個函數接受一個向量,然后在不改變方向的前提下,壓縮它的長度到1以下。
實現代碼如下:
def squash(self,vector): ''' 壓縮向量的函數,類似激活函數,向量歸一化 Args: vector:一個4維張量 [batch_size,vector_num,vector_units_num,1] Returns: 一個和x形狀相同,長度經過壓縮的向量 輸入向量|v|(向量長度)越大,輸出|v|越接近1 ''' vec_abs = fluid.layers.sqrt(fluid.layers.reduce_sum(fluid.layers.square(vector))) scalar_factor = fluid.layers.square(vec_abs) / (1 + fluid.layers.square(vec_abs)) vec_squashed = scalar_factor * fluid.layers.elementwise_div(vector, vec_abs) return(vec_squashed)
囊間動態路由(精髓所在)
低層膠囊將其輸出發送給對此表示“同意”的高層膠囊。這是動態路由算法的精髓。

▲ 囊間動態路由算法偽代碼
偽代碼的第一行指明了算法的輸入:低層輸入向量經過矩陣乘法得到的?,以及路由迭代次數r。最后一行指明了算法的輸出,高層膠囊的向量Vj。
第2行的bij是一個臨時變量,存放了低層向量對高層膠囊的權重,它的值會在迭代過程中逐個更新,當開始一輪迭代時,它的值經過softmax轉換成cij。在囊間動態路由算法開始時,bij的值被初始化為零(但是經過softmax后會轉換成非零且各個權重相等的cij)。
第3行表明第4-7行的步驟會被重復r次(路由迭代次數)。
第4行計算低層膠囊向量的對應所有高層膠囊的權重。bi的值經過softmax后會轉換成非零權重ci且其元素總和等于1。
如果是第一次迭代,所有系數cij的值會相等。例如,如果我們有8個低層膠囊和10個高層膠囊,那么所有cij的權重都將等于0.1。這樣初始化使不確定性達到最大值:低層膠囊不知道它們的輸出最適合哪個高層膠囊。當然,隨著這一進程的重復,這些均勻分布將發生改變。
第5行,那里將涉及高層膠囊。這一步計算經前一步確定的路由系數加權后的輸入向量的總和,得到輸出向量sj。
第7行進行更新權重,這是路由算法的精髓所在。我們將每個高層膠囊的向量vj與低層原來的輸入向量?逐元素相乘求和獲得內積(也叫點積,點積檢測膠囊的輸入和輸出之間的相似性(下圖為示意圖)),再用點積結果更新原來的權重bi。這就達到了低層膠囊將其輸出發送給具有類似輸出的高層膠囊的效果,刻畫了向量之間的相似性。這一步驟之后,算法跳轉到第3步重新開始這一流程,并重復r次。

▲ 點積運算即為向量的內積(點積)運算,
可以表現向量的相似性。
重復次后,我們計算出了所有高層膠囊的輸出,并確立正確路由權重。下面是根據上述原理實現的膠囊層:
class Capsule_Layer(fluid.dygraph.Layer):
def __init__(self,pre_cap_num,pre_vector_units_num,cap_num,vector_units_num):
'''
膠囊層的實現類,可以直接同普通層一樣使用
Args:
pre_vector_units_num(int):輸入向量維度
vector_units_num(int):輸出向量維度
pre_cap_num(int):輸入膠囊數
cap_num(int):輸出膠囊數
routing_iters(int):路由迭代次數,建議3次
Notes:
膠囊數和向量維度影響著性能,可作為主調參數
'''
super(Capsule_Layer,self).__init__()
self.routing_iters = 3
self.pre_cap_num = pre_cap_num
self.cap_num = cap_num
self.pre_vector_units_num = pre_vector_units_num
for j in range(self.cap_num):
self.add_sublayer('u_hat_w'+str(j),fluid.dygraph.Linear(\
input_dim=pre_vector_units_num,output_dim=vector_units_num))
def squash(self,vector):
'''
壓縮向量的函數,類似激活函數,向量歸一化
Args:
vector:一個4維張量 [batch_size,vector_num,vector_units_num,1]
Returns:
一個和x形狀相同,長度經過壓縮的向量
輸入向量|v|(向量長度)越大,輸出|v|越接近1
'''
vec_abs = fluid.layers.sqrt(fluid.layers.reduce_sum(fluid.layers.square(vector)))
scalar_factor = fluid.layers.square(vec_abs) / (1 + fluid.layers.square(vec_abs))
vec_squashed = scalar_factor * fluid.layers.elementwise_div(vector, vec_abs)
return(vec_squashed)
def capsule(self,x,B_ij,j,pre_cap_num):
'''
這是動態路由算法的精髓。
Args:
x:輸入向量,一個四維張量 shape = (batch_size,pre_cap_num,pre_vector_units_num,1)
B_ij: shape = (1,pre_cap_num,cap_num,1)路由分配權重,這里將會選取(split)其中的第j組權重進行計算
j:表示當前計算第j個膠囊的路由
pre_cap_num:輸入膠囊數
Returns:
v_j:經過多次路由迭代之后輸出的4維張量(單個膠囊)
B_ij:計算完路由之后又拼接(concat)回去的權重
Notes:
B_ij,b_ij,C_ij,c_ij注意區分大小寫哦
'''
x = fluid.layers.reshape(x,(x.shape[0],pre_cap_num,-1))
u_hat = getattr(self,'u_hat_w'+str(j))(x)
u_hat = fluid.layers.reshape(u_hat,(x.shape[0],pre_cap_num,-1,1))
shape_list = B_ij.shape#(1,1152,10,1)
split_size = [j,1,shape_list[2]-j-1]
for i in range(self.routing_iters):
C_ij = fluid.layers.softmax(B_ij,axis=2)
b_il,b_ij,b_ir = fluid.layers.split(B_ij,split_size,dim=2)
c_il,c_ij,b_ir = fluid.layers.split(C_ij,split_size,dim=2)
v_j = fluid.layers.elementwise_mul(u_hat,c_ij)
v_j = fluid.layers.reduce_sum(v_j,dim=1,keep_dim=True)
v_j = self.squash(v_j)
v_j_expand = fluid.layers.expand(v_j,(1,pre_cap_num,1,1))
u_v_produce = fluid.layers.elementwise_mul(u_hat,v_j_expand)
u_v_produce = fluid.layers.reduce_sum(u_v_produce,dim=2,keep_dim=True)
b_ij += fluid.layers.reduce_sum(u_v_produce,dim=0,keep_dim=True)
B_ij = fluid.layers.concat([b_il,b_ij,b_ir],axis=2)
return v_j,B_ij
def forward(self,x):
'''
Args:
x:shape = (batch_size,pre_caps_num,vector_units_num,1) or (batch_size,C,H,W)
如果是輸入是shape=(batch_size,C,H,W)的張量,
則將其向量化shape=(batch_size,pre_caps_num,vector_units_num,1)
滿足:C * H * W = vector_units_num * caps_num
其中 C >= caps_num
Returns:
capsules:一個包含了caps_num個膠囊的list
'''
if x.shape[3]!=1:
x = fluid.layers.reshape(x,(x.shape[0],self.pre_cap_num,-1))
temp_x = fluid.layers.split(x,self.pre_vector_units_num,dim=2)
temp_x = fluid.layers.concat(temp_x,axis=1)
x = fluid.layers.reshape(temp_x,(x.shape[0],self.pre_cap_num,-1,1))
x = self.squash(x)
B_ij = fluid.layers.ones((1,x.shape[1],self.cap_num,1),dtype='float32')/self.cap_num#
capsules = []
for j in range(self.cap_num):
cap_j,B_ij = self.capsule(x,B_ij,j,self.pre_cap_num)
capsules.append(cap_j)
capsules = fluid.layers.concat(capsules,axis=1)
return capsules損失函數
將一個10維one-hot編碼向量作為標簽,該向量由9個零和1個一(正確標簽)組成。在損失函數公式中,與正確的標簽對應的輸出膠囊,系數Tc為1。
如果正確標簽是9,這意味著第9個膠囊輸出的損失函數的Tc為1,其余9個為0。當Tc為1時,公式中損失函數的右項系數為零,也就是說正確輸出項損失函數的值只包含了左項計算;相應的左系數為0,則右項系數為1,錯誤輸出項損失函數的值只包含了右項計算。
|v|為膠囊輸出向量的模長,一定程度上表示了類概率的大小,我們再擬定一個量m,用這個變量來衡量概率是否合適。公式右項包括了一個lambda系數以確保訓練中的數值穩定性(lambda為固定值0.5),這兩項取平方是為了讓損失函數符合L2正則。
def get_loss_v(self,label): ''' 計算邊緣損失 Args: label:shape=(32,10) one-hot形式的標簽 Notes: 這里我調用Relu把小于0的值篩除 m_plus:正確輸出項的概率(|v|)大于這個值則loss為0,越接近則loss越小 m_det:錯誤輸出項的概率(|v|)小于這個值則loss為0,越接近則loss越小 (|v|即膠囊(向量)的模長) ''' #計算左項,雖然m+是單個值,但是可以通過廣播的形式與label(32,10)作差 max_l = fluid.layers.relu(train_params['m_plus'] - self.output_caps_v_lenth) #平方運算后reshape max_l = fluid.layers.reshape(fluid.layers.square(max_l),(train_params['batch_size'],-1))#32,10 #同樣方法計算右項 max_r = fluid.layers.relu(self.output_caps_v_lenth - train_params['m_det']) max_r = fluid.layers.reshape(fluid.layers.square(max_r),(train_params['batch_size'],-1))#32,10 #合并的時候直接用one-hot形式的標簽逐元素乘算便可 margin_loss = fluid.layers.elementwise_mul(label,max_l)\ + fluid.layers.elementwise_mul(1-label,max_r)*train_params['lambda_val'] self.margin_loss = fluid.layers.reduce_mean(margin_loss,dim=1)
編碼器
完整的網絡結構分為編碼器和解碼器,我們先來看看編碼器。
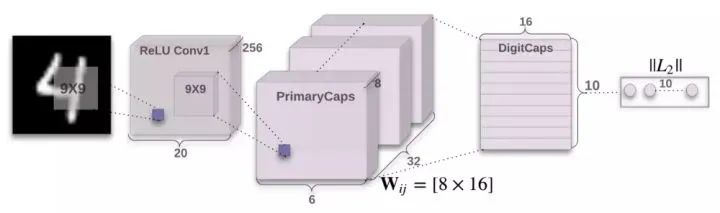
1. 輸入圖片28x28首先經過1x256x9x9的卷積層 獲得256個20x20的特征圖;
2. 用8組256x32x9x9(stride=2)的卷積獲得8組32x6x6的特征圖;
3. 將獲取的特征圖向量化輸入10個膠囊,這10個膠囊輸出向量的長度就是各個類別的概率。
class Capconv_Net(fluid.dygraph.Layer):
def __init__(self):
super(Capconv_Net,self).__init__()
self.add_sublayer('conv0',fluid.dygraph.Conv2D(\
num_channels=1,num_filters=256,filter_size=(9,9),padding=0,stride = 1,act='relu'))
for i in range(8):
self.add_sublayer('conv_vector_'+str(i),fluid.dygraph.Conv2D(\
num_channels=256,num_filters=32,filter_size=(9,9),stride=2,padding=0,act='relu'))
def forward(self,x,v_units_num):
x = getattr(self,'conv0')(x)
capsules = []
for i in range(v_units_num):
temp_x = getattr(self,'conv_vector_'+str(i))(x)
capsules.append(fluid.layers.reshape(temp_x,(train_params['batch_size'],-1,1,1)))
x = fluid.layers.concat(capsules,axis=2) x = self.squash(x)
return x從實現代碼中我們不難看出特征圖轉換成向量實際的過程,是將每組二維矩陣展開成一維矩陣(當然有多個二維矩陣則展開后前后拼接);之后再將所有組的一維矩陣在新的維度拼接形成向量(下圖為示意圖)。根據下面這個思路我經把8次卷積縮小到了一次卷積,本質上脫離循環只用split和concat方法直接向量化,加快了訓練效率。
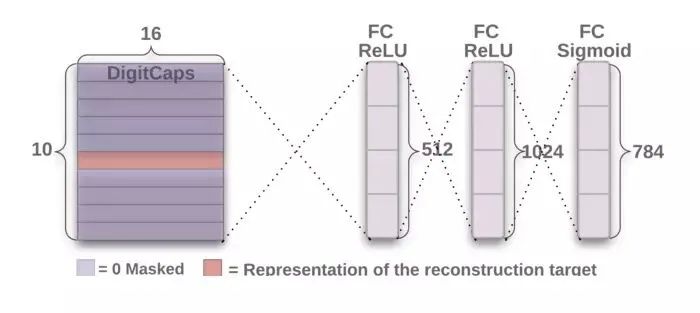
解碼器從正確的膠囊中接受一個16維向量,輸入經過三個全連接層得到784個像素輸出,學習重建一張28×28像素的圖像,損失函數為重建圖像與輸入圖像之間的歐氏距離。
下圖是我自己訓練的網絡重構獲得的圖像,上面是輸入網絡的原圖片,下面是網絡重建的圖片。

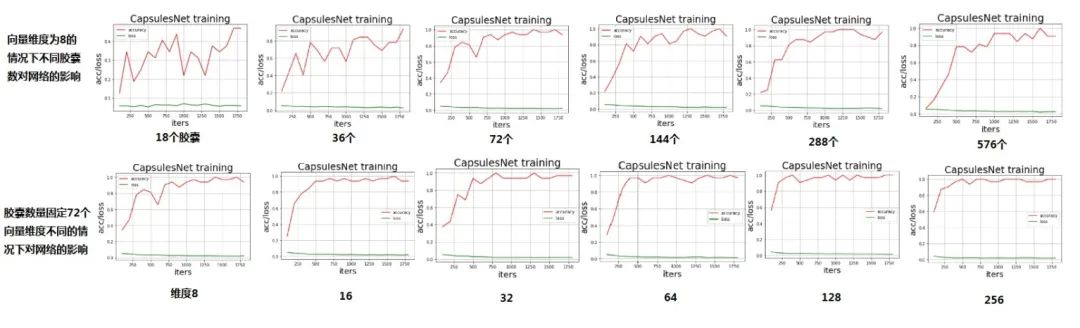
再來玩一下,當訓練到一半時將所有圖片轉置(可以理解為將圖片水平垂直翻轉+旋轉角度,改變位姿)的情況,實驗結論如下。
看完上述內容,你們掌握如何用飛槳復現Capsule Network的方法了嗎?如果還想學到更多技能或想了解更多相關內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。