Java線型代數的核心是什么

本篇內容介紹了“Java線型代數的核心是什么”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

生活中的線性：超市結算

我們想象一個只賣兩個商品的超市，銷售青菜、黃豆。青菜每捆5元，黃豆每盒3元。此外，這個超市還有個積分系統，每捆青菜積分2分，每包黃豆積4分。需要一個結算系統，為客戶計算總價和積分。

這對程序員來說不算挑戰。每個語言都可以輕松的實現，比如用Python:

# By Vameidef bill(x1, x2):
    y1 = 5*x1 + 3*x2
    y2 = 2*x1 + 4*x2
    return 
y1, y2

x1，x2分別為青菜和黃豆的數目。y1，y2為總價和積分。通過輸入不同品種的購買數目，我們得到輸出。這里的輸出有兩個元素：總價和積分。

上面的計算，還可以寫成一組簡單的數學方程：

y1=5×x1+3×x2y1=5×x1+3×x2

y2=2×x1+4×x2y2=2×x1+4×x2

我們試想這樣一種情況：一對夫妻去超市買菜。丈夫買了1捆青菜，2盒黃豆，結賬的時候，為11元和10個積分。妻子買了2捆綁青菜，3盒黃豆，結賬的時候，為19元和16積分。

但如果妻子結賬前碰到丈夫了，倆人把東西放在一起，總共3捆青菜，5盒黃豆。按照我們的結算系統，總價為5×3+3×5=305×3+3×5=30元，總積分為2×3+4×5=262×3+4×5=26積分。

你可能會反駁我，為什么要那么麻煩呢？把剛才的兩個單子加在一起不就可以了。11+19=3011+19=30元，10+16=2610+16=26積分。這通過結算系統的計算結果完全相同。

這想法沒錯。你已經在運用線性系統(Linear System)的思維了：

幾個購物車里的東西，分開結賬的幾張小票的總和，和一次算總帳的結果相同。

線性系統還有更復雜的情況。把兩個購物車給銷售員，讓銷售員按相同的配比，丈夫的來3車，妻子的來2車。那么，新的總價，應該是丈夫的小票乘3，加上妻子的小票乘2。

線性的思維方式是如此的普遍，以致于我們要多想一下，才能想出非線性的例子。下面是一個非線性的情況：超市更改積分系統，積分超過20的話，將獲得雙倍積分。這個時候，如果分開結賬，丈夫和妻子的積分都不到20，那么積分分別為10和16，總和為26。而合在一起結賬，由于積分超過了20，積分將是52。有生活經驗的夫妻們，一定是合在一起結賬，而不是分開結賬了。

我們創造了一個非線性的系統。把這個新的結算系統編成函數，依然用Python：

# By Vameidef non_linear_bill(x1, x2):
    y1 = 5*x1 + 3*x2
    y2 = 2*x1 + 4*x2    if y2 > 20:
        y2 = y2 * 2    return y1, y2

非線性并不是人們的慣常思維方式。超市和商場常有復雜的打折、贈券、積分系統， 這些系統很多時候是非線性的。大腦需要耗費很大能量，才能處理得過來。于是，作為超級線性的男生，我通常的想法都是：去它媽的，老子不要那么麻煩的合單或拆單了。

(奇怪的是，妹紙可以超級熟練的處理各種非線性的購物系統，甚至并行處理多個。上帝拿走的那根肋骨，一定是非線型的……)

“一個”

我們即將要改變我們對一個單位的數據的理解。舉出一個數據

做為程序員，最直接會列舉出一個數據，比如一個整數，一個浮點數。

那一個結構體呢？C語言中的結構體可以包含有多個元素。我們知道，每個元素分開寫出來，并不是結構體的完整數據。比如：

typedef struct {    int veg;    int bean;
} Cart;

再繼續，一個對象的數據呢？一個對象可以有多個屬性。當我們說一個對象的數據時，我們指的是這個對象的多個屬性。比如：

public class Cart{   int veg;   int bean;
}

再比如，我們在說一個人的數據時，包括姓名，身高、體重、IQ多個值。這多個值可以構成這個人的“一個”數據。我們可以在SQL數據庫中建立這樣一個Person(name, height, weight, IQ)的表。每一行，也就是一個記錄(record)，算是一個數據單位。

即使是列表這樣的數據容器，如果固定每個位置數據的意義，那么一個列表也可以算是“一個”數據。比如丈夫購物車為[1，2]，妻子的購物車為[2，3]。

這種包含了多個元素的數據，稱為向量(vector)。與之對應，一個單一的數值，稱為標量(scalar)。

 一個向量

我們用帶小箭頭字母表示，來表示一個向量。比如丈夫的購物車：

x? =[12]x→=[12]

向量可以相加減，這時只需要對應行的元素相加就可以，相當于合并或分開購物車。比如丈夫和妻子的購物車合并：

[12]+[23]=[35][12]+[23]=[35]

向量也可以與一個標量相乘。比如x? ×5x→×5表示5個購物車的量。這時只需將標量與向量的各行元素相乘。

5[12]=[510]5[12]=[510]

伴隨著向量，有一個簡單的概念，即維度(dimension)。上面的購物車向量，包含了兩個數值，即青菜的數目和黃豆的數目。我們因此說該向量是二維的。而結構體中元素的個數、對象的屬性個數，都是維度。我會在以后的文章中深入維度這一概念。

有了對數據的深入理解，那么線性系統的特點可以總結如下： 

L(aD1→+bD2→)=aL(D1→)+bL(D2→)L(aD1→+bD2→)=aL(D1→)+bL(D2→)

D1→D1→和D2→D2→是向量，分別是丈夫和妻子的購物車。而a, b為兩個標量，比如a為2，b為3，表示丈夫那樣的購物車乘2，妻子的購物車乘3。L為結算系統。方程右邊表示，合在一起結賬。方程右邊表示，丈夫和妻子分開小票，相乘再相加。方程的兩邊相等。

矩陣革命

在數學上，我們已經有一組方程表示出了一個線性系統。上面的方程組有些不方便的地方：

• 輸入的元素(黃豆數目)和系統參數(單價)混合在一起

• 有很多字母

數學家是偷懶的動物，這點和程序員很像。他們最后找到了一種省事的記述方式。利用剛才的向量。分離的表示輸入、線性系統和輸出的關系：

[1110]=[5234][12][1110]=[5324][12]

方程最左是個向量，最右是個向量。奇怪的是中間用括號括住的一堆數字。這被稱為一個矩陣(Matrix)。可以看到，這個矩陣中有四個元素，包含了各個物品的單價和各個物品可獲得的積分。這通常是結算系統所包含的數據。我們可以猜測到，這個矩陣相當于一個結算系統。左邊的向量是輸出，右邊的向量是輸入。

結算系統

這個結算系統運作時，把輸入向量放橫，再和結算系統的每一行元素分別相乘，即獲得對應的輸出元素。比如輸出的第一個元素：

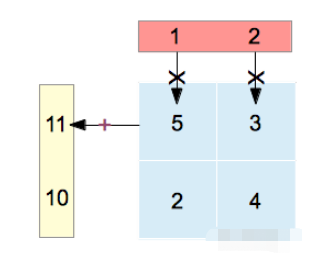
根據這一運算規則，一個線性系統就完全用一個矩陣表示出來了。

可以把矩陣表示成字母A，那么用代數的形式，寫出輸出和矩陣、輸入的關系：

y? =Ax? y→=Ax→

這個代數形式，在線性代數中，有基礎性的地位。方程的右邊，我們說矩陣和向量進行了“乘法”運算。這一運算的規則，是按照我們上面所描述的那樣運行的。這簡直是對乘法符號的一次“運算符重載”(operator overload)。

我們可以用程序來實現上面的計算過程。編寫類似的C程序并不復雜。更方便的是調用現有的庫函數，比如Python中的numpy: 

# By Vameiimport numpy as np# matrixa = np.matrix([[5, 3],[2, 4]])# input Vectorx = np.array([[1], [2]])# multiplicationy = np.dot(a, x)print(y)

矩陣這個東西把結算系統的表示方式大大縮減。更重要在于，線性系統和矩陣是互通的。矩陣表示的是一個線性系統。一個線性系統也總可以表示一個矩陣(證明從略)。

繞了半天，矩陣 = 線性系統。

“Java線型代數的核心是什么”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！