Java如何實現笛卡爾積算法

小編給大家分享一下Java如何實現笛卡爾積算法，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

具體如下：

笛卡爾積算法的Java實現：

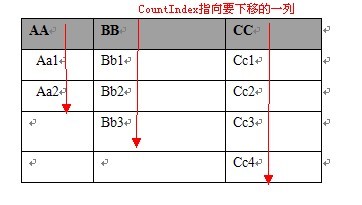
（1）循環內，每次只有一列向下移一個單元格，就是CounterIndex指向的那列。
（2）如果該列到尾部了，則這列index重置為0，而CounterIndex則指向前一列，相當于進位，把前列的index加一。
（3）最后，由生成的行數來控制退出循環。

public class Test {
 private static String[] aa = { "aa1", "aa2" };
 private static String[] bb = { "bb1", "bb2", "bb3" };
 private static String[] cc = { "cc1", "cc2", "cc3", "cc4" };
 private static String[][] xyz = { aa, bb, cc };
 private static int counterIndex = xyz.length - 1;
 private static int[] counter = { 0, 0, 0 };
 public static void main(String[] args) throws Exception {
  for (int i = 0; i < aa.length * bb.length * cc.length; i++) {
   System.out.print(aa[counter[0]]);
   System.out.print("\t");
   System.out.print(bb[counter[1]]);
   System.out.print("\t");
   System.out.print(cc[counter[2]]);
   System.out.println();
   handle();
  }
 }
 public static void handle() {
  counter[counterIndex]++;
  if (counter[counterIndex] >= xyz[counterIndex].length) {
   counter[counterIndex] = 0;
   counterIndex--;
   if (counterIndex >= 0) {
    handle();
   }
   counterIndex = xyz.length - 1;
  }
 }
}

輸出共2*3*4=24行：

aa1 bb1 cc1
aa1 bb1 cc2
aa1 bb1 cc3
aa1 bb1 cc4
aa1 bb2 cc1
aa1 bb2 cc2
aa1 bb2 cc3
aa1 bb2 cc4
aa1 bb3 cc1
aa1 bb3 cc2
aa1 bb3 cc3
aa1 bb3 cc4
aa2 bb1 cc1
aa2 bb1 cc2
aa2 bb1 cc3
aa2 bb1 cc4
aa2 bb2 cc1
aa2 bb2 cc2
aa2 bb2 cc3
aa2 bb2 cc4
aa2 bb3 cc1
aa2 bb3 cc2
aa2 bb3 cc3
aa2 bb3 cc4

最近碰到了一個笛卡爾積的算法要求，比如傳遞過來的參數是"1,3,6,7==4,5,8,9==3,4==43,45,8,9==35,4"，則返回的是一個list，如[1,4,3,43,35][1,4,3,43,4][1,4,3,45,35]……，該list包含是4*4*2*4*2=256個元素，現在的思路是這樣的：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class DescartesTest {
 /**
  * 獲取N個集合的笛卡爾積
  *
  * 說明：假如傳入的字符串為："1,2,3==5,6==7,8"
  *  轉換成字符串數組為：[[1, 2, 3], [5, 6], [7, 8]]
  *  a=[1, 2, 3]
  *  b=[5, 6]
  *  c=[7, 8]
  *  其大小分別為：a_length=3，b_length=2，c_length=2，
  *  目標list的總大小為：totalSize=3*2*2 = 12
  *  對每個子集a，b，c，進行循環次數=總記錄數/(元素個數*后續集合的笛卡爾積個數)
  *  對a中的每個元素循環次數=總記錄數/(元素個數*后續集合的笛卡爾積個數)=12/(3*4)=1次，每個元素每次循環打印次數：后續集合的笛卡爾積個數=2*2個
  *  對b中的每個元素循環次數=總記錄數/(元素個數*后續集合的笛卡爾積個數)=12/(2*2)=3次，每個元素每次循環打印次數：后續集合的笛卡爾積個數=2個
  *  對c中的每個元素循環次數=總記錄數/(元素個數*后續集合的笛卡爾積個數)=12/(2*1)=6次，每個元素每次循環打印次數：后續集合的笛卡爾積個數=1個
  *
  *  運行結果：
  *  [[1, 2, 3], [5, 6], [7, 8]]
   1,5,7,
   1,5,8,
   1,6,7,
   1,6,8,
   2,5,7,
   2,5,8,
   2,6,7,
   2,6,8,
   3,5,7,
   3,5,8,
   3,6,7,
   3,6,8]
   從結果中可以看到：
   a中的每個元素每個元素循環1次，每次打印4個
   b中的每個元素每個元素循環3次，每次打印2個
   c中的每個元素每個元素循環6次，每次打印1個
  *
  * @param args
  */
 public static void main(String[] args) {
  // TODO Auto-generated method stub
  String str ="1,3,6,7==4,5,8,9==3,4==43,45,8,9==35,4";
  List<String> result = descartes(str);
  System.out.println(result);
 }
 @SuppressWarnings("rawtypes")
 public static List<String> descartes(String str) {
  String[] list = str.split("==");
  List<List> strs = new ArrayList<List>();
  for(int i=0;i<list.length;i++){
  strs.add(Arrays.asList(list[i].split(",")));
  }
  System.out.println(strs);
  int total = 1;
  for(int i=0;i<strs.size();i++){
   total*=strs.get(i).size();
  }
  String[] mysesult = new String[total];
  int now = 1;
  //每個元素每次循環打印個數
  int itemLoopNum = 1;
  //每個元素循環的總次數
  int loopPerItem =1;
  for(int i=0;i<strs.size();i++){
   List temp = strs.get(i);
   now = now*temp.size();
   //目標數組的索引值
   int index=0;
   int currentSize = temp.size();
   itemLoopNum = total/now;
   loopPerItem = total/(itemLoopNum*currentSize);
   int myindex = 0;
   for(int j=0;j<temp.size();j++){
    //每個元素循環的總次數
    for(int k=0;k<loopPerItem;k++){
     if(myindex==temp.size())
      myindex=0;
     //每個元素每次循環打印個數
     for(int m=0;m<itemLoopNum;m++){
      mysesult[index]=(mysesult[index]==null?"":mysesult[index]+",")+((String)temp.get(myindex));
      index++;
     }
     myindex++;
    }
   }
  }
  return Arrays.asList(mysesult);
 }
}

運行結果輸出：

[[1, 3, 6, 7], [4, 5, 8, 9], [3, 4], [43, 45, 8, 9], [35, 4]]
[1,4,3,43,35, 1,4,3,43,4, 1,4,3,45,35, 1,4,3,45,4, 1,4,3,8,35, 1,4,3,8,4, 1,4,3,9,35, 1,4,3,9,4, 1,4,4,43,35, 1,4,4,43,4, 1,4,4,45,35, 1,4,4,45,4, 1,4,4,8,35, 1,4,4,8,4, 1,4,4,9,35, 1,4,4,9,4, 1,5,3,43,35, 1,5,3,43,4, 1,5,3,45,35, 1,5,3,45,4, 1,5,3,8,35, 1,5,3,8,4, 1,5,3,9,35, 1,5,3,9,4, 1,5,4,43,35, 1,5,4,43,4, 1,5,4,45,35, 1,5,4,45,4, 1,5,4,8,35, 1,5,4,8,4, 1,5,4,9,35, 1,5,4,9,4, 1,8,3,43,35, 1,8,3,43,4, 1,8,3,45,35, 1,8,3,45,4, 1,8,3,8,35, 1,8,3,8,4, 1,8,3,9,35, 1,8,3,9,4, 1,8,4,43,35, 1,8,4,43,4, 1,8,4,45,35, 1,8,4,45,4, 1,8,4,8,35, 1,8,4,8,4, 1,8,4,9,35, 1,8,4,9,4, 1,9,3,43,35, 1,9,3,43,4, 1,9,3,45,35, 1,9,3,45,4, 1,9,3,8,35, 1,9,3,8,4, 1,9,3,9,35, 1,9,3,9,4, 1,9,4,43,35, 1,9,4,43,4, 1,9,4,45,35, 1,9,4,45,4, 1,9,4,8,35, 1,9,4,8,4, 1,9,4,9,35, 1,9,4,9,4, 3,4,3,43,35, 3,4,3,43,4, 3,4,3,45,35, 3,4,3,45,4, 3,4,3,8,35, 3,4,3,8,4, 3,4,3,9,35, 3,4,3,9,4, 3,4,4,43,35, 3,4,4,43,4, 3,4,4,45,35, 3,4,4,45,4, 3,4,4,8,35, 3,4,4,8,4, 3,4,4,9,35, 3,4,4,9,4, 3,5,3,43,35, 3,5,3,43,4, 3,5,3,45,35, 3,5,3,45,4, 3,5,3,8,35, 3,5,3,8,4, 3,5,3,9,35, 3,5,3,9,4, 3,5,4,43,35, 3,5,4,43,4, 3,5,4,45,35, 3,5,4,45,4, 3,5,4,8,35, 3,5,4,8,4, 3,5,4,9,35, 3,5,4,9,4, 3,8,3,43,35, 3,8,3,43,4, 3,8,3,45,35, 3,8,3,45,4, 3,8,3,8,35, 3,8,3,8,4, 3,8,3,9,35, 3,8,3,9,4, 3,8,4,43,35, 3,8,4,43,4, 3,8,4,45,35, 3,8,4,45,4, 3,8,4,8,35, 3,8,4,8,4, 3,8,4,9,35, 3,8,4,9,4, 3,9,3,43,35, 3,9,3,43,4, 3,9,3,45,35, 3,9,3,45,4, 3,9,3,8,35, 3,9,3,8,4, 3,9,3,9,35, 3,9,3,9,4, 3,9,4,43,35, 3,9,4,43,4, 3,9,4,45,35, 3,9,4,45,4, 3,9,4,8,35, 3,9,4,8,4, 3,9,4,9,35, 3,9,4,9,4, 6,4,3,43,35, 6,4,3,43,4, 6,4,3,45,35, 6,4,3,45,4, 6,4,3,8,35, 6,4,3,8,4, 6,4,3,9,35, 6,4,3,9,4, 6,4,4,43,35, 6,4,4,43,4, 6,4,4,45,35, 6,4,4,45,4, 6,4,4,8,35, 6,4,4,8,4, 6,4,4,9,35, 6,4,4,9,4, 6,5,3,43,35, 6,5,3,43,4, 6,5,3,45,35, 6,5,3,45,4, 6,5,3,8,35, 6,5,3,8,4, 6,5,3,9,35, 6,5,3,9,4, 6,5,4,43,35, 6,5,4,43,4, 6,5,4,45,35, 6,5,4,45,4, 6,5,4,8,35, 6,5,4,8,4, 6,5,4,9,35, 6,5,4,9,4, 6,8,3,43,35, 6,8,3,43,4, 6,8,3,45,35, 6,8,3,45,4, 6,8,3,8,35, 6,8,3,8,4, 6,8,3,9,35, 6,8,3,9,4, 6,8,4,43,35, 6,8,4,43,4, 6,8,4,45,35, 6,8,4,45,4, 6,8,4,8,35, 6,8,4,8,4, 6,8,4,9,35, 6,8,4,9,4, 6,9,3,43,35, 6,9,3,43,4, 6,9,3,45,35, 6,9,3,45,4, 6,9,3,8,35, 6,9,3,8,4, 6,9,3,9,35, 6,9,3,9,4, 6,9,4,43,35, 6,9,4,43,4, 6,9,4,45,35, 6,9,4,45,4, 6,9,4,8,35, 6,9,4,8,4, 6,9,4,9,35, 6,9,4,9,4, 7,4,3,43,35, 7,4,3,43,4, 7,4,3,45,35, 7,4,3,45,4, 7,4,3,8,35, 7,4,3,8,4, 7,4,3,9,35, 7,4,3,9,4, 7,4,4,43,35, 7,4,4,43,4, 7,4,4,45,35, 7,4,4,45,4, 7,4,4,8,35, 7,4,4,8,4, 7,4,4,9,35, 7,4,4,9,4, 7,5,3,43,35, 7,5,3,43,4, 7,5,3,45,35, 7,5,3,45,4, 7,5,3,8,35, 7,5,3,8,4, 7,5,3,9,35, 7,5,3,9,4, 7,5,4,43,35, 7,5,4,43,4, 7,5,4,45,35, 7,5,4,45,4, 7,5,4,8,35, 7,5,4,8,4, 7,5,4,9,35, 7,5,4,9,4, 7,8,3,43,35, 7,8,3,43,4, 7,8,3,45,35, 7,8,3,45,4, 7,8,3,8,35, 7,8,3,8,4, 7,8,3,9,35, 7,8,3,9,4, 7,8,4,43,35, 7,8,4,43,4, 7,8,4,45,35, 7,8,4,45,4, 7,8,4,8,35, 7,8,4,8,4, 7,8,4,9,35, 7,8,4,9,4, 7,9,3,43,35, 7,9,3,43,4, 7,9,3,45,35, 7,9,3,45,4, 7,9,3,8,35, 7,9,3,8,4, 7,9,3,9,35, 7,9,3,9,4, 7,9,4,43,35, 7,9,4,43,4, 7,9,4,45,35, 7,9,4,45,4, 7,9,4,8,35, 7,9,4,8,4, 7,9,4,9,35, 7,9,4,9,4]

遞歸算法：

public static void fn(List<String[]> list,String[] arr,String str){
//迭代list
 List<String> li = new ArrayList<String>();
  for(int i=0;i<list.size();i++){
   //取得當前的數組
   if(i==list.indexOf(arr)){
    //迭代數組
    System.out.println(arr.length);
    for(String st : arr){
     st = str + st;
     if(i<list.size()-1){
      fn(list,list.get(i+1),st);
     }else if(i==list.size()-1){
      li.add(st);
     }
    }
   }
  }
  for(int i = 0 ; i < li.size();i++ )
  {
   System.out.println(li.get(i));
  }
}

以上是“Java如何實現笛卡爾積算法”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！