溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
AVL樹
AVL樹又稱為高度平衡的二叉搜索樹,它能保持二叉樹的高度平衡,盡量降低二叉樹的高度,減少樹的平均搜索長度;
AVL樹的性質
左子樹和右子樹的高度之差的絕對值不超過1
樹中的每個左子樹和右子樹都是AVL樹
下面實現一棵AVL樹,主要實現其插入部分:
#pragma once
template <class K, class V>
struct AVLTreeNode
{
K _key;
V _val;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf;//平衡因子
AVLTreeNode(const K& key, const K& val)
:_key(key)
,_val(val)
,_left(NULL)
,_right(NULL)
,_parent(NULL)
,_bf(0)
{}
};
template <class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
AVLTree()
:_root(NULL)
{}
~AVLTree()
{
_Clear(_root);
}
bool Insert(const K& key, const V& val)
{
if(_root == NULL)//如果根結點為NULL,則創建一個結點,返回真
{
_root = new Node(key, val);
return true;
}
Node* cur = _root;
Node* prev = NULL;
while(cur != NULL)//查找合適的位置插入
{
if(cur->_key == key)//如果結點已存在,則返回假
return false;
else if(cur->_key > key)//如果要插入值小于當前結點,則去左子樹查找
{
prev = cur;
cur = cur->_left;
}
else//如果插入值大于當前結點,則去右子樹查找
{
prev = cur;
cur = cur->_right;
}
}
//循環結束,則表明找到了合適的位置,判斷應插入左邊還是右邊
Node* tmp = new Node(key, val);
if(key < prev->_key)
prev->_left = tmp;
else
prev->_right = tmp;
tmp->_parent = prev;
//插入結點之后,需要判斷當前樹是否滿足AVL樹的規則,若不滿足,進行相應的調整
while(prev != NULL)
{
//平衡因子為右邊高度減去左邊高度
if(prev->_left == tmp)
--(prev->_bf);
else
++(prev->_bf);
if(prev->_bf == 0)//如果平衡因子為0,則一定平衡,因為可以看做是在同一層插入了一個結點,對高度并無影響
break;
else if(prev->_bf == 1 || prev->_bf == -1)//如果平衡因子為1/-1,則表明高度有所變化,需要繼續向上調整
{
tmp = prev;
prev = prev->_parent;
}
else//說明平衡因子的絕對值大于1,則這個時候不滿足AVL樹的性質,需要進行調整
{
if(prev->_bf == 2)
{
if(tmp->_bf == 1)
_RotateL(prev);
else
{
_RotateR(tmp);
_RotateL(prev);
}
}
else
{
if(tmp->_bf == -1)
_RotateR(prev);
else
{
_RotateL(tmp);
_RotateR(prev);
}
}
break;
}
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout<<endl;
}
protected:
void _Clear(Node* root)
{
if(root != NULL)
{
_Clear(root->_left);
_Clear(root->_right);
delete root;
root = NULL;
}
}
//左單旋
void _RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if(subRL != NULL)
subRL->_parent = parent;
subR->_left = parent;
Node* ppNode = parent->_parent;
parent->_parent = subR;
if(ppNode == NULL)
_root = subR;
else
{
if(ppNode->_left == parent)
ppNode->_left = subR;
else
ppNode->_right = subR;
}
subR->_parent = ppNode;
parent->_bf = subR->_bf = 0;
}
//右單旋
void _RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR != NULL)
subLR->_parent = parent;
subL->_right = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
if(ppNode == NULL)
_root = subL;
else
{
if(ppNode->_left == parent)
ppNode->_left = subL;
else
ppNode->_right = subL;
}
subL->_parent = ppNode;
parent->_bf = subL->_bf = 0;
}
void _InOrder(Node* root)
{
if(root != NULL)
{
_InOrder(root->_left);
cout<<root->_key<<" ";
_InOrder(root->_right);
}
}
protected:
Node* _root;
};
void Test()
{
int arr[] = {4, 2, 6, 1, 3, 5, 15, 7, 16, 14};
//int arr[] = {16, 3, 7, 11, 9, 26, 18, 14, 15};
AVLTree<int, int> t;
for(int i = 0; i < sizeof(arr)/sizeof(arr[0]); ++i)
t.Insert(arr[i], i);
t.InOrder();
}其中的左右單旋如下圖所示:

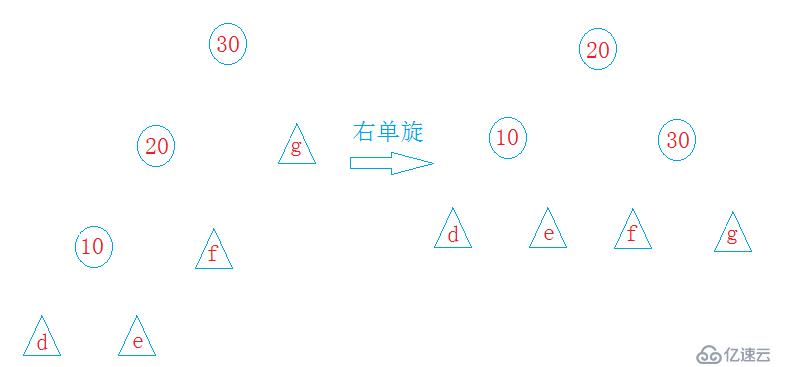
運行程序:

《完》
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。