您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
1、最小生成樹(MST樹)
針對連通圖;
(1)、現實意義:在n個城市之間建立通信網絡,連通n個城市,只需要n-1條線路;
但是n個城市之間共有 n*(n-1)/2條路線,如何選擇n-1條,使我們花費成本最小。
(2)、相同的一個圖形結構,有可能產生出不同形狀的生成樹,但是我們要找的是不同形狀生成樹里面耗費最小的一棵樹;
(3)、研究的問題:怎樣從生成樹里面找到花費代價最小的一顆,花費最小,成本最低;耗費代價最小的生成樹我們就稱之為:最小生成樹(MST樹)。
(4)、最小生成樹是不能有環形的;通過不同的方法,最終所找到的最小生成樹是相同的(在權值相同時,有可能不一樣,但是權值最小是唯一的,肯定的)。
2、Kruskal算法思想
思想:每次找權值最小的邊,與頂點關系不大(不關注頂點);
從邊的游離角度出發,每次都要找權值路徑最小的邊,(特別注意看所選的邊是否購成回路)
模型分析:
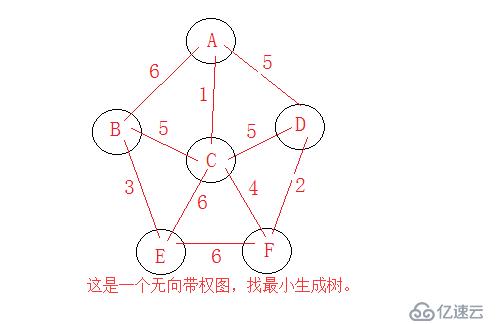
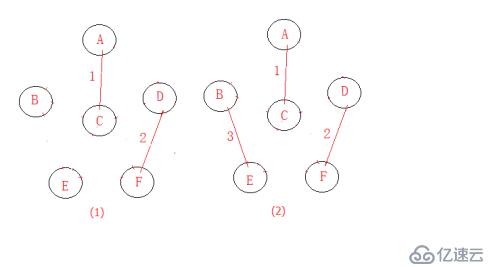
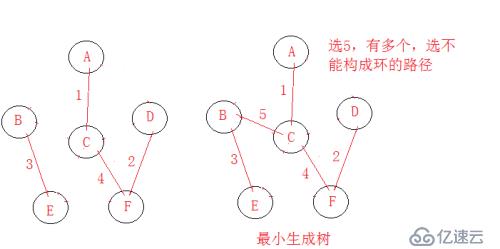
3、Kruskal算法實現
這里找最小代價cost時,采用的是數組(調用系統快排),當然用堆也可以。
均由C++代碼實現(用的是鄰接矩陣):
typedef struct MstEdge{ //最小生成樹的邊(弄成一個結構體)
int x; //row
int y; //col
int cost;
}MstEdge;
int cmp(const void *a, const void *b){ //快排比較的方法
return (*(MstEdge*)a).cost - (*(MstEdge*)b).cost;
}
bool isSame(int *father, int i, int j){ //判斷是否為回路,就是有相同的父節點
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
return i == j;
}
void markSame(int *father, int i, int j){ //連通之后,標記為有相同的父節點
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
father[j] = i;
}
template<typename Type, typename E>
void GraphMtx<Type, E>::MinSpanTree_Kruskal(){
int n = Graph<Type, E>::getCurVertex(); //由于要用到父類的保護數據或方法,有模板的存在,必須加上作用域限定符;
MstEdge *edge1 = new MstEdge[n*(n-1)/2]; //最小生成樹的數組
int k = 0;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
if(edge[i][j] != MAX_COST){
edge1[k].x = i;
edge1[k].y = j;
edge1[k].cost = edge[i][j];
k++;
}
}
}
qsort(edge1, k, sizeof(MstEdge), cmp); //調用系統的快排;
int *father = new int[n]; //弄一個父節點
Type v1, v2;
for(i = 0; i < n; i++){
father[i] = i; //自己的父就是自己頂點的下標
}
for(i = 0; i < n; i++){
if(!isSame(father, edge1[i].x, edge1[i].y)){ //父節點不相同
v1 = getValue(edge1[i].x);
v2 = getValue(edge1[i].y);
printf("%c-->%c : %d\n", v1, v2, edge1[i].cost); //找到了最小邊和cost
markSame(father, edge1[i].x, edge1[i].y); //標記為相同父節點;
}
}
}4、完整代碼、測試代碼、測試結果
(1)、完整代碼
#ifndef _GRAPH_H_
#define _GRAPH_H_
#include<iostream>
#include<queue>
using namespace std;
#define VERTEX_DEFAULT_SIZE 10
#define MAX_COST 0x7FFFFFFF
template<typename Type, typename E>
class Graph{
public:
bool isEmpty()const{
return curVertices == 0;
}
bool isFull()const{
if(curVertices >= maxVertices || curEdges >= curVertices*(curVertices-1)/2)
return true; //圖滿有2種情況:(1)、當前頂點數超過了最大頂點數,存放頂點的空間已滿
return false; //(2)、當前頂點數并沒有滿,但是當前頂點所能達到的邊數已滿
}
int getCurVertex()const{
return curVertices;
}
int getCurEdge()const{
return curEdges;
}
public:
virtual bool insertVertex(const Type &v) = 0; //插入頂點
virtual bool insertEdge(const Type &v1, const Type &v2, E cost) = 0; //插入邊
virtual bool removeVertex(const Type &v) = 0; //刪除頂點
virtual bool removeEdge(const Type &v1, const Type &v2) = 0; //刪除邊
virtual int getFirstNeighbor(const Type &v) = 0; //得到第一個相鄰頂點
virtual int getNextNeighbor(const Type &v, const Type &w) = 0; //得到下一個相鄰頂點
public:
virtual int getVertexIndex(const Type &v)const = 0; //得到頂點下標
virtual void showGraph()const = 0; //顯示圖
virtual Type getValue(int index)const = 0;
public:
virtual void DFS(const Type &v) = 0;
virtual void BFS(const Type &v) = 0;
protected:
int maxVertices; //最大頂點數
int curVertices; //當前頂點數
int curEdges; //當前邊數
};
template<typename Type, typename E>
class GraphMtx : public Graph<Type, E>{ //鄰接矩陣繼承父類矩陣
#define maxVertices Graph<Type, E>::maxVertices //因為是模板,所以用父類的數據或方法都得加上作用域限定符
#define curVertices Graph<Type, E>::curVertices
#define curEdges Graph<Type, E>::curEdges
public:
GraphMtx(int vertexSize = VERTEX_DEFAULT_SIZE){ //初始化鄰接矩陣
maxVertices = vertexSize > VERTEX_DEFAULT_SIZE ? vertexSize : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申請頂點空間
for(int i = 0; i < maxVertices; i++){ //都初始化為0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申請邊的行
for(i = 0; i < maxVertices; i++){ //申請列空間
edge[i] = new int[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //賦初值為0
for(int j = 0; j < maxVertices; j++){
if(i != j){
edge[i][j] = MAX_COST; //初始化時都賦為到其它邊要花的代價為無窮大。
}else{
edge[i][j] = 0; //初始化時自己到自己認為花費為0
}
}
}
curVertices = curEdges = 0; //當前頂點和當前邊數
}
GraphMtx(Type (*mt)[4], int sz){ //通過已有矩陣的初始化
int e = 0; //統計邊數
maxVertices = sz > VERTEX_DEFAULT_SIZE ? sz : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申請頂點空間
for(int i = 0; i < maxVertices; i++){ //都初始化為0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申請邊的行
for(i = 0; i < maxVertices; i++){ //申請列空間
edge[i] = new Type[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //賦初值為矩陣當中的值
for(int j = 0; j < maxVertices; j++){
edge[i][j] = mt[i][j];
if(edge[i][j] != 0){
e++; //統計列的邊數
}
}
}
curVertices = sz;
curEdges = e/2;
}
~GraphMtx(){}
public:
bool insertVertex(const Type &v){
if(curVertices >= maxVertices){
return false;
}
vertexList[curVertices++] = v;
return true;
}
bool insertEdge(const Type &v1, const Type &v2, E cost){
int maxEdges = curVertices*(curVertices-1)/2;
if(curEdges >= maxEdges){
return false;
}
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){
cout<<"edge no exit"<<endl; //要插入的頂點不存在,無法插入
return false;
}
if(edge[v][w] != MAX_COST){ //當前邊已經存在,不能進行插入
return false;
}
edge[v][w] = edge[w][v] = cost; //因為是無向圖,對稱, 權值賦為cost;
return true;
} //刪除頂點的高效方法
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
vertexList[i] = vertexList[curVertices-1];
int edgeCount = 0;
for(int k = 0; k < curVertices; k++){
if(edge[i][k] != 0){ //統計刪除那行的邊數
edgeCount++;
}
}
//刪除行
for(int j = 0; j < curVertices; j++){
edge[i][j] = edge[curVertices-1][j];
}
//刪除列
for(j = 0; j < curVertices; j++){
edge[j][i] = edge[j][curVertices-1];
}
curVertices--;
curEdges -= edgeCount;
return true;
}
/* //刪除頂點用的是數組一個一個移動的方法,效率太低。
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
for(int k = i; k < curVertices-1; ++k){
vertexList[k] = vertexList[k+1];
}
int edgeCount = 0;
for(int j = 0; j < curVertices; ++j){
if(edge[i][j] != 0)
edgeCount++;
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[k][j] = edge[k+1][j];
}
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[j][k] = edge[j][k+1];
}
}
curVertices--;
curEdges -= edgeCount;
return true;
}
*/
bool removeEdge(const Type &v1, const Type &v2){
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){ //判斷要刪除的邊是否在當前頂點內
return false; //頂點不存在
}
if(edge[v][w] == 0){ //這個邊根本不存在,沒有必要刪
return false;
}
edge[v][w] = edge[w][v] = 0; //刪除這個邊賦值為0,代表不存在;
curEdges--;
return true;
}
int getFirstNeighbor(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return -1;
}
for(int col = 0; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
int getNextNeighbor(const Type &v, const Type &w){
int i = getVertexIndex(v);
int j = getVertexIndex(w);
if(i==-1 || j==-1){
return -1;
}
for(int col = j+1; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
public:
void showGraph()const{
if(curVertices == 0){
cout<<"Nul Graph"<<endl;
return;
}
for(int i = 0; i < curVertices; i++){
cout<<vertexList[i]<<" ";
}
cout<<endl;
for(i = 0; i < curVertices; i++){
for(int j = 0; j < curVertices; j++){
if(edge[i][j] != MAX_COST){
cout<<edge[i][j]<<" ";
}else{
cout<<"@ ";
}
}
cout<<vertexList[i]<<endl;
}
}
int getVertexIndex(const Type &v)const{
for(int i = 0; i < curVertices; i++){
if(vertexList[i] == v){
return i;
}
}
return -1;
}
public:
Type getValue(int index)const{
return vertexList[index];
}
void DFS(const Type &v){
int n = Graph<Type, E>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
DFS(v, visit);
delete []visit;
}
void BFS(const Type &v){
int n = Graph<Type, E>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
queue<int> q; //隊列中存放的是頂點下標;
q.push(index);
int w;
while(!q.empty()){
index = q.front();
q.pop();
w = getFirstNeighbor(getValue(index));
while(w != -1){
if(!visit[w]){
cout<<getValue(w)<<"-->";
visit[w] = true;
q.push(w);
}
w = getNextNeighbor(getValue(index), getValue(w));
}
}
delete []visit;
}
public:
void MinSpanTree_Kruskal();
protected:
void DFS(const Type &v, bool *visit){
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
int w = getFirstNeighbor(v);
while(w != -1){
if(!visit[w]){
DFS(getValue(w), visit);
}
w = getNextNeighbor(v, getValue(w));
}
}
private:
Type *vertexList; //存放頂點的數組
int **edge; //存放邊關系的矩陣
};
//////////////////////////////////////////////////////////////////////////////////////////////////////
typedef struct MstEdge{
int x; //row
int y; //col
int cost;
}MstEdge;
int cmp(const void *a, const void *b){
return (*(MstEdge*)a).cost - (*(MstEdge*)b).cost;
}
bool isSame(int *father, int i, int j){
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
return i == j;
}
void markSame(int *father, int i, int j){
while(father[i] != i){
i = father[i];
}
while(father[j] != j){
j = father[j];
}
father[j] = i;
}
template<typename Type, typename E>
void GraphMtx<Type, E>::MinSpanTree_Kruskal(){
int n = Graph<Type, E>::getCurVertex(); //由于要用到父類的保護數據或方法,有模板的存在,必須加上作用域限定符;
MstEdge *edge1 = new MstEdge[n*(n-1)/2];
int k = 0;
for(int i = 0; i < n; i++){
for(int j = i+1; j < n; j++){
if(edge[i][j] != MAX_COST){
edge1[k].x = i;
edge1[k].y = j;
edge1[k].cost = edge[i][j];
k++;
}
}
}
qsort(edge1, k, sizeof(MstEdge), cmp);
int *father = new int[n];
Type v1, v2;
for(i = 0; i < n; i++){
father[i] = i;
}
for(i = 0; i < n; i++){
if(!isSame(father, edge1[i].x, edge1[i].y)){
v1 = getValue(edge1[i].x);
v2 = getValue(edge1[i].y);
printf("%c-->%c : %d\n", v1, v2, edge1[i].cost);
markSame(father, edge1[i].x, edge1[i].y);
}
}
}
#endif(2)、測試代碼
#include"Graph2.h"
int main(void){
GraphMtx<char,int> gm;
gm.insertVertex('A'); //0
gm.insertVertex('B'); //1
gm.insertVertex('C'); //2
gm.insertVertex('D'); //3
gm.insertVertex('E'); //4
gm.insertVertex('F'); //5
gm.insertEdge('A','B',6);
gm.insertEdge('A','C',1);
gm.insertEdge('A','D',5);
gm.insertEdge('B','C',5);
gm.insertEdge('B','E',3);
gm.insertEdge('C','E',6);
gm.insertEdge('C','D',5);
gm.insertEdge('C','F',4);
gm.insertEdge('D','F',2);
gm.insertEdge('E','F',6);
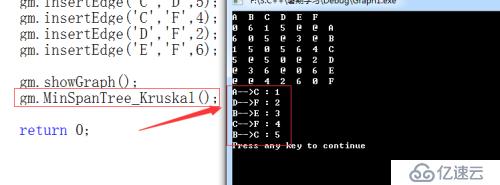
gm.showGraph();
gm.MinSpanTree_Kruskal();
return 0;
}(3)、測試結果
測試圖模型
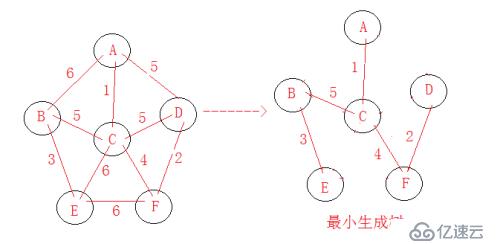
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。