數據結構-- 遞歸 排序

一.遞歸

一.遞歸的介紹
遞歸是一種數學上分而自治的思想
A.將原問題分解為規模較小的問題進行處理
1.分解后的問題與原問題的類型完全相同，但是規模較小
2.通過小規模問題的解，能夠輕易求得原問題的解
B.問題的分解時有限的(遞歸不能無限進行)
1.當邊界條件不滿足時，分解問題(遞歸繼續進行)
2.當邊界條件滿足時，直接求解(遞歸結束)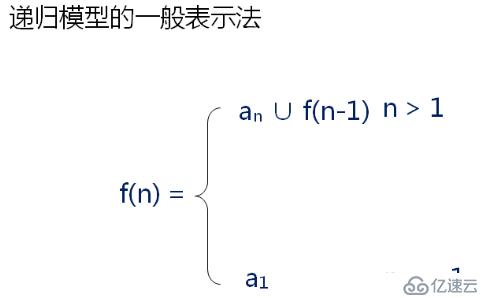

C.遞歸在程序設計中的應用
a.遞歸函數
1.函數體中存在自我調用的函數
2.遞歸函數必須有遞歸出口(邊界條件)
3.函數的無限遞歸將導致程序崩潰
示例:

int sum(unsigned int n)
{
    int ret;

    if(n==1)
    {
        ret=1;
    }
    if(n>1)
    {
        ret=n+sum(n-1);
    }

    return ret;
}

int fac(unsigned int n)
{
    if(n>=3)
    {
        return fac(n-1)+fac(n-2);
    }
    if((n==1)||(n==2))
    {
        return 1;
    }

    return 0;
}

二.遞歸的應用
單向鏈表的轉置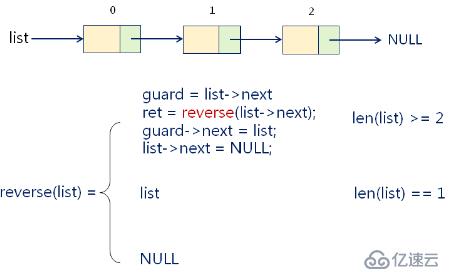

struct Node
{
    int data;
    Node* next;
};

Node* creat(int v,int len)
{
    Node* ret=NULL;
    Node* slider=NULL;

    for(int i=0;i<len;i++)
    {
        Node* n=new Node();

        n->data=v++;
        n->next=NULL;

        if(slider==NULL)
        {
            slider=n;
            ret=n;
        }
        else
        {
            slider->next=n;
            slider=n;
        }
    }

    return ret;
}

void destroy(Node* list)
{
    while(list)
    {
        Node* del=list;
        list=list->next;
        delete del;
    }
}

void print(Node* list)
{
    while(list)
    {
        cout<<list->data<<"->";
        list=list->next;
    }
    cout<<"NULL"<<endl;
}

Node* reserve(Node* list)//遞歸的實現
{
    Node* ret=NULL;
    if((list==NULL)||(list->next==NULL))
    {
        ret=list;
    }
    else
    {
        Node* guad=list->next;
        ret=reserve(list->next);
        guad->next=list;
        list->next=NULL;
    }
    return ret;
}

單向排序鏈表的合并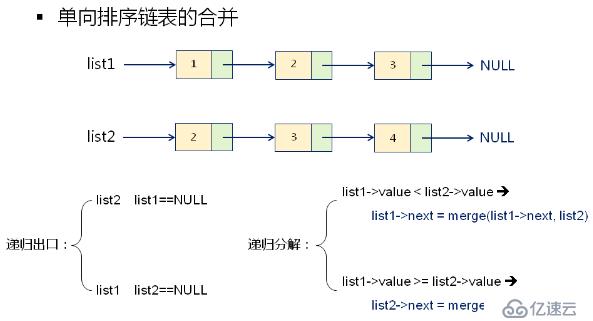

Node* merge(Node* list1, Node* list2)
{
  Node* ret = NULL;
  if(NULL == list1)
  {
    ret = list2;
  }
  else if(NULL == list2)
  {
    ret = list1;
  }
  else if(list1->data < list2->data)
  {
    list1->next = merge(list1->next,list2);
    ret = list1;
  }
  else
  {
    list2->next = merge(list2->next, list1);
    ret = list2;
  }
  return ret;
}

二.排序

排序的一般定義
排序時計算機內經常進行的一種操作，其目的是將一組無序的數據元素調整為有序的數據元素

排序的數學定義
假設含n個數據元素的序列為{R1,R2....Rn}其相應的關鍵字序列為{K1,K2....，Kn},這些關鍵字相互之間可以進行比較，即:在它們之間存在一個關系:Kp1<=Kp2......<=Kpn，將此固有關系將上式記錄序列重新排列為{Rp1,Rp2....,Rpn}的操作稱為排序
排序的穩定性
如果在序列中有兩個元素r[i]和r[j]，它們的關鍵字K[i]==K[j],且在排序之前，對象r[i]排在r[j]前面；如果在排序之后，對象r[i]仍在r[j]的前面，則稱這個排序方法是穩定的，否則稱這個排序方法是不穩定的
排序的審判
時間性能
1.關鍵性能差異體現在比較和交換的數量
輔助存儲空間‘
1.為完成排序操作需要的額外的存儲空間
2.必要時可以“空間換時間”
算法的實現復雜性
1.過于復雜的排序法可能影響可讀性和維護性
各種排序的實現
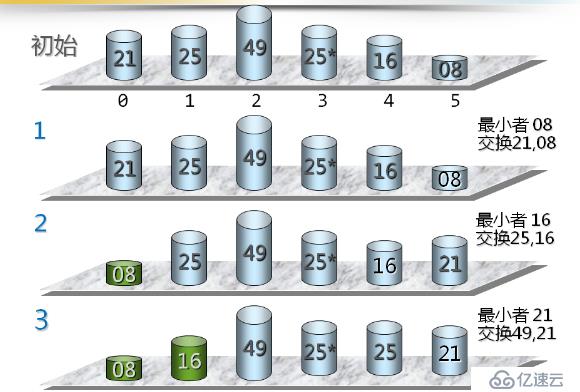
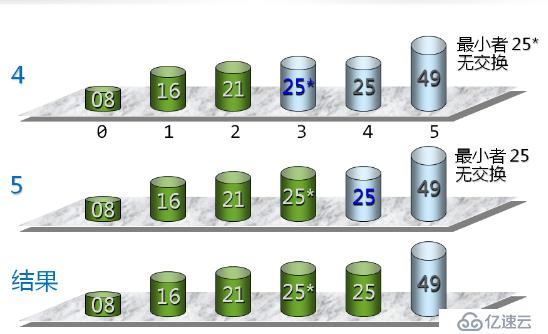
A.選擇排序的基本思想
每次(例如第i次,i=o,1,......n-2)從后面n-i個待排的數據元素中選出關鍵字最小的元素，作為有序元素序列第i個元素
圖示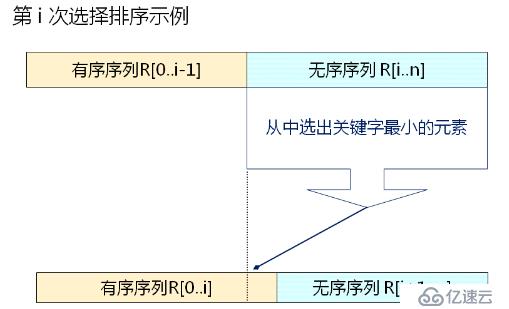

 template <typename T>
        static void select(T array[],int len)
        {
            for(int i=0;i<len;i++)
            {
                int min=i;//從第i個元素開始

                for(int j=i+1;j<len;j++)//將最小值與剩下的元素進行比較
                {
                    if(array[min]>array[j])
                    {
                        min=j;
                    }
                }
                if(min!=i)
                {
                    Swap(array[i],array[min]);

                }
                //Swap(arrar[0],arrar[min]);
            }
         }

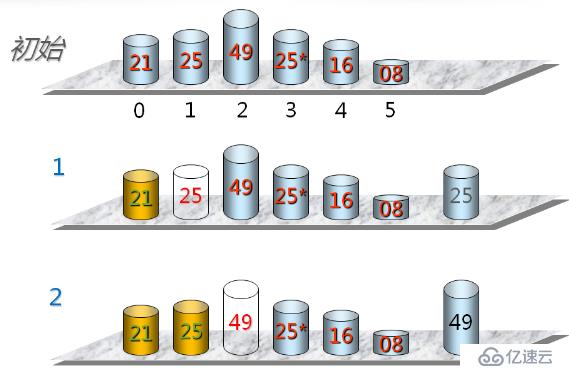
插入排序的基本思想
當插入第i(i>=1)個數據元素時，前面的V[0],V[1],...,V[i-1]已經排好序，這時，用V[i]的關鍵字與V[i-1],V[i-2],...,V[0]關鍵字進行比較，找到位置后將V[i]插入，原來位置上的對象向后順移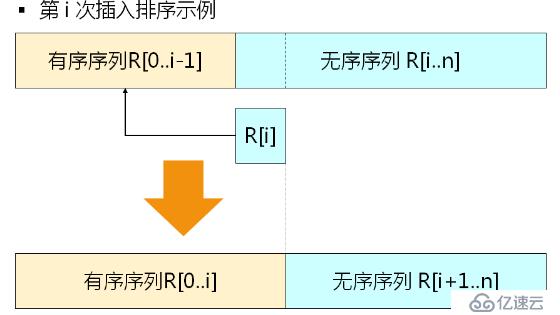

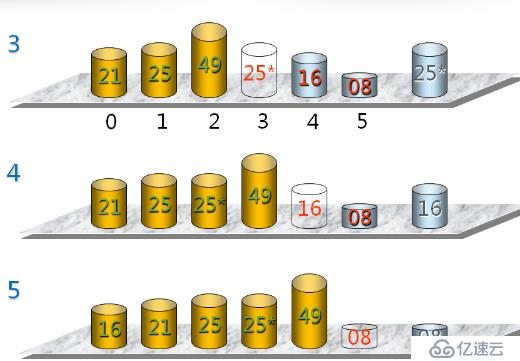
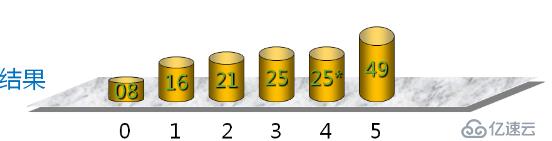
 template <typename T>
         static void insert(T array[],int len)
         {
             for(int i=0;i<len;i++)
             {
                 int k=i;
                 T temp=array[i];
                 for(int j=i-1;j>=0;j--)
                 {
                     if(array[j]>temp)//如果array[j]下的值大于temp,將array[j]往后移動一位
                     {
                        array[j+1]=array[j];
                        k=j;
                     }
                     else
                     {
                         break;
                     }
                 }
                 if(k!=i)
                 {
                     array[k]=temp;
                 }
             }
         }

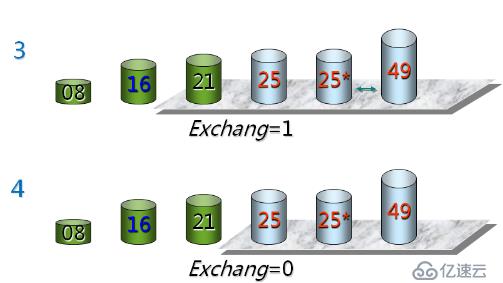
冒泡排序的基本思想
每次從后向前進行(假設為第i次),j=n-1,n-1,...,i,兩兩比較V[j-1]和V[j]的關鍵字；如果發生逆序，則交換V[j-1]和V[j]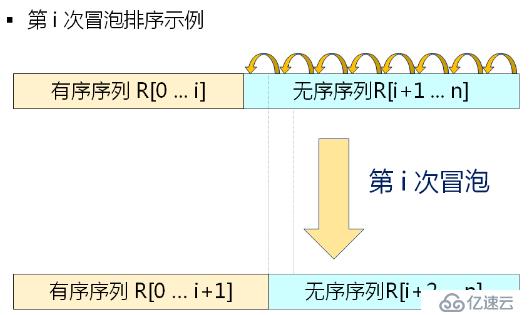

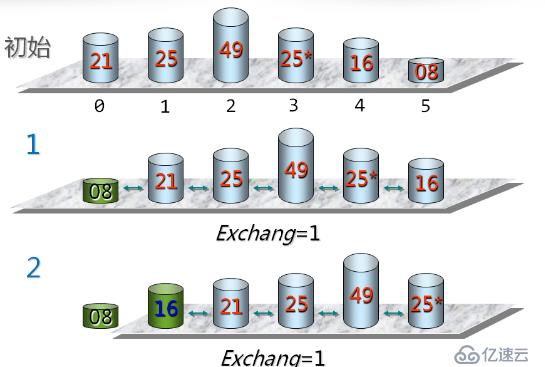
         template <typename T>//冒泡排序
         static void Bubble(T array[],int len)
         {
             bool exchange=true;
             for(int i=0;(i<len)&&exchange;i++)//從后往前的實現
             {
                 exchange=false;

                 for(int j=len-1;j>i;j--)
                 {
                     if(array[j]<array[j-1])
                     {
                        Swap(array[j-1],array[j]);
                     }
                 }
             }
         }

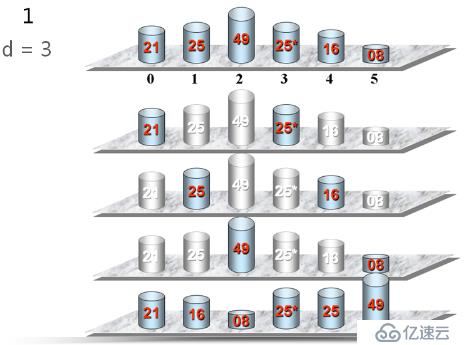
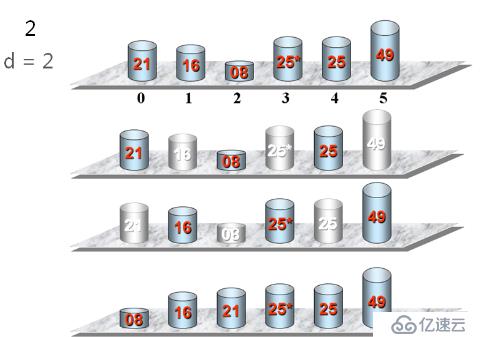
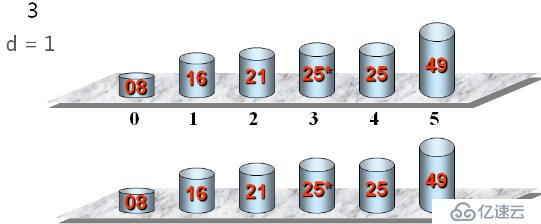
希爾排序的基本思想
將待排序列劃分為若干組，在每一組內進行插入排序，以使整個序列基本有序，然后再對整個序列進行插入排序

        template <typename T>
         static void Shell(T array[],int len)
         {
             int d=len;

             do
             {
                d=d/3+1;//d為增量 d的值在排序的過程中由大到小逐漸縮小，直至最后一趟排序減為1

                for(int i=d;i<len;i+=d)
                {
                    //cout<<i;
                    int k=i;
                    T temp=array[i];
                    for(int j=i-d;j>=0;j-=d)
                    {
                        if(array[j]>temp)
                        {
                           array[j+d]=array[j];
                           k=j;
                           //cout<<k;
                        }
                        else
                        {
                            break;
                        }
                    }
                    if(k!=i)
                    {
                        array[k]=temp;
                    }
                }
             }while(d>1);
         }

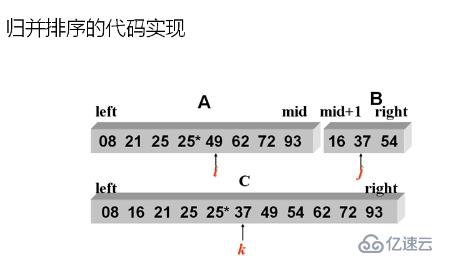
歸并排序的基本思想
將兩個或兩個以上的有序序列合并成一個新的有序序列
有序序列V[0]...V[m]和V[m+1]....V[n-1]====>V[0]...V[n-1]這種歸并方法稱為2路歸并
歸并的套路
1.將3個有序序列歸并為一個新的有序序列，稱為3路歸并
2.將N個有序序列歸并為一個新的有序序列，稱為N路歸并
3.將多個有序序列歸并為一個新的有序序列，稱為多路歸并

         template <typename T>//歸并排序的實現
         static void Merge(T array[],int len)
         {
             T* helper=new T[len];//申請的輔助空間

             if(helper!=NULL)
             {
                 Merge(array,helper,0,len-1);
             }
         }

                template <typename T>
        static void Merge(T src[],T helper[],int begin,int mid,int end)
        {
            int i=begin;
            int j=mid+1;
            int k=begin;

            while((i<=mid)&&(j<=end))
            {
                if(src[i]<src[j])
                {
                    helper[k++]=src[i++];
                }
                else
                {
                    helper[k++]=src[j++];
                }
            }

            while(i<=mid)
            {
                helper[k++]=src[i++];
            }
            while(j<=end)
            {
                helper[k++]=src[j++];
            }

            for(i=begin;i<=end;i++)
            {
                src[i]=helper[i];
            }
        }

        template <typename T>
        static void Merge(T src[],T helper[],int begin,int end)
        {
            if(begin==end)
            {
                return;
            }
            else
            {
                int mid=(begin+end)/2;

                Merge(src,helper,begin,mid);
                Merge(src,helper,mid+1,end);
                Merge(src,helper,begin,mid,end);
            }
        }

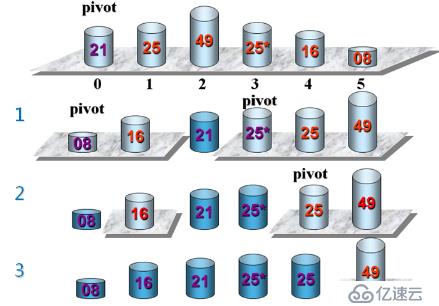
快速排序的基本思想
任取序列在的某個數據元素作為基準將整個序列劃分為左右兩個子序列
1.左側子序列在中所有元素都小于或等于基準元素
2.右側子序列中所有元素都大于基準元素
3.基準元素排在這兩個子序列中間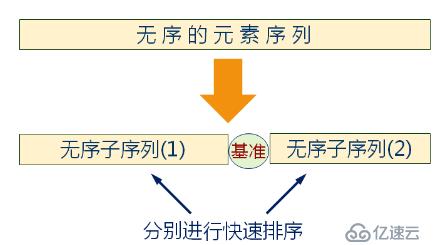

         template <typename T>//快速排序
         static void Quick(T array[],int len)
         {
             Quick(array,0,len-1);
         }

                 template <typename T>
        static int Partiton(T array[],int begin,int end)
        {
            T pv=array[begin];

            while(begin<end)
            {
                while((begin<end)&&(array[end]>pv))
                {
                    end--;
                }
                Swap(array[begin],array[end]);

                while((begin<end)&&(array[begin]<=pv))
                {
                    begin++;
                }
                Swap(array[begin],array[end]);
            }

            array[begin]=pv;

            return begin;
        }

        template <typename T>
        static void Quick(T array[],int begin,int end)
        {
            if(begin<end)
            {
                int pivot=Partiton(array,begin,end);

                Quick(array,begin,pivot-1);
                Quick(array,pivot+1,end);
            }
        }