您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
在數據排序的算法中,不同數據規模應當使用合適的排序算法才能達到最好的效果,如小規模的數據排序,可以使用冒泡排序、插入排序,選擇排序,他們的時間復雜度都為O(n2),大規模的數據排序就可以使用歸并排序和快速排序,時間復雜度為O(nlogn)。今天我們就來看一下歸并排序和快速排序。
排序數組,將數組從中間分成前后兩部分,對前后兩部分分別排序,然后合在一起,這個數組就是有序的。
1.歸并排序是一個穩定的排序算法:在合并的過程中,如果A[p...q]和A[q+1...r]之間中有相同的元素,先把A[p...q]中的元素放入tmp數組。這樣就保證了值相同的元素,在合并前后的先后順序不變。
2.歸并排序的時間復雜度是O(nlogn):在解決遞歸問題時,我們得出一個結論:遞歸問題可以寫成遞推公式,遞歸代碼的時間復雜度也可以寫成遞推公式
我們假設對n個元素進行歸并排序需要的時間是T(n),那分解成兩個子數組排序的時間都是T(n/2),套用結論可以得到歸并排序的時間復雜度的計算公式就是:
T(1) = C; n=1 時,只需要常量級的執行時間,所以表示為 C。 T(n) = 2*T(n/2) + n; n>1
再次將這個公式分解:
T(n) = 2*T(n/2) + n = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n ...... = 2^k * T(n/2^k) + k * n ......
我們可以得到T(n)=2^kT(n/2^k)+kn.當T(n/2^k)=T(1)時,也就是n/2^k=1,我們將得到k=log2n,問你將k帶入公式得到
T(n)=Cn+nlog2n
用大O標記法來表示為T(n) 就等于 O(nlogn)
而且時間復雜度是非常穩定的:最好情況,最壞情況,還是平均情況,時間復雜度都是O(nlogn)
3、歸并排序的空間復雜度為O(n)
歸并排序的致命缺點:歸并排序不是原地排序算法(在合并兩個有序數組時,需要借助額外的存儲空間)
遞歸代碼的空間復雜度并不能像時間復雜度那樣累加、盡管每次合并操作都需要申請額外的內存空間,但在合并完成之后、臨時開辟的內存空間就被釋放掉了、臨時內存空間最大也不會超過 n 個數據的大小
如果要排序數組中下標從p到r之間的一組數據,我們選擇p到r之間的任意一個數據作為pivot(分區點),遍歷數據,見小于pivot的放在右邊,大于pivot放在左邊。這樣數組就分成了三部分,用遞歸排序下標從 p 到 q-1 之間的數據和下標從 q+1.到r之間的數據,直到區間縮小為1,說明數據都有序
快速排序的時間復雜度為O(1):在排序過程中,假如遇到需要移動數據的,我們可以之間用交換的思想
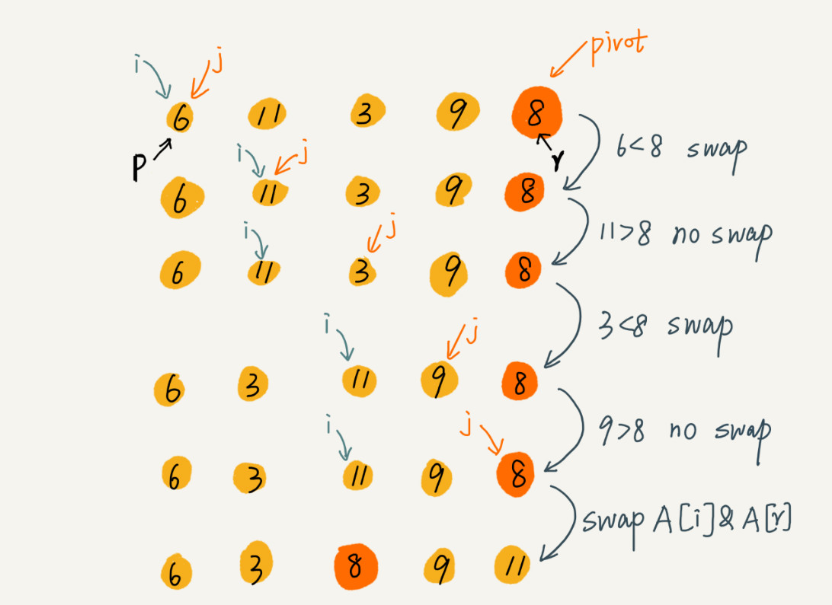
(圖片來源于網絡,侵刪)
空間復雜度為O(1)
看圖:
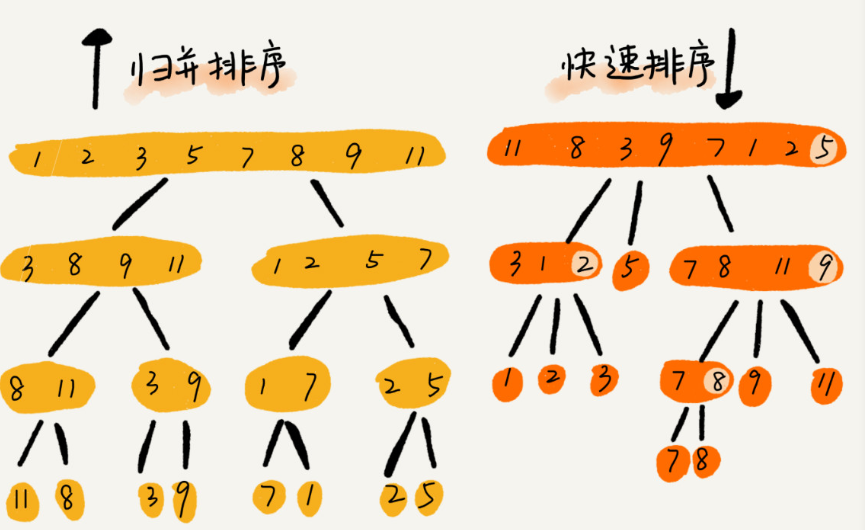
(圖片來源于網絡,侵刪)
處理過程的差異:
遞歸排序:先處理子問題再合并
快速排序:先分區,再處理子問題
歸并排序雖然穩定,是時間復雜度為O(nlogn)的排序算法,但是它不是原地排序算法,合并過程中需要額外的空間。
遞歸代碼的時間復雜度,如果每次分區操作,都能正好將數組分為兩個大小相等的兩個小區間,那快速排序的遞推公式和遞推排序是相同的,所以,快排的時間復雜度為O(nlogn)
但是,每次都分得那么均勻是非常難實現的。
T(n)在大部分情況下的時間復雜度都可以做到O(nlogn),只有在極端情況下才會退化為O(n2).
遞歸和快排都是分治的思想,代碼都通過遞歸來實現,過程非常相似。歸并排序時間復雜度都非常穩定為O(nlogn),但是每次合并的時候都需要額外的空間,空間復雜度非常高為是O(n),快速排序算法雖然最壞時間復雜度為O(n2),但是平均時間復雜度為O(nlogn),最壞的情況我們也可以避免。
數據結構與算法學習筆記之寫鏈表代碼的正確姿勢(下)
數據結構與算法學習筆記之 提高讀取性能的鏈表(上)
數據結構與算法學習筆記之 從0編號的數組
數據結構與算法學習筆記之后進先出的“桶”
數據結構與算法學習筆記之先進先出的隊列
數據結構與算法學習筆記之高效、簡潔的編碼技巧“遞歸”
以上內容為個人的學習筆記,僅作為學習交流之用。

歡迎大家關注公眾號,不定時干貨,只做有價值的輸出
作者:Dawnzhang
出處:https://www.cnblogs.com/clwydjgs/
小舟從此逝,江海寄余生。 --狐貍
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。