C語言典型題——求菲波那切數列第N項

菲波那切數列*

1.引入
斐波那契數列（Fibonacci sequence），又稱黃金分割數列、因數學家列昂納多·斐波那契（Leonardoda Fibonacci）以兔子繁殖為例子而引入，故又稱為“兔子數列”，指的是這樣一個數列：1、1、2、3、5、8、13、21、34、……在數學上，斐波納契數列以如下被以遞推的方法定義：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在現代物理、準晶體結構、化學等領域，斐波納契數列都有直接的應用，為此，美國數學會從1963年起出版了以《斐波納契數列季刊》為名的一份數學雜志，用于專門刊載這方面的研究成果。

2.定義
斐波那契數列指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368
........這個數列從第3項開始，每一項都等于前兩項之和。
斐波那契數列的定義者，是意大利數學家列昂納多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍貫是比薩。他被人稱作“比薩的列昂納多”。1202年，他撰寫了《算盤全書》（Liber Abacci）一書。他是第一個研究了印度和阿拉伯數學理論的歐洲人。他的父親被比薩的一家商業團體聘任為外交領事，派駐地點于阿爾及利亞地區，列昂納多因此得以在一個阿拉伯老師的指導下研究數學。他還曾在埃及、敘利亞、希臘、西西里和普羅旺斯等地研究數學。
3.求解

1. 遞歸方法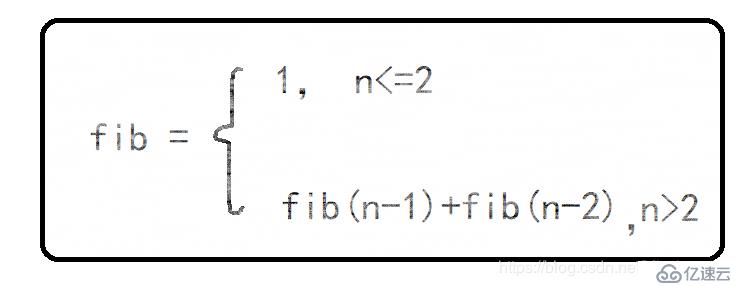

根據這個公式，應用遞歸調用可以很好的求解菲波那切數列第N項，以下為求解過程（源代碼）：

#include<stdio.h>
#include<stdlib.h>
int fib(int n)
{
    if (n <= 2)
        return  1;
    else 
        return  fib(n - 1) + fib(n - 2);
}
int main()
{
    int n = 0;
    int ret = 0;

    scanf("%d",&n);
    ret = fib(n);
    printf("%d\n", ret);
    system("pause");

    return 0;
}

我們在驗證前幾個菲波那切數列都沒有問題，但是這樣就完了嗎？不，其實再往下走，比如給個50他就算不出來了。這是為什么呢，仔細想想就不難發現：原來每次遞歸調用都會把一個值重復算好多遍，我們用個例子來驗證一下：

#include<stdio.h>
#include<stdlib.h>
int count = 0;
int fib(int n)
{

    if (n == 3)
        count++;
    if (n <= 2)
        return  1;
    else 
        return  fib(n - 1) + fib(n - 2);
}
int main()
{
    int n = 0;
    int ret = 0;

    scanf("%d",&n);
    ret = fib(n);
    printf("%d\n", ret);
    printf("%d\n", count);
    system("pause");

    return 0;
}

這個代碼輸出結果為

這里我們定義一個全局變量count，這里只僅僅計算了fib(3)被重復計算的次數就已經這么大了，可想而知這個代碼輸入的N值一旦很大計算效率就會變得極其差，那么怎么解決這個問題呢，下面在引進一個方法：

2.非遞歸——迭代（即循環）

我們怎么做呢，就是這樣：前三個菲波那切數我們知道，我們可不可以利用迭代來計算后面的斐波那契數呢，顯然是可以的。我們可以這樣想：首先讓a=1,b=1我們讓c=a+b然后利用循環來交換a，b，c的值不就好了。可是如何實現呢，以下分享一下我的想法：

#include<stdio.h>
#include<stdlib.h>
int fib(int n)
{
    int a = 1;
    int b = 1;
    int c = 0;
    while (n > 2)
    {
        c = a + b;
        a = b;
        b = c;
        n--;
    }
    return c;
}
int main()
{
    int n = 0;
    int ret = 0;

    scanf("%d",&n);
    ret = fib(n);
    printf("%d\n", ret);
    system("pause");

    return 0;
}

這個思想可以這樣實現，可是又出現一個問題，當n太大時數存不下來，從而導致計算可能有點問題，所以還是需要大佬們來完善一下。可是這個的效率絕對比上面的遞歸方法要高很多，這個計算比較小的n還是挺快的。
這里我們看到有些問題可以用遞歸去做，但是不適用遞歸解決它，否則只會適得其反。希望在小伙伴們的評論區里找到更好的解決辦法哦。