您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇“python怎么實現PID和調參”文章的知識點大部分人都不太理解,所以小編給大家總結了以下內容,內容詳細,步驟清晰,具有一定的借鑒價值,希望大家閱讀完這篇文章能有所收獲,下面我們一起來看看這篇“python怎么實現PID和調參”文章吧。
例子: 假設一個水缸,需要最終控制水缸的水位永遠維持在1米的高度。
水位目標:T 當前水位:Tn 加水量:U 誤差:error error=T-Tn 比例控制系數:kp U = k_p * errorU=kp∗error initial: T=1; Tn=0.2, error=1-0.2=0.8; kp=0.4
T=1
Tn=0.2
error=1-0.2
kp=0.4
for t in range(1, 10):
U = kp * error
Tn += U
error = T-Tn
print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')
"""
t=1 | add 0.32000 => Tn=0.52000 error=0.48000
t=2 | add 0.19200 => Tn=0.71200 error=0.28800
t=3 | add 0.11520 => Tn=0.82720 error=0.17280
t=4 | add 0.06912 => Tn=0.89632 error=0.10368
t=5 | add 0.04147 => Tn=0.93779 error=0.06221
t=6 | add 0.02488 => Tn=0.96268 error=0.03732
t=7 | add 0.01493 => Tn=0.97761 error=0.02239
t=8 | add 0.00896 => Tn=0.98656 error=0.01344
t=9 | add 0.00537 => Tn=0.99194 error=0.00806
"""根據kp取值不同,系統最后都會達到1米,只不過kp大了達到的更快。不會有穩態誤差。 若存在漏水情況,在相同情況下,經過多次加水后,水位會保持在0.75不在再變化,因為當U和漏水量一致的時候將保持不變——即穩態誤差 U=k_p*error=0.1 => error = 0.1/0.4 = 0.25U=kp∗error=0.1=>error=0.1/0.4=0.25,所以誤差永遠保持在0.25
T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1
for t in range(1, 100):
U = kp * error
Tn += U - extra_drop
error = T-Tn
print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')
"""
t=95 | add 0.10000 => Tn=0.75000 error=0.25000
t=96 | add 0.10000 => Tn=0.75000 error=0.25000
t=97 | add 0.10000 => Tn=0.75000 error=0.25000
t=98 | add 0.10000 => Tn=0.75000 error=0.25000
t=99 | add 0.10000 => Tn=0.75000 error=0.25000
"""實際情況中,這種類似水缸漏水的情況往往更加常見
比如控制汽車運動,摩擦阻力就相當于是"漏水"
控制機械臂、無人機的飛行,各類阻力和消耗相當于"漏水"
所以單獨的比例控制,很多時候并不能滿足要求
比例+積分控制算法: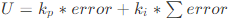
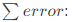 誤差累計
誤差累計
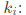 積分控制系數
積分控制系數
T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1
ki=0.2
sum_error = 0
for t in range(1, 20):
sum_error += error
U = kp * error + ki * sum_error
Tn += U - extra_drop
error = T-Tn
print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')
"""
t=14 | add 0.10930 => Tn=0.97665 error=0.02335
t=15 | add 0.11025 => Tn=0.98690 error=0.01310
t=16 | add 0.10877 => Tn=0.99567 error=0.00433
t=17 | add 0.10613 => Tn=1.00180 error=-0.00180
t=18 | add 0.10332 => Tn=1.00512 error=-0.00512
t=19 | add 0.10097 => Tn=1.00608 error=-0.00608
"""在越靠近目標的時候則加的越少。 
kd: 微分控制系數
d_error/d_t ~= error_t - error_t_1:誤差的變化
令:kd=0.2; d_error = 當前時刻誤差-前時刻誤差
T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1
ki=0.2
sum_error = 0
kd=0.2
d_error = 0
error_n = 0
error_b = 0
for t in range(1, 20):
error_b = error_n
error_n = error
# print(error_b1, error_b2)
d_error = error_n - error_b if t >= 2 else 0
sum_error += error
U = kp * error + ki * sum_error + kd * d_error
Tn += U - extra_drop
error = T-Tn
print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f} | d_error: {d_error:.5f}')
"""
t=14 | add 0.09690 => Tn=0.96053 error=0.03947 | d_error: 0.01319
t=15 | add 0.10402 => Tn=0.96455 error=0.03545 | d_error: 0.00310
t=16 | add 0.10808 => Tn=0.97263 error=0.02737 | d_error: -0.00402
t=17 | add 0.10951 => Tn=0.98214 error=0.01786 | d_error: -0.00808
t=18 | add 0.10899 => Tn=0.99113 error=0.00887 | d_error: -0.00951
t=19 | add 0.10727 => Tn=0.99840 error=0.00160 | d_error: -0.00899
"""

for kp_i in np.linspace(0, 1, 10): pid_plot(kp=kp_i, ki=0.2, kd=0.2)
for ki_i in np.linspace(0, 1, 10): pid_plot(kp=0.5, ki=ki_i, kd=0.2)
for kd_i in np.linspace(0, 1, 10): pid_plot(kp=0.5, ki=0.2, kd=kd_i)
pid_plot(kp=0.65, ki=0.05, kd=0.5, print_flag=True)
損失函數采用:RMSE
from scipy import optimize
import matplotlib.pyplot as plt
import numpy as np
def pid_plot(args, plot_flag=True, print_flag=False):
kp, ki, kd = args
T=1
Tn=0.2
error=1-0.2
extra_drop = 0.1
sum_error = 0
d_error = 0
error_n = 0
error_b = 0
Tn_list = []
for t in range(1, 100):
error_b = error_n
error_n = error
d_error = error_n - error_b if t >= 2 else 0
sum_error += error
U = kp * error + ki * sum_error + kd * d_error
Tn += U - extra_drop
error = T-Tn
Tn_list.append(Tn)
if print_flag:
print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f} | d_error: {d_error:.5f}')
if plot_flag:
plt.plot(Tn_list)
plt.axhline(1, linestyle='--', color='darkred', alpha=0.8)
plt.title(f'$K_p$={kp:.3f} $K_i$={ki:.3f} $K_d$={kd:.3f}')
plt.ylim([0, max(Tn_list) + 0.2])
plt.show()
loss = np.sqrt(np.mean(np.square(np.ones_like(Tn_list) - np.array(Tn_list))))
return loss
boundaries=[(0, 2), (0, 2), (0, 2)]
res = optimize.fmin_l_bfgs_b(pid_plot, np.array([0.1, 0.1, 0.1]), args=(False, False), bounds = boundaries, approx_grad = True)
pid_plot(res[0].tolist(), print_flag=True)
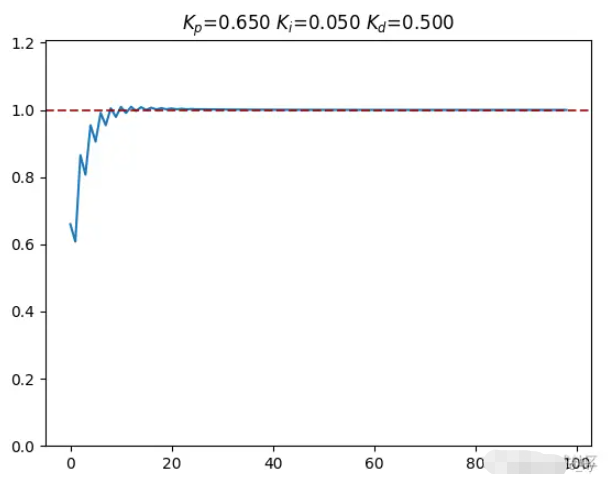
pid_plot([0.65, 0.05, 0.5], print_flag=True)牛頓法調參結果圖示 :
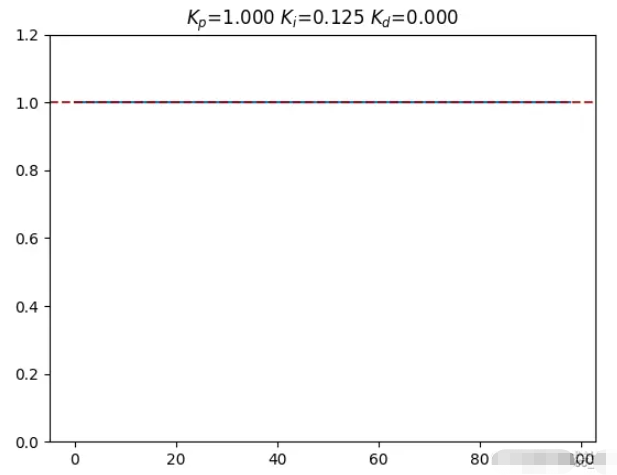
簡單手動調參圖示:
以上就是關于“python怎么實現PID和調參”這篇文章的內容,相信大家都有了一定的了解,希望小編分享的內容對大家有幫助,若想了解更多相關的知識內容,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。