您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下opencv傅里葉變換如何實現的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
圖像處理一般分為空間域處理和頻率域處理。
空間域處理是直接對圖像內的像素進行處理。
空間域處理主要劃分為灰度變換和空間濾波兩種形式。
灰度變換是對圖像內的單個像素進行處理,比如調節對比度和處理閾值等。
空間濾波涉及圖像質量的改變,例如圖像平滑處理。空間域處理的計算簡單方便,運算速度更快。
頻率域處理是先將圖像變換到頻率域,然后在頻率域對圖像進行處理,最后再通過反變換將圖像從頻率域變換到空間域。
時間差,在傅里葉變換里就是相位。相位表述的是與時間差相關的信息。
在圖像處理過程中,傅里葉變換就是將圖像分解為正弦分量和余弦分量兩部分,即將圖像從空間域轉換到頻域。
數字圖像經過傅里葉變換后,得到的頻域值是復數。因此,顯示傅里葉變換的結果需要使用實數圖像(real image)加虛數圖像(complex image),或者幅度圖像(magnitude image)加相位圖像(phase image)的形式。
因為幅度圖像包含了原圖像中我們所需要的大部分信息,所以在圖像處理過程中,通常僅使用幅度圖像。
如果希望先在頻域內對圖像進行處理,再通過逆傅里葉變換得到修改后的空域圖像,就必須同時保留幅度圖像和相位圖像。
對圖像進行傅里葉變換后,會得到圖像中的低頻和高頻信息。
低頻信息對應圖像內變化緩慢的灰度分量。高頻信息對應圖像內變化越來越快的灰度分量,是由灰度的尖銳過渡造成的。
傅里葉變換的目的,就是為了將圖像從空域轉換到頻域,并在頻域內實現對圖像內特定對象的處理,然后再對經過處理的頻域圖像進行逆傅里葉變換得到空域圖像。
傅里葉變換在圖像處理領域發揮著非常關鍵的作用,可以實現圖像增強、圖像去噪、邊緣檢測、特征提取、圖像壓縮和加密等。
Numpy模塊中的fft2()函數可以實現圖像的傅里葉變換。
Numpy提供的實現傅里葉變換的函數是numpy.fft.fft2(),它的語法格式是:
返回值 = numpy.fft.fft2(原始圖像)
參數“原始圖像”的類型是灰度圖像,函數的返回值是一個復數數組(complex ndarray)。
經過該函數的處理,就能得到圖像的頻譜信息。
此時,圖像頻譜中的零頻率分量位于頻譜圖像(頻域圖像)的左上角
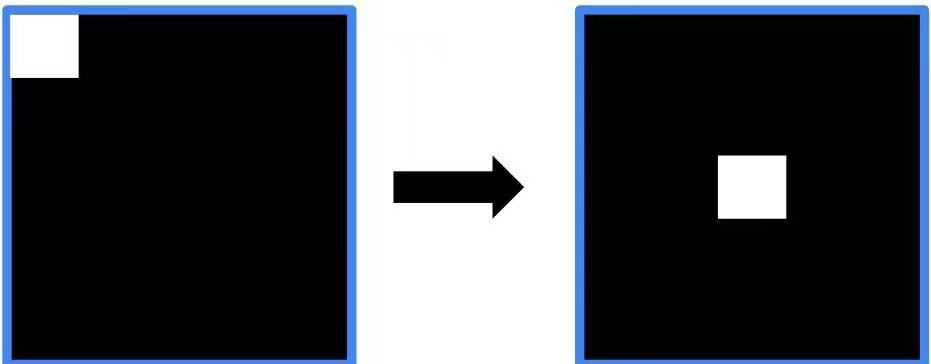
為了便于觀察,通常會使用numpy.fft.fftshift()函數將零頻率成分移動到頻域圖像的中心位置。
函數numpy.fft.fftshift()的語法格式是:
返回值=numpy.fft.fftshift(原始頻譜)
使用該函數處理后,圖像頻譜中的零頻率分量會被移到頻域圖像的中心位置,對于觀察傅里葉變換后頻譜中的零頻率部分非常有效。
對圖像進行傅里葉變換后,得到的是一個復數數組。
為了顯示為圖像,需要將它們的值調整到[0, 255]的灰度空間內,使用的公式為:
像素新值=20*np.log(np.abs(頻譜值))
用Numpy實現傅里葉變換,觀察得到的頻譜圖像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20*np.log(np.abs(fshift))
plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show()
注意: 如果在傅里葉變換過程中使用了numpy.fft.fftshift()函數移動零頻率分量,那么在逆傅里葉變換過程中,需要先使用numpy.fft.ifftshift()函數將零頻率分量移到原來的位置,再進行逆傅里葉變換
函數numpy.fft.ifftshift()是numpy.fft.fftshift()的逆函數,其語法格式為:
調整后的頻譜 = numpy.fft.ifftshift(原始頻譜)
numpy.fft.ifft2()函數可以實現逆傅里葉變換,返回空域復數數組。
它是numpy.fft.fft2()的逆函數,該函數的語法格式為:
返回值=numpy.fft.ifft2(頻域數據)
函數numpy.fft.ifft2()的返回值仍舊是一個復數數組(complex ndarray)。
逆傅里葉變換得到的空域信息是一個復數數組,需要將該信息調整至[0, 255]灰度空間內,使用的公式為:
iimg = np.abs(逆傅里葉變換結果)
在Numpy內實現傅里葉變換、逆傅里葉變換,觀察逆傅里葉變換的結果圖像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'), plt.axis('off')
plt.show()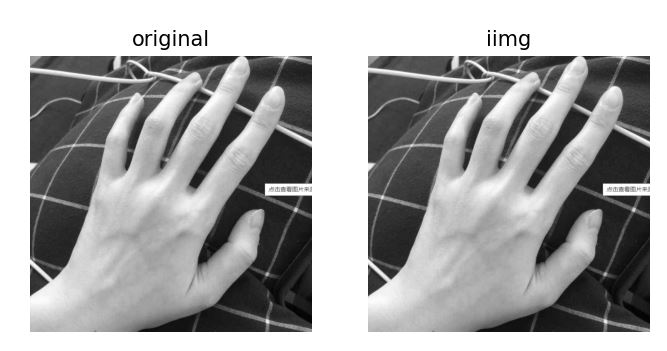
一幅圖像內,同時存在著高頻信號和低頻信號。
低頻信號對應圖像內變化緩慢的灰度分量。例如,在一幅大草原的圖像中,低頻信號對應著顏色趨于一致的廣袤草原。
高頻信號對應圖像內變化越來越快的灰度分量,是由灰度的尖銳過渡造成的。如果在上面的大草原圖像中還有一頭獅子,那么高頻信號就對應著獅子的邊緣等信息。
濾波器能夠允許一定頻率的分量通過或者拒絕其通過,按照其作用方式可以劃分為低通濾波器和高通濾波器。
允許低頻信號通過的濾波器稱為低通濾波器。低通濾波器使高頻信號衰減而對低頻信號放行,會使圖像變模糊。
允許高頻信號通過的濾波器稱為高通濾波器。高通濾波器使低頻信號衰減而讓高頻信號通過,將增強圖像中尖銳的細節,但是會導致圖像的對比度降低。
傅里葉變換可以將圖像的高頻信號和低頻信號分離。
通過對圖像的頻域處理,可以實現圖像增強、圖像去噪、邊緣檢測、特征提取、壓縮和加密等操作。
在Numpy內對圖像進行傅里葉變換,得到其頻域圖像。然后,在頻域內將低頻分量的值處理為0,實現高通濾波。最后,對圖像進行逆傅里葉變換,得到恢復的原始圖像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'), plt.axis('off')
plt.show()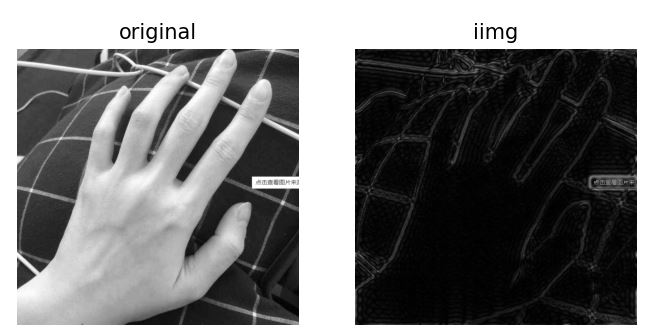
OpenCV提供了函數cv2.dft()和cv2.idft()來實現傅里葉變換和逆傅里葉變換
實現傅里葉變換
函數cv2.dft()的語法格式為:
返回結果=cv2.dft(原始圖像,轉換標識)
在使用該函數時,需要注意參數的使用規范:
對于參數“原始圖像”,要首先使用np.float32()函數將圖像轉換成np.float32格式。
“轉換標識”的值通常為“cv2.DFT_COMPLEX_OUTPUT”,用來輸出一個復數陣列。
函數cv2.dft()返回的結果與使用Numpy進行傅里葉變換得到的結果是一致的,但是它返回的值是雙通道的,第1個通道是結果的實數部分,第2個通道是結果的虛數部分。
經過函數cv2.dft()的變換后,得到了原始圖像的頻譜信息。
此時,零頻率分量并不在中心位置,為了處理方便需要將其移至中心位置,可以用函數numpy.fft.fftshift()實現。
例如,如下語句將頻譜圖像dft中的零頻率分量移到頻譜中心,得到了零頻率分量位于中心的頻譜圖像dftshift。
dftShift = np.fft.fftshift(dft)
經過上述處理后,頻譜圖像還只是一個由實部和虛部構成的值。要將其顯示出來,還要做進一步的處理才行。
函數cv2.magnitude()可以計算頻譜信息的幅度。該函數的語法格式為:
返回值=cv2.magnitude(參數1,參數2)
參數1:浮點型x坐標值,也就是實部。
參數2:浮點型y坐標值,也就是虛部,它必須和參數1具有相同的size
函數cv2.magnitude()的返回值是參數1和參數2的平方和的平方根,公式為:
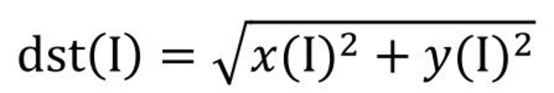
得到頻譜信息的幅度后,通常還要對幅度值做進一步的轉換,以便將頻譜信息以圖像的形式展示出來。簡單來說,就是需要將幅度值映射到灰度圖像的灰度空間[0, 255]內,使其以灰度圖像的形式顯示出來。
這里使用的公式為:
result = 20*np.log(cv2.magnitude(實部,虛部))
import numpy as np import cv2 img = cv2.imread('./img/hand1.jpg',0) dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT) print(dft) dftShift = np.fft.fftshift(dft) print(dftShift) result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1])) #兩個參數,需要拆分通道print(result)用OpenCV函數對圖像進行傅里葉變換,并展示其頻譜信息。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1]))
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()在OpenCV中,使用函數cv2.idft()實現逆傅里葉變換,該函數是傅里葉變換函數cv2.dft()的逆函數。其語法格式為:
返回結果=cv2.idft(原始數據)
對圖像進行傅里葉變換后,通常會將零頻率分量移至頻譜圖像的中心位置。如果使用函數numpy.fft.fftshift()移動了零頻率分量,那么在進行逆傅里葉變換前,要使用函數numpy.fft.ifftshift()將零頻率分量恢復到原來位置。
注意: 在進行逆傅里葉變換后,得到的值仍舊是復數,需要使用函數cv2.magnitude()計算其幅度。
用OpenCV函數對圖像進行傅里葉變換、逆傅里葉變換,并展示原始圖像及經過逆傅里葉變換后得到的圖像。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
ishift = np.fft.ifftshift(dftShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1]) # 計算幅度
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()在一幅圖像內,低頻信號對應圖像內變化緩慢的灰度分量。圖像進行低通濾波后會變模糊。

實現的中間步驟
rows, cols = img.shape crow, ccol = int(rows/2) , int(cols/2) mask = np.zeros((rows, cols,2), np.uint8) # 二維的原因,有實部和虛部 mask[crow-30:crow+30, ccol-30:ccol+30,:] = 1
然后,將其與頻譜圖像進行運算,實現低通濾波。這里采用的運算形式是:
fShift = dftShift*mask
使用函數cv2.dft()對圖像進行傅里葉變換,得到其頻譜圖像。然后,在頻域內將其高頻分量的值處理為0,實現低通濾波。最后,對圖像進行逆傅里葉變換,得到恢復的原始圖像。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('./img/hand1.png',0)
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
mask = np.zeros((rows, cols,2), np.uint8)
#兩個通道,與頻域圖像匹配
mask[crow-30:crow+30, ccol-30:ccol+30,:] = 1
fShift = dftShift*mask
ishift = np.fft.ifftshift(fShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()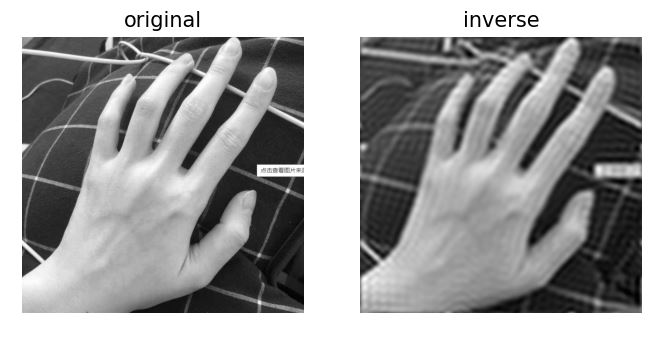
經過低通濾波后,圖像的邊緣信息被削弱了。
時域卷積 --> 頻域乘積
以上就是“opencv傅里葉變換如何實現”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。