您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“python機器學習GCN圖卷積神經網絡的原理是什么”,在日常操作中,相信很多人在python機器學習GCN圖卷積神經網絡的原理是什么問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”python機器學習GCN圖卷積神經網絡的原理是什么”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
圖卷積神經網絡涉及到圖信號處理的相關知識,也是由圖信號處理領域的知識推導發展而來,了解圖信號處理的知識是理解圖卷積神經網絡的基礎。
拉普拉斯矩陣是體現圖結構關聯的一種重要矩陣,是圖卷積神經網絡的一個重要部分。
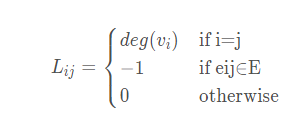
實例:

按照上述計算式子,可以得到拉普拉斯矩陣為:


1.1.3 拉普拉斯矩陣的性質

傅里葉變換是一種分析信號的方法,它可分析信號的成分,也可用這些成分合成信號。它將信號從時域轉換到頻域,從頻域視角給出了信號處理的另一種解法。(1)對于圖結構,可以定義圖上的傅里葉變換(GFT),對于任意一個在圖G上的信號x,其傅里葉變換表示為:

從線代角度,可以清晰的看出:v1,…, vn構成了N維特征空間中的一組完備基向量,G中任意一個圖信號都可表示為這些基向量的線性加權求和,系數為圖信號對應傅里葉基上的傅里葉系數。
回到之前提到的拉普拉斯矩陣刻畫平滑度的總變差:
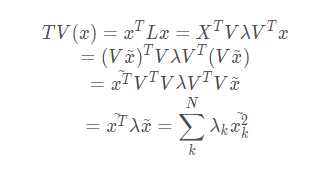
可以看成:刻畫圖平滑度的總變差是圖中所有節點特征值的線性組合,權值為傅里葉系數的平方。總變差取最小值的條件是圖信號與最小的特征值所對應的特征向量完全重合,結合其描述圖信號整體平滑度的意義,可將特征值等價成頻率:特征值越低,頻率越低,對應的傅里葉基變化緩慢,即相近節點的信號值趨于一致。
把圖信號所有的傅里葉系數結合稱為頻譜(spectrum),頻域的視角從全局視角既考慮信號本身,也考慮到圖的結構性質。
圖濾波器(Graph Filter)為對圖中的頻率分量進行增強或衰減,圖濾波算子核心為其頻率響應矩陣,為濾波器帶來不同的濾波效果。
故圖濾波器根據濾波效果可分為低通,高通和帶通。
低通濾波器:保留低頻部分,關注信號的平滑部分;
高通濾波器:保留高頻部分,關注信號的劇烈變化部分;
帶通濾波器:保留特定頻段部分;
而拉普拉斯矩陣多項式擴展可形成圖濾波器H:
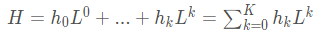
圖卷積運算的數學定義為:

上述公式存在一個較大問題:學習參數為N,這涉及到整個圖的所有節點,對于大規模數據極易發生過擬合。
進一步的化簡推導:將之前說到的拉普拉斯矩陣的多項式展開代替上述可訓練參數矩陣。

此結構內容即定義為圖卷積層(GCN layer),有圖卷積層堆疊得到的網絡模型即為圖卷積網絡GCN。
圖卷積層是對頻率響應矩陣的極大化簡,將本要訓練的圖濾波器直接退化為重歸一化拉普拉斯矩陣

優點:GCN作為近年圖神經網絡的基礎之作,對處理圖數據非常有效,其對圖結構的結構信息和節點的屬性信息同時學習,共同得到最終的節點特征表示,考慮到了節點之間的結構關聯性,這在圖操作中是非常重要的。
缺點:過平滑問題(多層疊加之后,節點的表示向量趨向一致,節點難以區分),由于GCN具有一個低通濾波器的作用(j聚合特征時使得節點特征不斷融合),多次迭代后特征會趨于相同。
GCN層的pytorch實現:
class GraphConvolutionLayer(nn.Module):
'''
圖卷積層:Lsym*X*W
其中 Lsym表示正則化圖拉普拉斯矩陣, X為輸入特征, W為權重矩陣, X'表示輸出特征;
*表示矩陣乘法
'''
def __init__(self, input_dim, output_dim, use_bias=True):
#初始化, parameters: input_dim-->輸入維度, output_dim-->輸出維度, use_bias-->是否使用偏置項, boolean
super(GraphConvolutionLayer,self).__init__()
self.input_dim=input_dim
self.output_dim=output_dim
self.use_bias=use_bias #是否加入偏置, 默認為True
self.weight=nn.Parameter(torch.Tensor(input_dim, output_dim))#權重矩陣為可訓練參數
if self.use_bias==True: #加入偏置
self.bias=nn.Parameter(torch.Tensor(output_dim))
else: #設置偏置為空
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
#初始化參數
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)#使用均勻分布U(-stdv,stdv)初始化權重Tensor
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)
def forward(self, adj, input_feature):
#前向傳播, parameters: adj-->鄰接矩陣(輸入為正則化拉普拉斯矩陣), input_future-->輸入特征矩陣
temp=torch.mm(input_feature, self.weight)#矩陣乘法, 得到X*W
output_feature=torch.sparse.mm(adj, temp)#由于鄰接矩陣adj為稀疏矩陣, 采用稀疏矩陣乘法提高計算效率, 得到Lsym*temp=Lsym*X*W
if self.use_bias==True: #若設置了偏置, 加入偏置項
output_feature+=self.bias
return output_feature定義兩層的GCN網絡模型:
class GCN(nn.Module): ''' 定義兩層GCN網絡模型 ''' def __init__(self, input_dim, hidden_dim, output_dim): #初始化, parameters: input_dim-->輸入維度, hidden_dim-->隱藏層維度, output_dim-->輸出維度 super.__init__(GCN, self).__init__() #定義兩層圖卷積層 self.gcn1=GraphConvolutionLayer(input_dim, hidden_dim) self.gcn2=GraphConvolutionLayer(hidden_dim, output_dim) def forward(self, adj, feature): #前向傳播, parameters: adj-->鄰接矩陣, feature-->輸入特征 x=F.relu(self.gcn1(adj, feature)) x=self.gcn2(adj, x) return F.log_softmax(x, dim=1)
到此,關于“python機器學習GCN圖卷積神經網絡的原理是什么”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。