您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“機器學習是什么”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
機器學習這個概念認為,對于待解問題,你無需編寫任何專門的程序代碼,泛型算法(generic algorithms)能夠在數據集上為你得出有趣的答案。對于泛型算法,不用編碼,而是將數據輸入,它將在數據之上建立起它自己的邏輯。
舉個例子,有一類算法稱為分類算法,它可以將數據劃分為不同的組別。一個用來識別手寫數字的分類算法,不用修改一行代碼,就可以用來將電子郵件分為垃圾郵件和普通郵件。算法沒變,但是輸入的訓練數據變了,因此它得出了不同的分類邏輯。
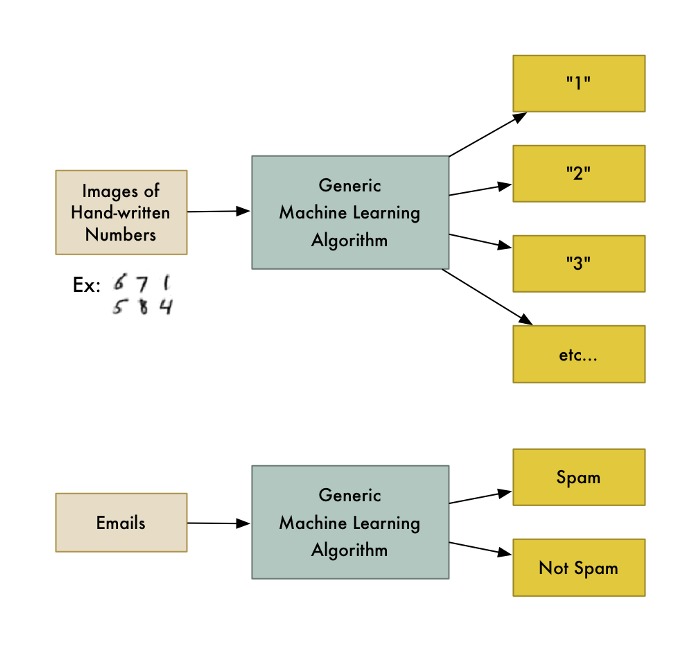
機器學習算法是個黑盒,可以重用來解決很多不同的分類問題。
“機器學習”是一個涵蓋性術語,覆蓋了大量類似的泛型算法。
你可以認為機器學習算法分為兩大類:監督式學習(Supervised Learning)和非監督式學習(Unsupervised Learning)。兩者區別很簡單,但卻非常重要。
假設你是一名房產經紀,生意越做越大,因此你雇了一批實習生來幫你。但是問題來了——你可以看一眼房子就知道它到底值多少錢,實習生沒有經驗,不知道如何估價。
為了幫助你的實習生(也許是為了解放你自己去度個假),你決定寫個小軟件,可以根據房屋大小、地段以及類似房屋的成交價等因素來評估你所在地區房屋的價值。
你把3個月來城里每筆房屋交易都寫了下來,每一單你都記錄了一長串的細節——臥室數量、房屋大小、地段等等。但最重要的是,你寫下了最終的成交價:
這是我們的“訓練數據”。

這就稱為監督式學習。你已經知道每一棟房屋的售價,換句話說,你知道問題的答案,并可以反向找出解題的邏輯。
為了編寫軟件,你將包含每一套房產的訓練數據輸入你的機器學習算法。算法嘗試找出應該使用何種運算來得出價格數字。
這就像是算術練習題,算式中的運算符號都被擦去了: 
即使你不是想去預測未知的數據(如價格),你也可以運用機器學習完成一些有意思的事。
這就有點像有人給你一張紙,上面列出了很多數字,然后對你說:“我不知道這些數字有什么意義,也許你能從中找出規律或是能將它們分類,或是其它什么-祝你好運!”
你該怎么處理這些數據呢?首先,你可以用個算法自動地從數據中劃分出不同的細分市場。也許你會發現大學附近的買房者喜歡戶型小但臥室多的房子,而郊區的買房者偏好三臥室的大戶型。這些信息可以直接幫助你的營銷。
你還可以作件很酷的事,自動找出房價的離群數據,即與其它數據迥異的值。這些鶴立雞群的房產也許是高樓大廈,而你可以將最優秀的推銷員集中在這些地區,因為他們的傭金更高。
本文余下部分我們主要討論監督式學習,但這并不是因為非監督式學習用處不大或是索然無味。實際上,隨著算法改良,不用將數據和正確答案聯系在一起,因此非監督式學習正變得越來越重要。
老學究請看:還有很多其它種類的機器學習算法。但初學時這樣理解不錯了。
作為人類的一員,你的大腦可以應付絕大多數情況,并且沒有任何明確指令也能夠學習如何處理這些情況。如果你做房產經紀時間很長,你對于房產的合適定價、它的最佳營銷方式以及哪些客戶會感興趣等等都會有一種本能般的“感覺”。強人工智能(Strong AI)研究的目標就是要能夠用計算機復制這種能力。
但是目前的機器學習算法還沒有那么好——它們只能專注于非常特定的、有限的問題。也許在這種情況下,“學習”更貼切的定義是“在少量范例數據的基礎上找出一個等式來解決特定的問題”。
不幸的是,“機器在少量范例數據的基礎上找出一個等式來解決特定的問題”這個名字太爛了。所以最后我們用“機器學習”取而代之。
當然,要是你是在50年之后來讀這篇文章,那時我們已經得出了強人工智能算法,而本文看起來就像個老古董。未來的人類,你還是別讀了,叫你的機器仆人給你做份三明治吧。
前面例子中評估房價的程序,你打算怎么寫呢?往下看之前,先思考一下吧。
如果你對機器學習一無所知,很有可能你會嘗試寫出一些基本規則來評估房價,如下:
Python
def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood): price = 0 # In my area, the average house costs $200 per sqft price_per_sqft = 200 if neighborhood == "hipsterton": # but some areas cost a bit more price_per_sqft = 400 elif neighborhood == "skid row": # and some areas cost less price_per_sqft = 100 # start with a base price estimate based on how big the place is price = price_per_sqft * sqft # now adjust our estimate based on the number of bedrooms if num_of_bedrooms == 0: # Studio apartments are cheap price = price?—?20000 else: # places with more bedrooms are usually # more valuable price = price + (num_of_bedrooms * 1000) return price
假如你像這樣瞎忙幾個小時,也許會取得一點成效,但是你的程序永不會完美,而且當價格變化時很難維護。
如果能讓計算機找出實現上述函數功能的辦法,這樣豈不更好?只要返回的房價數字正確,誰會在乎函數具體干了些什么呢?
def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood): price = <computer, plz do some math for me> return price
考慮這個問題的一種角度是將房價看做一碗美味的湯,而湯中成分就是臥室數、面積和地段。如果你能算出每種成分對最終的價格有多大影響,也許就能得到各種成分混合起來形成最終價格的具體比例。
這樣可以將你最初的程序(全是瘋狂的if else語句)簡化成類似如下的樣子:
def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood): price = 0 # a little pinch of this price += num_of_bedrooms * .841231951398213 # and a big pinch of that price += sqft * 1231.1231231 # maybe a handful of this price += neighborhood * 2.3242341421 # and finally, just a little extra salt for good measure price += 201.23432095 return price
請注意那些用粗體標注的神奇數字——.841231951398213, 1231.1231231,2.3242341421, 和201.23432095。它們稱為權重。如果我們能找出對每棟房子都適用的完美權重,我們的函數就能預測所有的房價!
找出最佳權重的一種笨辦法如下所示:
首先,將每個權重都設為1.0:
def estimate_house_sales_price(num_of_bedrooms, sqft, neighborhood): price = 0 # a little pinch of this price += num_of_bedrooms * 1.0 # and a big pinch of that price += sqft * 1.0 # maybe a handful of this price += neighborhood * 1.0 # and finally, just a little extra salt for good measure price += 1.0 return price
步驟2:
將每棟房產帶入你的函數運算,檢驗估算值與正確價格的偏離程度:
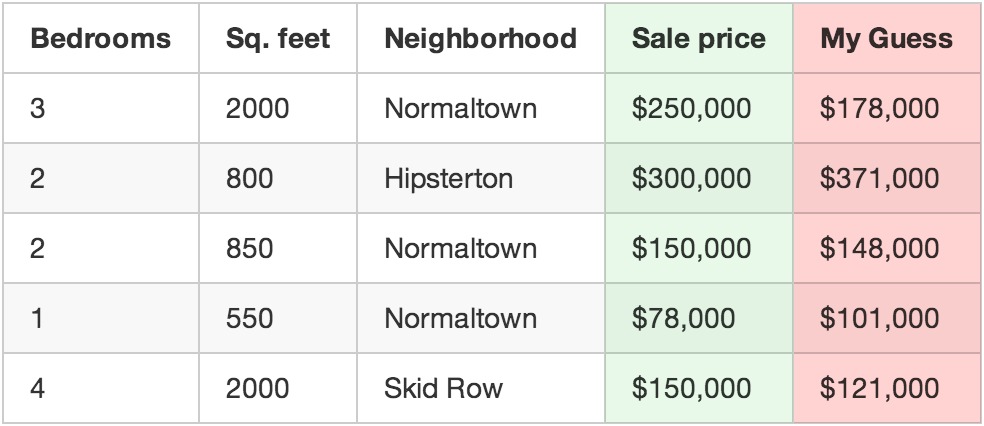
運用你的程序預測房屋價格。
例如:上表中第一套房產實際成交價為25萬美元,你的函數估價為17.8萬,這一套房產你就差了7.2萬。
再將你的數據集中的每套房產估價偏離值平方后求和。假設數據集中有500套房產交易,估價偏離值平方求和總計為86,123,373美元。這就反映了你的函數現在的“正確”程度。
現在,將總計值除以500,得到每套房產的估價偏離平均值。將這個平均誤差值稱為你函數的代價。
如果你能調整權重使得這個代價變為0,你的函數就完美了。它意味著,根據輸入的數據,你的程序對每一筆房產交易的估價都是分毫不差。而這就是我們的目標——嘗試不同的權重值以使代價盡可能的低。
不斷重復步驟2,嘗試所有可能的權重值組合。哪一個組合使得代價最接近于0,它就是你要使用的,你只要找到了這樣的組合,問題就得到了解決!
這太簡單了,對吧?想一想剛才你做了些什么。你取得了一些數據,將它們輸入至三個通用的簡單步驟中,最后你得到了一個可以對你所在區域的房屋進行估價的函數。房價網,要當心咯!
但是下面的事實可能會擾亂你的思想:
1.過去40年來,很多領域(如語言學/翻譯學)的研究表明,這種通用的“攪動數據湯”(我編造的詞)式的學習算法已經勝過了需要利用真人明確規則的方法。機器學習的“笨”辦法最終打敗了人類專家。
2.你最后寫出的函數真是笨,它甚至不知道什么是“面積”和“臥室數”。它知道的只是攪動,改變數字來得到正確的答案。
3.很可能你都不知道為何一組特殊的權重值能起效。所以你只是寫出了一個你實際上并不理解卻能證明的函數。
4.試想一下,你的程序里沒有類似“面積”和“臥室數”這樣的參數,而是接受了一組數字。假設每個數字代表了你車頂安裝的攝像頭捕捉的畫面中的一個像素,再將預測的輸出不稱為“價格”而是叫做“方向盤轉動度數”,這樣你就得到了一個程序可以自動操縱你的汽車了!
太瘋狂了,對吧?
好吧,當然你不可能嘗試所有可能的權重值來找到效果最好的組合。那可真要花很長時間,因為要嘗試的數字可能無窮無盡。
為避免這種情況,數學家們找到了很多聰明的辦法來快速找到優秀的權重值,而不需要嘗試過多。下面是其中一種:
首先,寫出一個簡單的等式表示前述步驟2:
這是你的代價函數。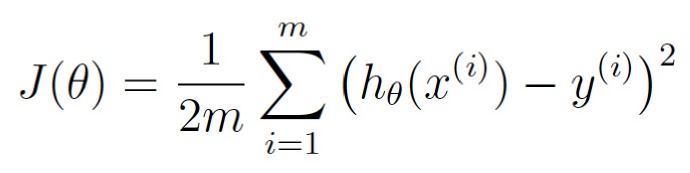
這個等式表示我們的估價程序在當前權重值下偏離程度的大小。
如果將所有賦給臥室數和面積的可能權重值以圖形形式顯示,我們會得到類似下圖的圖表:
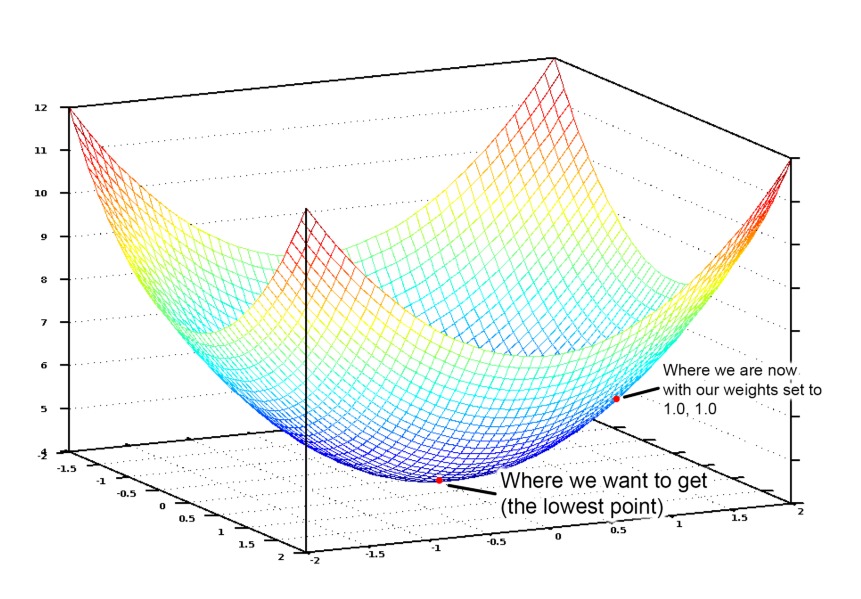
因此,我們只需要調整權重值使我們在圖上能向著最低點“走下坡路”。如果對于權重的細小調節能一直使我們保持向最低點移動,那么最終我們不用嘗試太多權重值就能到達那里。
如果你還記得一點微積分的話,你也許記得如果你對一個函數求導,結果會告訴你函數在任一點的斜率。換句話說,對于圖上給定一點,它告訴我們那條路是下坡路。我們可以利用這一點朝底部進發。
所以,如果我們對代價函數關于每一個權重求偏導,那么我們就可以從每一個權重中減去該值。這樣可以讓我們更加接近山底。一直這樣做,最終我們將到達底部,得到權重的最優值。(讀不懂?不用擔心,接著往下讀)。
這種找出最佳權重的辦法被稱為批量梯度下降,上面是對它的高度概括。如果想搞懂細節,不要害怕,繼續深入下去吧。
當你使用機器學習算法庫來解決實際問題,所有這些都已經為你準備好了。但明白一些具體細節總是有用的。
上面我描述的三步算法被稱為多元線性回歸。你估算等式是在求一條能夠擬合所有房價數據點的直線。然后,你再根據房價在你的直線上可能出現的位置用這個等式來估算從未見過的房屋的價格。這個想法威力強大,可以用它來解決“實際”問題。
但是,我為你展示的這種方法可能在簡單的情況下有效,它不會在所有情況下都有用。原因之一是因為房價不會一直那么簡單地跟隨一條連續直線。
但是,幸運的是,有很多辦法來處理這種情況。對于非線性數據,很多其他類型的機器學習算法可以處理(如神經網絡或有核向量機)。還有很多方法運用線性回歸更靈活,想到了用更復雜的線條來擬合。在所有的情況中,尋找最優權重值這一基本思路依然適用。
還有,我忽略了過擬合的概念。很容易碰上這樣一組權重值,它們對于你原始數據集中的房價都能完美預測,但對于原始數據集之外的任何新房屋都預測不準。這種情況的解決之道也有不少(如正則化以及使用交叉驗證數據集)。學會如何處理這一問題對于順利應用機器學習至關重要。
換言之,基本概念非常簡單,要想運用機器學習得到有用的結果還需要一些技巧和經驗。但是,這是每個開發者都能學會的技巧。
一旦你開始明白機器學習技術很容易應用于解決貌似很困難的問題(如手寫識別),你心中會有一種感覺,只要有足夠的數據,你就能夠用機器學習解決任何問題。只需要將數據輸入進去,就能看到計算機變戲法一樣找出擬合數據的等式。
但是很重要的一點你要記住,機器學習只能對用你占有的數據實際可解的問題才適用。
例如,如果你建立了一個模型來根據每套房屋內盆栽數量來預測房價,它就永遠不會成功。房屋內盆栽數量和房價之間沒有任何的關系。所以,無論它怎么去嘗試,計算機也推導不出兩者之間的關系。
你只能對實際存在的關系建模。
我認為,當前機器學習的最大問題是它主要活躍于學術界和商業研究組織中。對于圈外想要有個大體了解而不是想成為專家的人們,簡單易懂的學習資料不多。但是這一情況每一天都在改善。
吳恩達教授(Andrew Ng)在Coursera上的機器學習免費課程非常不錯。我強烈建議由此入門。任何擁有計算機科學學位、還能記住一點點數學的人應該都能理解。
另外,你還可以下載安裝SciKit-Learn,用它來試驗成千上萬的機器學習算法。它是一個python框架,對于所有的標準算法都有“黑盒”版本。
“機器學習是什么”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。