您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下Python+PuLP怎么實現線性規劃的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
如果您使用的是 Anaconda的話(事實上我也更推薦這樣做),需要先激活你想要安裝的虛擬環境,之后在 Prompt 輸入
pip install pulp
不出意外的話等一會就安裝完畢。
想必大家能點開這篇文章一定都知道線性規劃是什么意思吧……那么我用兩個例子再簡單說一下。
2.1.1 題目描述
若變量x,y 滿足約束條件:

求z=3x+y 的最大值。
2.1.2 基本概念
首先,我們要認清在這道題中,x和y是可以變的,所以把它們叫做決策變量。三個不等式叫做約束條件,即x和y必須同時滿足這三個不等式。我們若畫出圖來:
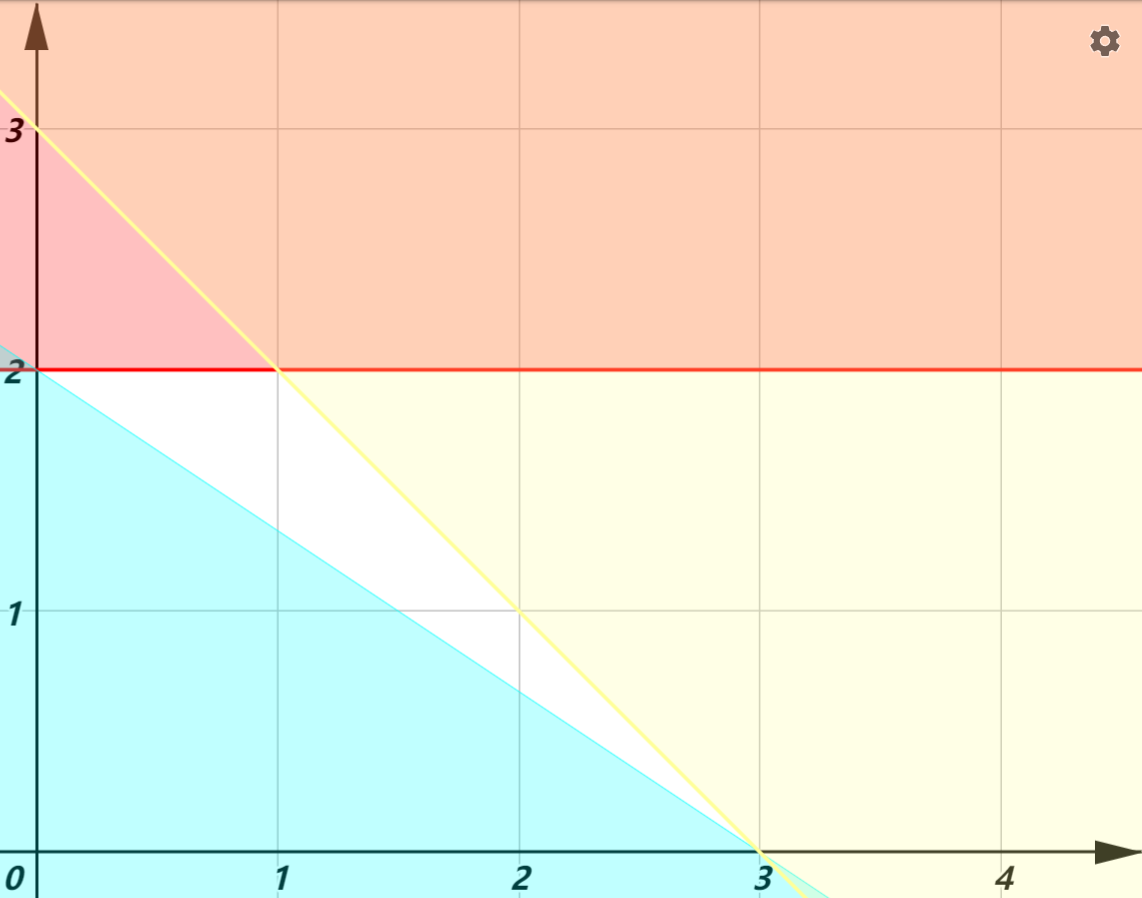
其中不滿足約束條件的區域被我標上了顏色,所以x,y 可以取得值只能在純白區域內,這一片區域稱作可行域。
再看最后的我們的目標:求z=x+3y 的最大值。
于是z=x+3y 就被稱作目標函數,我們的工作就是求這個目標函數的最大值。
整個問題描述為:

然后怎么算?別急我們再看一個例子。
2.2.1 題目描述
汽車廠生產小、中、大三種類型的汽車,已知各類型每輛車對鋼材、勞動時間的需求以及利潤如下表所示。要求每月的鋼材消耗不超過 600 t,總勞動時間不超過 60 000 h。試指定生產計劃使得工廠每月的利潤最大。
| 小型車 | 中型車 | 大型車 | |
|---|---|---|---|
| 鋼材 / t | 1.5 | 3 | 5 |
| 勞動時間 / h | 280 | 250 | 400 |
| 利潤 / 萬元 | 2 | 3 | 4 |
2.2.2 解題思路
首先,設三個決策變量,用x1,x2,x3 分別表示生產小型車、中型車、大型車的數量,但是注意要滿足:
車的數量只能是整數;
車的數量大于等于 0。
其他約束條件看題直接列:
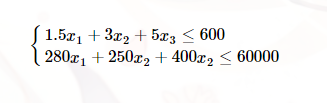
最后寫出目標函數:
z=2x1+3x2+4x3
綜合起來整個問題描述為:
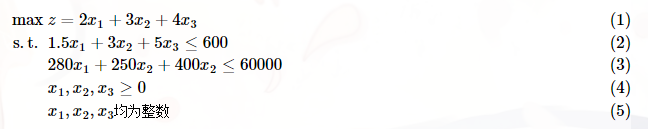
另外可以看出這個題由于涉及到三個決策變量,可行域是相當抽象的,這里就不畫了 hhh~
首先在最前面引入所需的pulp工具庫:
import pulp as pl
這句話是引入 pulp 庫并簡寫為 pl,一個 python 庫只有在開始 import 了之后才能在后面使用。這樣后面凡是用到 pulp 的功能都要寫成 pl.xxx。
接下來是以下幾個步驟:
定義模型
定義決策變量
添加約束條件
添加目標函數
模型求解
打印結果
# Define the model model = pl.LpProblem(name="My-Model", sense=pl.LpMaximize)
這個操作是使用 pl.LpProblem 創建了一個模型并賦值給變量 model,接收兩個參數:
name:模型的名字,隨便起一個;
sense:模型的類型,pl.LpMinimize是求目標函數的最小值,pl.LpMaximize 是求最大值
# Define the decision variables x = pl.LpVariable(name='x') y = pl.LpVariable(name='y')
如果你的變量比較少的話可以簡單這么寫。這個意思是定義了兩個浮點數變量,取值范圍是整個實數域。注意等號左邊的變量才是你在之后的計算式中使用的符號,而參數 name 只有在最后打印結果的時候才會被打印出來。另外如果你對變量有其他要求的話可以添加以下參數:
lowBound:變量的最小取值(不寫的話默認負無窮);
upBound:變量的最大取值(默認正無窮);
cat:變量的類型,有 pl.Binary 邏輯變量、pl.Integer 整數、pl.Continuous 實數(默認值);
如果你的變量比較多而不得不用 1, 2, 3…… 來編號,可以采用類似這樣的寫法:
# Define the decision variables
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 9)}這是一次定義 8 個變量并保存在一個類似數組的結構中,變量都是正整數,分別用 x[1],x[2], ..., x[8] 表示,依次命名為 x1, x2,..., x8。
注意 range(left, right) 表示的區間是左閉右開。
# Add constraints model += (2 * x + 3 * y - 6 >= 0, "constrain_1") model += (x + 3 * y - 3 == 0, "constrain_2")
沒錯!如你所見就是這么簡單,括號里第一個變量就是你的約束不等式或等式,第二個變量是你的自定義的約束名(可以起一個有意義的名字,當然也可以省略)。
由于一些比較數學的原因,約束條件里是不能使用大于號“>”或小于號“<”的。
如果你像前面一樣把變量定義在了數組中,那么可以直接用方括號調用:
model += (2 * x[1] + 3 * x[2] - 6 >= 0)
# Set the objective model += x + 3 * y
與前面添加約束條件不同,添加目標函數這一步不用加最外層的括號。
# Solve the optimization problem status = model.solve()
就寫這一句話,調用 model 的 solve() 方法,并把結果保存在 status 中。
# Get the results
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")然后你就能看到模型求解的結果了。
首先解決一下 3.1 的高考題:
import pulp as pl
# 定義一個模型,命名為 "Model_3.1",求最大值
model = pl.LpProblem(name="Model_3.1", sense=pl.LpMaximize)
# 定義兩個決策變量,取值為整個實數域
x = pl.LpVariable(name='x')
y = pl.LpVariable(name='y')
# 添加三個約束條件
model += (2 * x + 3 * y - 6 >= 0)
model += (x + y - 3 <= 0)
model += (y - 2 <= 0)
# 目標函數
model += x + 3 * y
# 求解
status = model.solve()
# 打印結果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")查看結果的最后幾行:
status: 1, Optimal
objective: 7.0
x: 1.0
y: 2.0
_C1: 2.0
_C2: 0.0
_C3: 0.0
最大值是7.0,在x=1.0,y=2.0 時取到。
import pulp as pl
# 定義一個模型,命名為 "Model_3.2",求最大值
model = pl.LpProblem(name="Model_3.2", sense=pl.LpMaximize)
# 定義三個決策變量,取值正整數
x = {i: pl.LpVariable(name=f"x{i}", lowBound=0, cat=pl.LpInteger) for i in range(1, 4)}
# 添加約束條件
model += (1.5 * x[1] + 3 * x[2] + 5 * x[3] <= 600)
model += (280 * x[1] + 250 * x[2] + 400 * x[3] <= 60000)
# 目標函數
model += 2 * x[1] + 3 * x[2] + 4 * x[3]
# 求解
status = model.solve()
# 打印結果
print(f"status: {model.status}, {pl.LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")
for var in model.variables():
print(f"{var.name}: {var.value()}")
for name, constraint in model.constraints.items():
print(f"{name}: {constraint.value()}")查看結果的最后幾行:
status: 1, Optimal
objective: 632.0
x1: 64.0
x2: 168.0
x3: 0.0
_C1: 0.0
_C2: -80.0
三種車的產量分別取 64、168、0,最大收益 632 萬元。
以上就是“Python+PuLP怎么實現線性規劃”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。