您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“java線性規劃問題舉例分析”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“java線性規劃問題舉例分析”吧!
由于我后臺是springcloud,所以我調查到兩種實現方式。
第一種是運用python的scipy開源庫寫一個python腳本,然后java后臺調用python腳本,求最優解,然后再將結果返回。
第二種是運用java中ibm組件Cplex直接求解,但分為收費和免費版,免費版決策變量限制為1000個,但也夠了。找jar包和dll費勁點。
發現他們倆算出來的最優解是相同的,但各個決策變量不太相同。
這里記錄一下運用java中ibm組件Cplex求解的方法。
首先看一下官方說明,免費版本的限制。
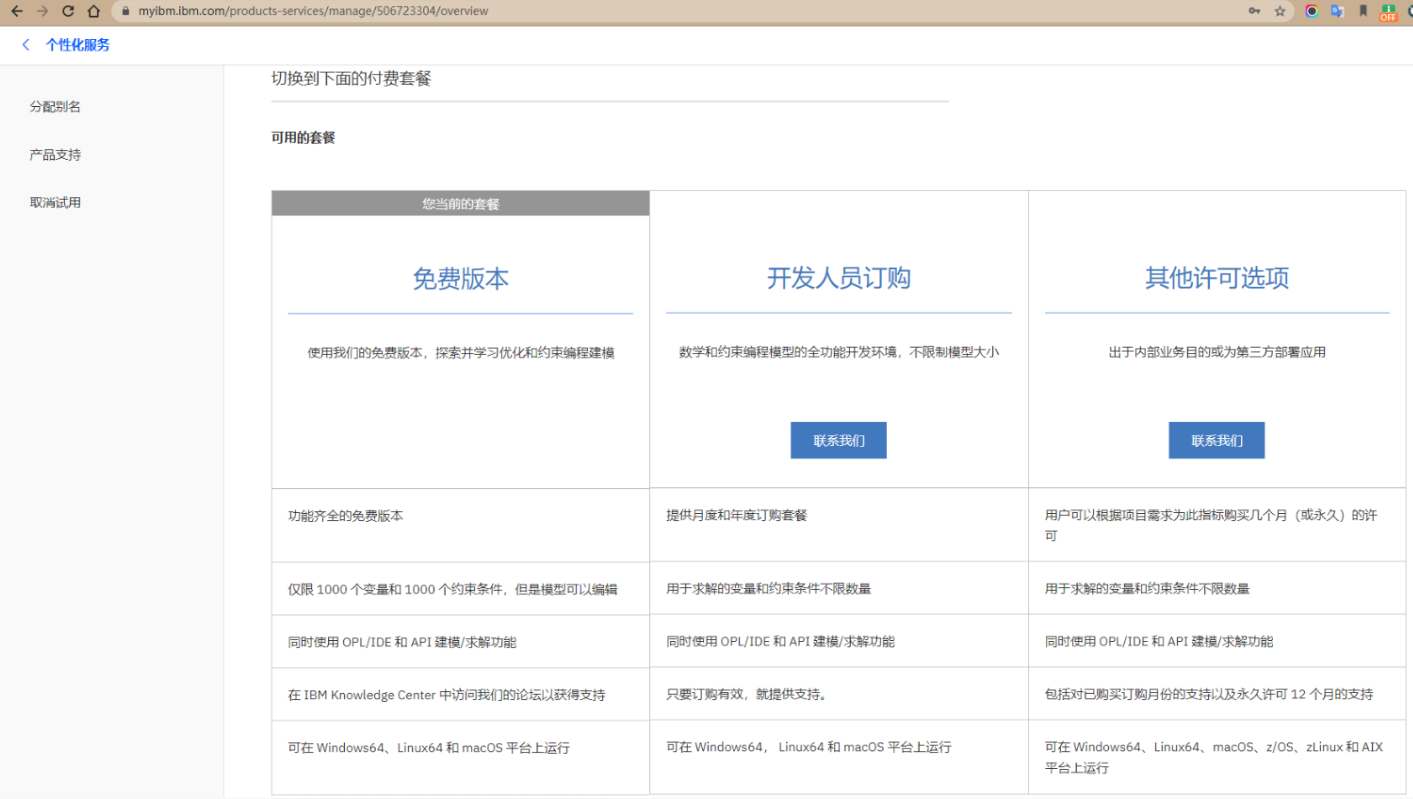
申請下載免費版本的時候,要先注冊一下填一些信息,然后會把下載地址發送到申請時的郵箱中,可以下載win、linux、macos版本。

這個安裝完之后是一個ide開發工具CPLEX_Studio,由于我是用idea開發的,所以還要配置如下的步驟:
CPLEX_Studio安裝完以后,安裝目錄下會有一個jar包,需要導入到我們的idea中,我是將jar包導入到我本地maven倉庫中,用pom引入的:
CPLEX_Studio中jar包的位置: D:\CPLEX_Studio_Community201\cplex\lib\cplex.jar
mvn install:install-file -Dfile=D:\CPLEX_Studio_Community201\cplex\lib\cplex.jar -DgroupId=cplex -DartifactId=cplex -Dversion=20.1.0.0.R1 -Dpackaging=jar
<dependency> <groupId>cplex</groupId> <artifactId>cplex</artifactId> <version>20.1.0.0.R1</version> </dependency>
然后在我們的啟動項目時還要加入java.library.path參數,指定CPLEX運行庫:
-Djava.library.path="D:\CPLEX_Studio_Community201\cplex\bin\x64_win64"
我在開發中是直接idea配置的:
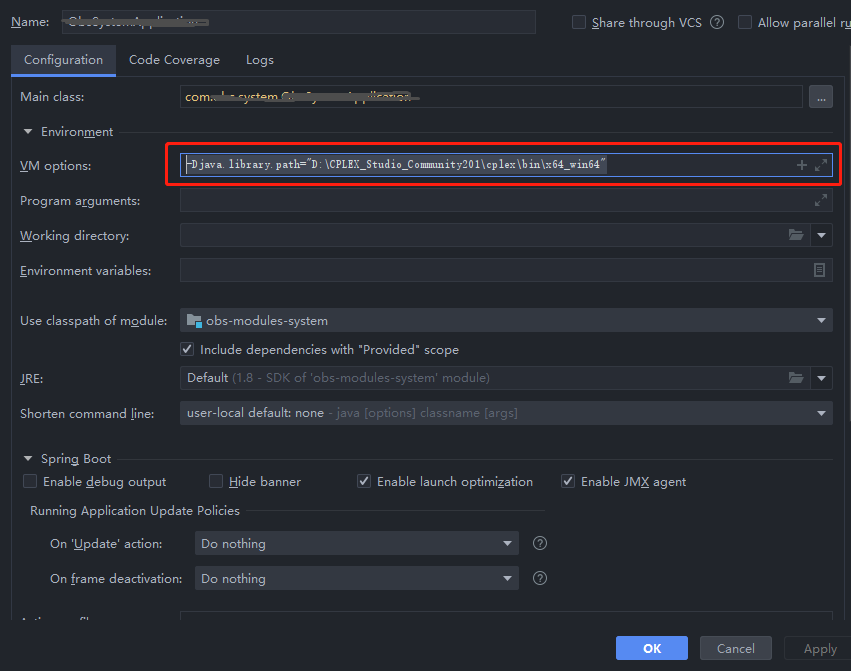
之后就可以愉快的使用了。
我項目中的不等式方程組是∑求和形式的,這里就手動打碼先假設決策變量的數量為 5 * 3 個,經過化簡后得到多元一次不等式組如下:
求解最大值 = AX + AY + AZ + BX + BY + BZ + CX + CY + CZ + DX + DY + DZ + EX + EY + EZ AX + AY + AZ <= 25400 BX + BY + BZ <= 18600 CX + CY + CZ <= 39800 DX + DY + DZ <= 53200 EX + EY + EZ <= 5900 AX + AY + AZ <= 10000 BX + BY + BZ <= 10000 CX + CY + CZ <= 10000 DX + DY + DZ <= 10000 EX + EY + EZ <= 10000 AX + BX + CX + DX + EX >= 15000 AY + BY + CY + DY + DY >= 5000 AZ + BZ + CZ + DZ + DZ >= 10000 (50.25-50)*AX + (49.86-50)*BX + (68.80-50)*CX + (49.79-50)*DX + (48.77-50)*EX >= 0 (50.25-60)*AY + (49.86-60)*BY + (68.80-60)*CY + (49.79-60)*DY + (48.77-60)*EY >= 0 (50.25-55)*AZ + (49.86-55)*BZ + (68.80-55)*CZ + (49.79-55)*DZ + (48.77-55)*DZ >= 0 (30.95*(1-2/100)-30)*AX + (31.52*(1-3/100)-30)*BX + (30.58*(1-1/100)-30)*CX + (30.17*(1-1/100)-30)*DX + (27.83*(1-1/100)-30)*EX >= 0 (30.95*(1-2/100)-30)*AY + (31.52*(1-3/100)-30)*BY + (30.58*(1-1/100)-30)*CY + (30.17*(1-1/100)-30)*DY + (27.83*(1-1/100)-30)*EY >= 0 (30.95*(1-2/100)-30)*AZ + (31.52*(1-3/100)-30)*BZ + (30.58*(1-1/100)-30)*CZ + (30.17*(1-1/100)-30)*DZ + (27.83*(1-1/100)-30)*EZ >= 0 (11.32*(1-2/100)-10)*AX + (12.83*(1-3/100)-10)*BX + (16.06*(1-1/100)-10)*CX + (5.68*(1-1/100)-10)*DX + (8.54*(1-1/100)-10)*EX >= 0 (11.32*(1-2/100)-10)*AY + (12.83*(1-3/100)-10)*BY + (16.06*(1-1/100)-10)*CY + (5.68*(1-1/100)-10)*DY + (8.54*(1-1/100)-10)*EY >= 0 (11.32*(1-2/100)-10)*AZ + (12.83*(1-3/100)-10)*BZ + (16.06*(1-1/100)-10)*CZ + (5.68*(1-1/100)-10)*DZ + (8.54*(1-1/100)-10)*EZ >= 0 (6*(1-2/100)-5)*AX + (4*(1-3/100)-5)*BX + (5*(1-1/100)-5)*CX + (2*(1-1/100)-5)*DX + (5*(1-1/100)-5)*EX <= 0 (6*(1-2/100)-5)*AY + (4*(1-3/100)-5)*BY + (5*(1-1/100)-5)*CY + (2*(1-1/100)-5)*DY + (5*(1-1/100)-5)*EY <= 0 (6*(1-2/100)-5)*AZ + (4*(1-3/100)-5)*BZ + (5*(1-1/100)-5)*CZ + (2*(1-1/100)-5)*DZ + (5*(1-1/100)-5)*EZ <= 0 非負約束: AX,AY,AZ,BX,BY,BZ,CX,CY,CZ,DX,DY,DZ,EX,EY,EZ >= 0
上面這些是根據我自己的項目得到的不等式組,可以根據自己的項目來做相應改動。
try {
// creat a model
IloCplex cplex = new IloCplex();
// 變量的取值范圍
double[] lb = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};
double[] ub = {10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000};
IloNumVar[] x = cplex.numVarArray(15, lb, ub);
// 求解目標
double[] objvals = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1};
cplex.addMaximize(cplex.scalProd(x, objvals));
// 不等式約束
cplex.addLe(cplex.scalProd(x, new double[]{1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 25400);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 18600);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0}), 39800);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0}), 53200);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1}), 5900);
cplex.addLe(cplex.scalProd(x, new double[]{1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 10000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 10000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0}), 10000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0}), 10000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1}), 10000);
cplex.addLe(cplex.scalProd(x, new double[]{1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 20000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0}), 20000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0}), 20000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0}), 20000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1}), 20000);
cplex.addLe(cplex.scalProd(x, new double[]{-1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0}), -15000);
cplex.addLe(cplex.scalProd(x, new double[]{0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0}), -5000);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1}), -10000);
cplex.addLe(cplex.scalProd(x, new double[]{50 - 50.25, 0, 0, 50 - 49.86, 0, 0, 50 - 68.80, 0, 0, 50 - 49.79, 0, 0, 50 - 48.77, 0, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 60 - 50.25, 0, 0, 60 - 49.86, 0, 0, 60 - 68.80, 0, 0, 60 - 49.79, 0, 0, 60 - 48.77, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 55 - 50.25, 0, 0, 55 - 49.86, 0, 0, 55 - 68.80, 0, 0, 55 - 49.79, 0, 0, 55 - 48.77}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{30 - 30.95 * 0.98, 0, 0, 30 - 31.52 * 0.97, 0, 0, 30 - 30.58 * 0.99, 0, 0, 30 - 30.17 * 0.99, 0, 0, 30 - 27.83 * 0.99, 0, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 30 - 30.95 * 0.98, 0, 0, 30 - 31.52 * 0.97, 0, 0, 30 - 30.58 * 0.99, 0, 0, 30 - 30.17 * 0.99, 0, 0, 30 - 27.83 * 0.99, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 30 - 30.95 * 0.98, 0, 0, 30 - 31.52 * 0.97, 0, 0, 30 - 30.58 * 0.99, 0, 0, 30 - 30.17 * 0.99, 0, 0, 30 - 27.83 * 0.99}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{10 - 11.32 * 0.98, 0, 0, 10 - 12.83 * 0.97, 0, 0, 10 - 16.06 * 0.99, 0, 0, 10 - 5.68 * 0.99, 0, 0, 10 - 8.54 * 0.99, 0, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 10 - 11.32 * 0.98, 0, 0, 10 - 12.83 * 0.97, 0, 0, 10 - 16.06 * 0.99, 0, 0, 10 - 5.68 * 0.99, 0, 0, 10 - 8.54 * 0.99, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 10 - 11.32 * 0.98, 0, 0, 10 - 12.83 * 0.97, 0, 0, 10 - 16.06 * 0.99, 0, 0, 10 - 5.68 * 0.99, 0, 0, 10 - 8.54 * 0.99}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{6 * 0.98 - 5, 0, 0, 4 * 0.97 - 5, 0, 0, 5 * 0.99 - 5, 0, 0, 2 * 0.99 - 5, 0, 0, 5 * 0.99 - 5, 0, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 6 * 0.98 - 5, 0, 0, 4 * 0.97 - 5, 0, 0, 5 * 0.99 - 5, 0, 0, 2 * 0.99 - 5, 0, 0, 5 * 0.99 - 5, 0}), 0);
cplex.addLe(cplex.scalProd(x, new double[]{0, 0, 6 * 0.98 - 5, 0, 0, 4 * 0.97 - 5, 0, 0, 5 * 0.99 - 5, 0, 0, 2 * 0.99 - 5, 0, 0, 5 * 0.99 - 5}), 0);
if (cplex.solve()) {
cplex.output().println("Solution status = " + cplex.getStatus());
cplex.output().println("Solution value = " + cplex.getObjValue());
double[] val = cplex.getValues(x);
for (int j = 0; j < val.length; j++) {
cplex.output().println("x" + (j+1) + " = " + val[j]);
}
}
cplex.end();
} catch (Exception e) {
System.err.println("Concert exception caught: " + e);
}
// Iteration log . . .
// Iteration: 1 Dual objective = 99025.641026
// Solution status = Optimal
// Solution value = 44280.112731282905
// x1 = 4022.4510446323093
// x2 = 0.0
// x3 = 5977.548955367691
// x4 = 10000.0
// x5 = 0.0
// x6 = 0.0
// x7 = 211.60418010554542
// x8 = 3814.5789532616586
// x9 = 5973.816866632794
// x10 = 0.0
// x11 = 801.3074331974203
// x12 = 9198.69256680258
// x13 = 2913.635241579134
// x14 = 384.1136135409201
// x15 = 982.3638761628501
// [INFO] ------------------------------------------------------------------------
// [INFO] BUILD SUCCESS
// [INFO] ------------------------------------------------------------------------
// [INFO] Total time: 2.757 s
// [INFO] Finished at: 2021-04-12T09:58:14+08:00
// [INFO] ------------------------------------------------------------------------感謝各位的閱讀,以上就是“java線性規劃問題舉例分析”的內容了,經過本文的學習后,相信大家對java線性規劃問題舉例分析這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。