您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要為大家展示了“如何使用matlab模擬退火算法單約束車間流水線調度”,內容簡而易懂,條理清晰,希望能夠幫助大家解決疑惑,下面讓小編帶領大家一起研究并學習一下“如何使用matlab模擬退火算法單約束車間流水線調度”這篇文章吧。
車間調度是指根據產品制造的合理需求分配加工車間順序,從而達到合理利用產品制造資源、提高企業經濟效益的目的。車間調度問題從數學上可以描述為有n個待加工的零件要在m臺機器上加工。問題需要滿足的條件包括每個零件的各道工序使用每臺機器不多于1次,每個零件都按照一定的順序進行加工。
傳統作業車間帶調度實例
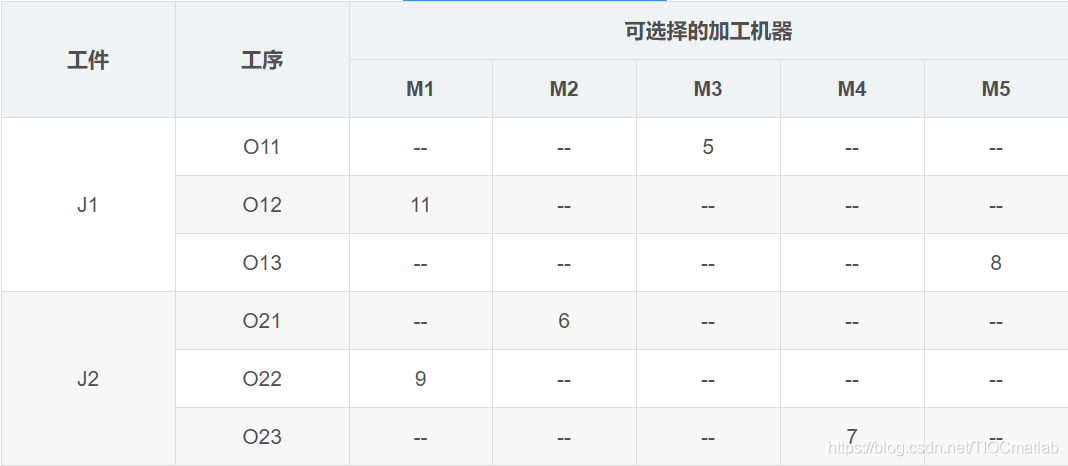
有若干工件,每個工件有若干工序,有多個加工機器,但是每道工序只能在一臺機器上加工。對應到上面表格中的實例就是,兩個工件,工件J1有三道工序,工序Q11只能在M3上加工,加工時間是5小時。
約束是對于一個工件來說,工序的相對順序不能變。O11->O12->O13。每時刻,每個工件只能在一臺機器上加工;每個機器上只能有一個工件。
調度的任務則是安排出工序的加工順序,加工順序確定了,因為每道工序只有一臺機器可用,加工的機器也就確定了。
調度的目的是總的完工時間最短(也可以是其他目標)。舉個例子,比如確定了O21->O22->O11->O23->O12->O13的加工順序之后,我們就可以根據加工機器的約束,計算出總的加工時間。
M2加工O21消耗6小時,工件J2當前加工時間6小時。
M1加工O22消耗9小時,工件J2當前加工時間6+9=15小時。
M3加工O11消耗5小時,工件J1當前加工時間5小時。
M4加工O23消耗7小時,工件J2加工時間15+7=22小時。
M1加工O12消耗11小時,但是要等M1加工完O22之后才開始加工O12,所以工件J1的當前加工時間為max(5,9)+11=20小時。
M5加工O13消耗8小時,工件J2加工時間20+8=28小時。
總的完工時間就是max(22,28)=28小時。
柔性作業車間帶調度實例(參考自高亮老師論文
《改進遺傳算法求解柔性作業車間調度問題》——機械工程學報)
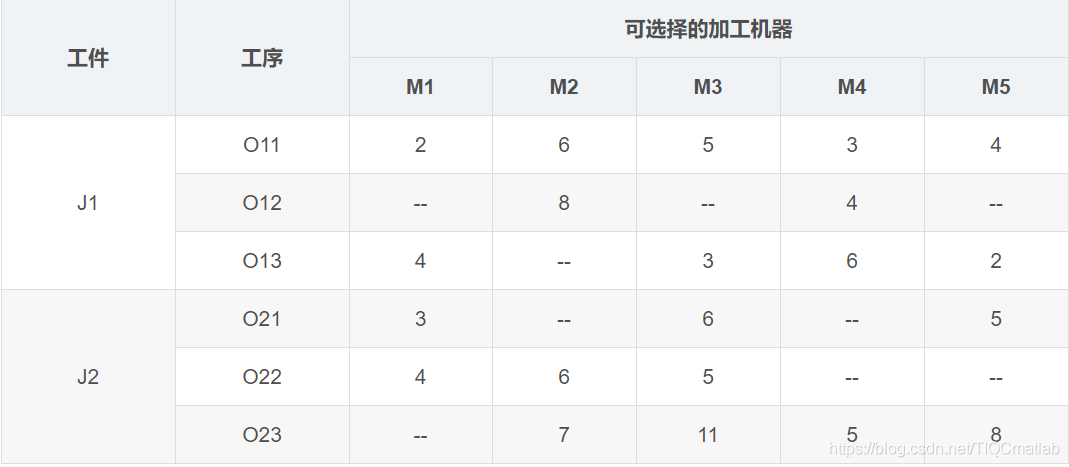
相比于傳統作業車間調度,柔性作業車間調度放寬了對加工機器的約束,更符合現實生產情況,每個工序可選加工機器變成了多個,可以由多個加工機器中的一個加工。比如上表中的實例,J1的O12工序可以選擇M2和M4加工,加工時間分別是8小時和4小時,但是并不一定選擇M4加工,最后得出來的總的完工時間就更短,所以,需要調度算法求解優化。
相比于傳統作業車間,柔性車間作業調度的調度任務不僅要確定工序的加工順序,而且需要確定每道工序的機器分配。比如,確定了O21->O22->O11->O23->O12->O13的加工順序,我們并不能相應工序的加工機器,所以還應該確定對應的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的機器組合。調度的目的還是總的完工時間最短(也可以是其他目標,比如機器最大負荷最短、總的機器負荷最短)


5 模擬退火算法的參數
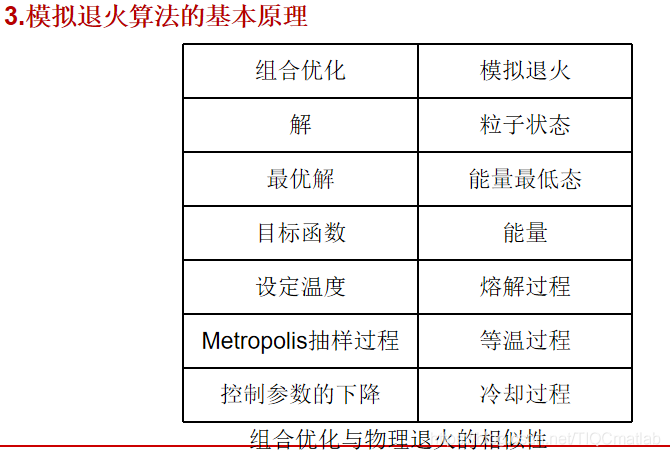
模擬退火是一種優化算法,它本身是不能獨立存在的,需要有一個應用場合,其中溫度就是模擬退火需要優化的參數,如果它應用到了聚類分析中,那么就是說聚類分析中有某個或者某幾個參數需要優化,而這個參數,或者參數集就是溫度所代表的。它可以是某項指標,某項關聯度,某個距離等等。
clc;
clear;
close all;
%% Problem Definition
model=CreateModel(); % Create Model of the Problem
CostFunction=@(q) MyCost(q,model); % Cost Function
nVar=model.nVar; % Number of Decision Variables
VarSize=[1 nVar]; % Size of Decision Variables Matrix
%% SA Parameters
MaxIt=100; % Maximum Number of Iterations
MaxIt2=25; % Maximum Number of Inner Iterations
T0=10; % Initial Temperature
alpha=0.97; % Temperature Damping Rate
%% Initialization
% Create Initial Solution
x.Position=CreateRandomSolution(model);
[x.Cost, x.Sol]=CostFunction(x.Position);
% Update Best Solution Ever Found
BestSol=x;
% Array to Hold Best Cost Values
BestCost=zeros(MaxIt,1);
% Set Initial Temperature
T=T0;
%% SA Main Loop
for it=1:MaxIt
for it2=1:MaxIt2
% Create Neighbor
xnew.Position=CreateNeighbor(x.Position);
[xnew.Cost, xnew.Sol]=CostFunction(xnew.Position);
if xnew.Cost<=x.Cost
% xnew is better, so it is accepted
x=xnew;
else
% xnew is not better, so it is accepted conditionally
delta=xnew.Cost-x.Cost;
p=exp(-delta/T);
if rand<=p
x=xnew;
end
end
% Update Best Solution
if x.Cost<=BestSol.Cost
BestSol=x;
end
end
% Store Best Cost
BestCost(it)=BestSol.Cost;
% Display Iteration Information
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
% Reduce Temperature
T=alpha*T;
% Plot Solution
figure(1);
PlotSolution(BestSol.Sol,model);
pause(0.01);
end
%% Results
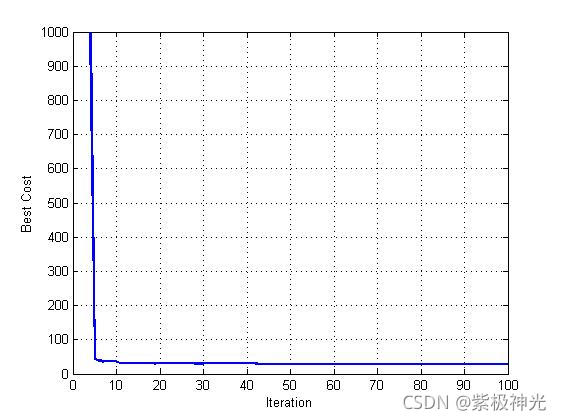
figure;
plot(BestCost,'LineWidth',2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;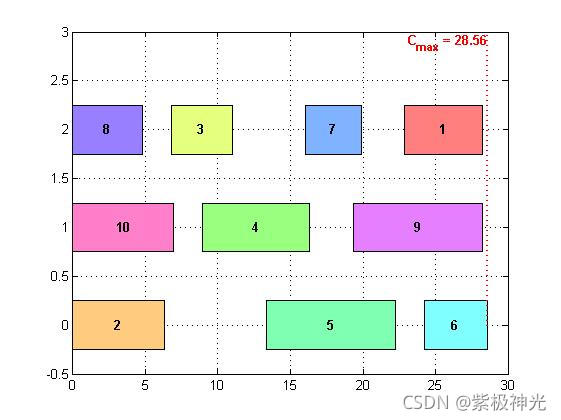
以上是“如何使用matlab模擬退火算法單約束車間流水線調度”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。