您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了C++中二分法是什么,具有一定借鑒價值,感興趣的朋友可以參考下,希望大家閱讀完這篇文章之后大有收獲,下面讓小編帶著大家一起了解一下。
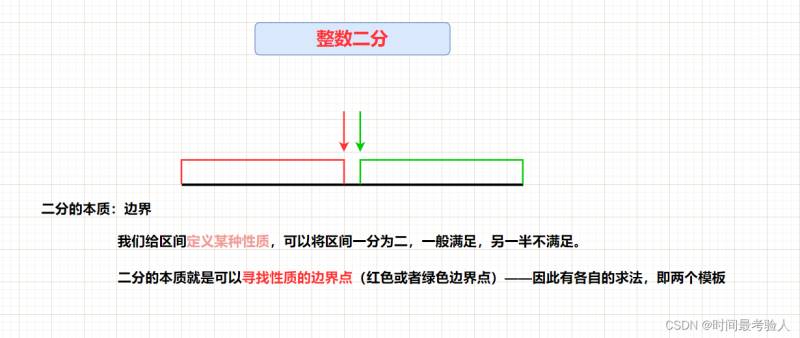
單調性與二分的關系:有單調性一定可以二分,用二分不一定是單調性。二分的本質不是單調性而是邊界點(找符合條件的最小的數或者最大的數)整數二分是求紅色范圍的右端點 或者 綠色范圍的左端點
bool check(int x) {/* ... */} // 檢查x是否滿足某種性質
// 區間[l, r]被劃分成[l, mid]和[mid + 1, r]時使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判斷mid是否滿足性質
else l = mid + 1;
}
return l;
}
// 區間[l, r]被劃分成[l, mid - 1]和[mid, r]時使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}【模板1】
1、求紅色邊界點
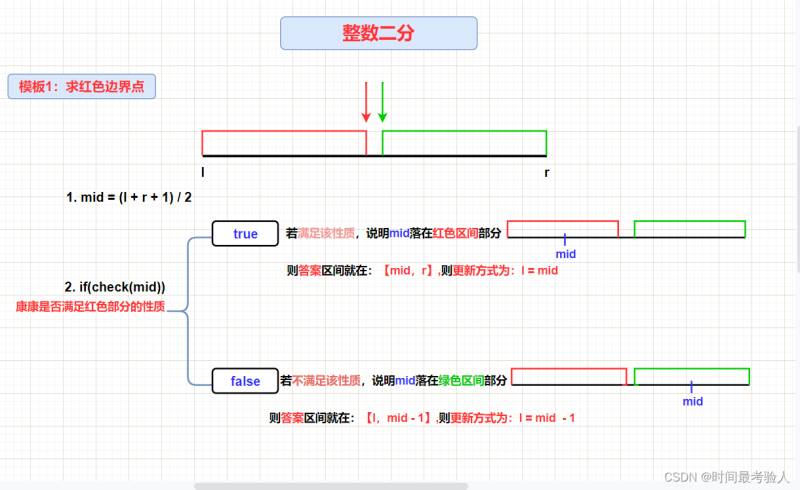
注: + 1原因:
/ 是向下取整,當l與r只相差1的時候,即 l = r - 1,最終的結果mid = l(即結果不變還是l),補上1之后 mid = r,再次循環之后l = r 即[r , r],最終結束循環。如果不補1將會出現死循環。
【模板2】
求綠色邊界點
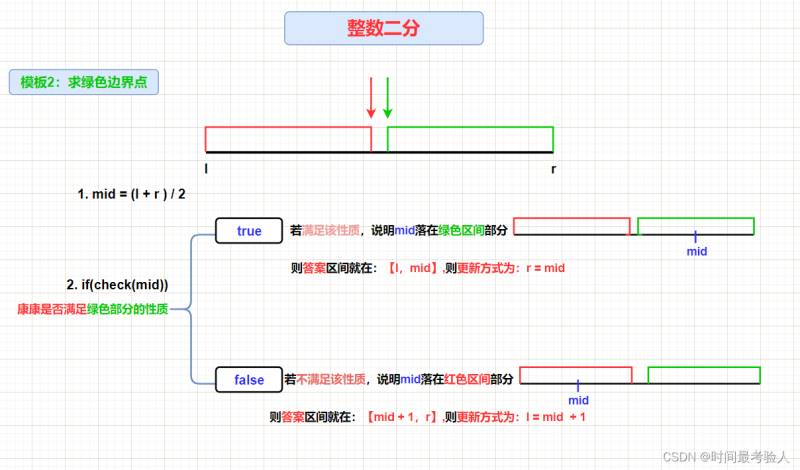
每次先劃分區間,寫一個mid,后面再考慮是否補上加1操作然后想一個check()函數,康康是否滿足性質,根據check()函數的值取判斷怎么劃分(mid在哪一邊),到底是是l = mid,還是r = mid,第一種補上1即可。(關鍵是找性質,判斷是否滿足性質然后判斷mid在左邊還是右邊)
(1).數的范圍
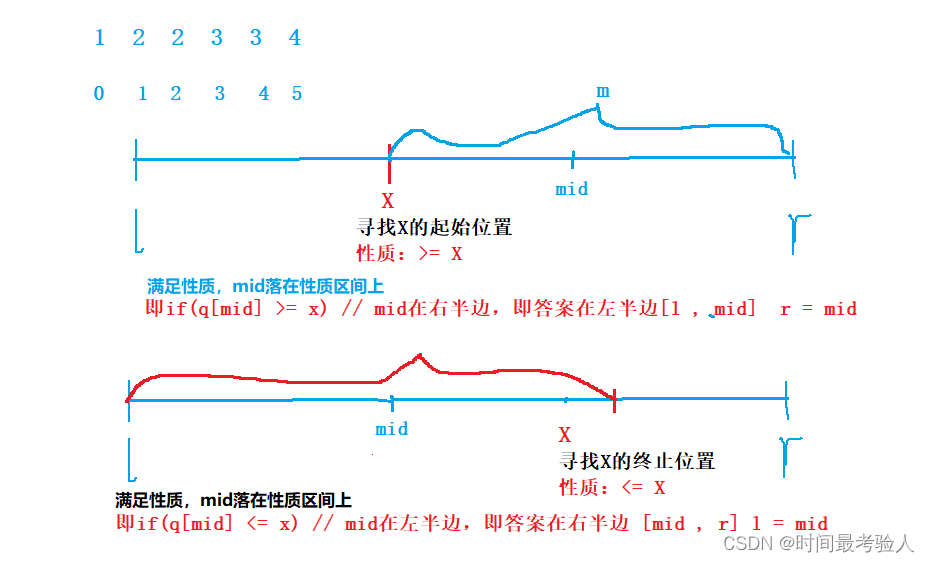
給定一個按照升序排列的長度為 nn 的整數數組,以及 qq 個查詢。
對于每個查詢,返回一個元素 kk 的起始位置和終止位置(位置從 00 開始計數)。
如果數組中不存在該元素,則返回
-1 -1。輸入格式
第一行包含整數 n 和 q,表示數組長度和詢問個數。
第二行包含 nn 個整數(均在 1∼10000 范圍內),表示完整數組。
接下來 q行,每行包含一個整數 k,表示一個詢問元素。
輸出格式
共 q 行,每行包含兩個整數,表示所求元素的起始位置和終止位置。
如果數組中不存在該元素,則返回
-1 -1。數據范圍
1≤n≤100000
1≤q≤10000
1≤k≤10000輸入樣例:
6 31 2 2 3 3 4345輸出樣例:
3 45 5-1 -1
思路:
【參考代碼】
#include<iostream>
using namespace std;
const int N = 100000+10;
int q[N];
int main()
{
int n, m;
cin>> n >> m;
for(int i = 0; i < n; i++) cin>>q[i];
while(m--)
{
int x;
cin>> x;
// 尋找起始位置
int l = 0, r = n - 1;
while(l < r)
{
int mid =(l + r)/2;
if(q[mid] >= x) r = mid;
else l = mid + 1;
}
if(q[l] != x) cout<<"-1 -1"<<endl;
else{
cout<<l<<" ";
// 尋找終點位置
int l = 0, r = n - 1;
while(l<r)
{
int mid = (l + r + 1)/2;
if(q[mid] <= x) l = mid;
else r = mid - 1;
}
cout<< l << endl;
}
}
return 0;
}(2).0到n-1中缺失的數字
(二分) O(logn)
這道題目給定的是遞增數組,假設數組中第一個缺失的數是 x,那么數組中的數如下所示;

從中可以看出,數組左邊藍色部分都滿足nums[i] == i,數組右邊橙色部分都不滿足nums[i] == i,因此我們可以二分出分界點 x 的值。
另外要注意特殊情況:當所有數都滿足nums[i] == i時,表示缺失的是 n。
時間復雜度分析
二分中的迭代只會執行 O(logn) 次,因此時間復雜度是O(logn)。

class Solution {
public:
int getMissingNumber(vector<int>& nums) {
if(nums.size() == 0) return 0;
int l = 0, r = nums.size() - 1;
while(l < r)
{
int mid = (l + r)/2;
if(nums[mid] != mid) r = mid; //在紅色半邊(滿足條件)
else l = mid + 1;
}
//缺的是n這個數
if(nums[r] == r) r++;
return r;
}
};浮點數二分算法模板 —— 模板題 AcWing 790. 數的三次方根
bool check(double x) {/* ... */} // 檢查x是否滿足某種性質(包含了計算和條件)
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取決于題目對精度的要求(一般比題目要求的大2)
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}注:與整數二分的最大區別是,else那里的條件l = mid不進行+1或者-1,浮點數沒有整除(/ 下取整)這種問題,不需要處理邊界。
(1).數的三次方跟
給定一個浮點數 n,求它的三次方根。
輸入格式
共一行,包含一個浮點數 n。
輸出格式
共一行,包含一個浮點數,表示問題的解。
注意,結果保留 6 位小數。
數據范圍
−10000≤n≤10000
輸入樣例:
1000.00輸出樣例:
10.000000
#include<iostream>
using namespace std;
int main()
{
double n;
cin>>n;
double l = -10000, r = 10000;
// eps 表示精度,取決于題目對精度的要求(保險1e-8)
const double eps = 1e-8;
while(r - l > eps)
{
double mid = (l + r) / 2;
if(mid * mid * mid >= n) r = mid;
else l = mid;
}
printf("%.6lf\n", l);
return 0;
}(2).一元三次方程求解

提示:記方程f(x)=0,若存在2個數x1和x2,且f(x1)*f(x2)<0,則在(x1,x2)之間一定有一個根。
#include<iostream>
#include<cstdio>
using namespace std;
double a, b, c, d;// 全局變量方便在cal中使用
const double eps = 1e-6;// 定義精度
//計算一元三次方程
double cal(double x)
{
return a*x*x*x + b*x*x + c*x + d;
}
int main()
{
cin>>a>>b>>c>>d;
//枚舉根
for(int i = -100; i <= 100; i++)
{
//根與根之差的絕對值 ≥1
double l = double(i), r = double(i + 1);// 細節:要將l,r轉為double
if(cal(l) == 0) printf("%.2lf ", l); //若f(x) = 0,根即為x
//f(x1)×f(x2) < 0 根在(x1,x2)之間—— 浮點二分
else if(cal(l) * cal(r) < 0)
{
while(r - l > eps)
{
//x1 < x,f(x1)×f(x2)<0,則在(x1, x2)之間一定有一個根
double mid = (l + r)/2;
// check()條件
if(cal(l) * cal(mid) <= 0) r = mid;
else l = mid;
}
printf("%.2lf ", l);
}
}
}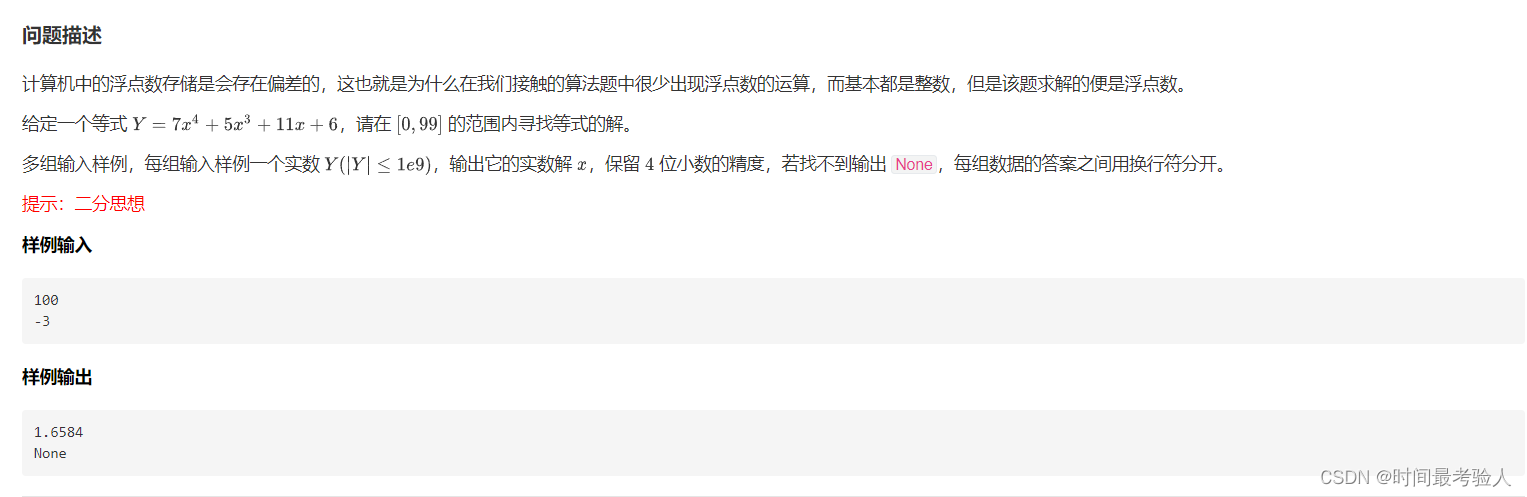
【參考代碼】
#include <bits/stdc++.h>
using namespace std;
double check(double x)
{
return 7*x*x*x*x + 5*x*x*x + 11*x + 6;
}
double erfen(double Y)
{
double l=0.0, r=99.0, mid;
while(r - l > 1e-6){
mid = (l + r)/2;
if(check(mid) > Y) r = mid;
else l = mid;
}
return mid;
}
int main()
{
double Y;
while(~scanf("%lf", &Y)){
if(Y < 6 || Y > 677269824)
puts("None");
else
printf("%.4f\n", erfen(Y));
}
return 0;
}感謝你能夠認真閱讀完這篇文章,希望小編分享的“C++中二分法是什么”這篇文章對大家有幫助,同時也希望大家多多支持億速云,關注億速云行業資訊頻道,更多相關知識等著你來學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。