您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關C++如何實現二分法求方程,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
二分法是一種求解方程近似根的方法。對于一個函數 f(x)f(x),使用二分法求 f(x)f(x) 近似解的時候,我們先設定一個迭代區間(在這個題目上,我們之后給出了的兩個初值決定的區間 [-20,20]),區間兩端自變量 x 的值對應的 f(x) 值是異號的,之后我們會計算出兩端 x 的中點位置 x' 所對應的 f(x') ,然后更新我們的迭代區間,確保對應的迭代區間的兩端 x 的值對應的 f(x) 值還會是異號的。
重復這個過程直到我們某一次中點值 x' 對應的 f(x') < f(x′)<? (題目中可以直接用EPSILON)就可以將這個 x′ 作為近似解返回給 main 函數了。
例如:
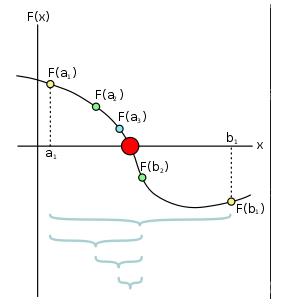
上面所示的一個迭代過程的第一次的迭代區間是 [a1,b1],取中點 b2,然后第二次的迭代區間是 [a1,b2],再取中點 a2,然后第三次的迭代區間是 [a2,b2],然后取 a3,然后第四次的迭代區間是[a3,b2],再取紅色中點 c,我們得到發現 f(c) 的值已經小于?,輸出c 作為近似解。
在這里,我們將用它實現對形如 px+q=0 的一元一次方程的求解。
在這里,你完成的程序將被輸入兩個正整數 p 和 q(你可以認為測評機給出的 0<∣p∣≤1000 且0<∣q∣≤1000),程序需要用二分法求出 px+q=0 的近似解。
測評機會反復運行你的程序。每次程序運行時,輸入為一行,包括一組被空格分隔開的符合描述的正整數 p 和 q。你可以認為輸入數據構成的方程 px+q=0 都是有解且解在[?20,20] 的區間內。
輸出為一行,包括一個數字。為方程 px+q=0 的近似解。請使用四舍五入的方式保留小數點后 4 位小數。
樣例輸入1
55 9
樣例輸出1
-0.1636
樣例輸入2
-22 4
樣例輸出2
0.1818
代碼:
#include <cstdio>
#include <cmath>
#define EPSILON 1e-7
double bisection(int p, int q, double (*func)(int, int, double));
double f(int p, int q, double x);
int main() {
int p;
int q;
scanf("%d %d", &p, &q);
printf("%.4lf\n", bisection(p, q, f));
return 0;
}
double bisection(int p, int q, double (*func)(int, int, double)) {
double x1 = -20;
double x2 = 20;
double x = 0;
while(fabs((*func)(p,q,x))>EPSILON)
{
x = (x1+x2)/2.0;
double fx1 = (*func)(p,q,x1);
double fx = (*func)(p,q,x);
if(fx*fx1>0)
{x1 = x;}
else
{x2 = x;}
}
return x;
}
double f(int p, int q, double x) {
return p * x + q;
}關于“C++如何實現二分法求方程”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,使各位可以學到更多知識,如果覺得文章不錯,請把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。