命題作文：Dimension Tree區間查找與IP數據包分類

這個題目有點大，而且我要嚴格控制字數，不能像《命題作文：在一棵IPv4地址樹中徹底理解IP路由表的各種查找過程》那樣扯得那么開了。事實上，這篇作文是上 一篇作文中關于區間查找小節的擴展。

1.IP數據包分類

根據IP數據包協議頭的若干字段，也叫匹配域，將數據包劃分到某個類別，這就是IP數據包分類的核心。
       事實上，IP路由查找的過程就是IP數據包分類的一個特例，一個極其簡單的特例，此時的匹配域就是目標IP地址，而類別就是路由項或者說更簡單一點，下一 跳。此時考慮一下源地址Policy routing，隨即又增加了一個匹配域，即源IP地址，這時整個過程應該怎么做呢？本文關注一種多維區間匹配方案，不談其它的比如HASH匹配，也不談 硬件算法。

2.區間查找

我希望我寫的《HiPAC高性能規則匹配算法之查找過程》以及《玩轉高性能超猛防火墻nf-HiPAC》可以帶來些幫助，其實，IP數據包分類的過程可以看成是多個匹配域的區間查找的結果的合并。
       在HiPAC一般算法中，雖然在執行效率上講是非常好的，但是卻可能浪費大量的內存。可能需要采用Grid of Tries數據結構的優化方式對其存儲空間進行優化，去除冗余數據。
       雖然我要說的關于IP數據包分類的核心算法到此應該就結束了，但是數據包分類背后的理論，才剛剛開始。后面我會用一個實例來做盡可能明晰的圖解，而不是用一個統一的數學推導來說明問題，目的在于提供一個感性的畫面。

3.問題的提出

往往只知道如何在多維連續區間集合里讓一個IP數據包是遠遠不夠的，其實不懂這些也沒關系。如果確實懂這個，那么就要知其然亦知其所以然。
       現在，我假設通過上面提到的兩篇關于nf-HiPAC的文章，你已經知道了多維區間匹配的過程，那么我們可以脫離具體場景了，將其抽象成一個一般問題，先 看一下抽象后的示意圖，在這個圖中，我忽略了區間的大小，忽略了Rule的排列問題(最終我將會回到這個問題)：

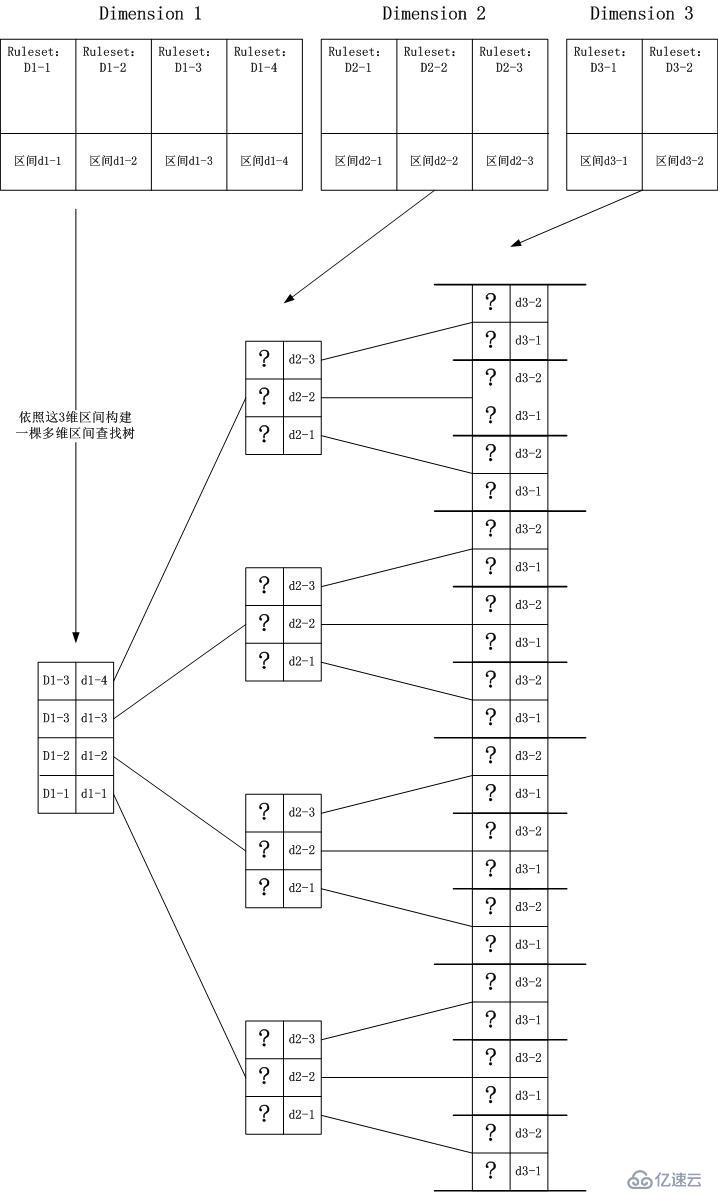
在這個圖中，我們看到了很多的“?”號，意思是說，我們此時并不知道和該區間相關的Ruleset是什么？這是為什么呢？
       我們來看第二層，也就是Dimension 2的那一層，該層中有4個節點，對應Dimension 1分裂出來的4個區間，如果想讓匹配繼續下去，即繼續匹配Dimension 3那一層的節點，對應的Ruleset中必須要有交集才可以，因此我們得到了下面這個更加清晰的圖示，雖然，它有點亂。。。。在寫這個文章時，我不知怎么 想起了哈爾濱，想哭...：

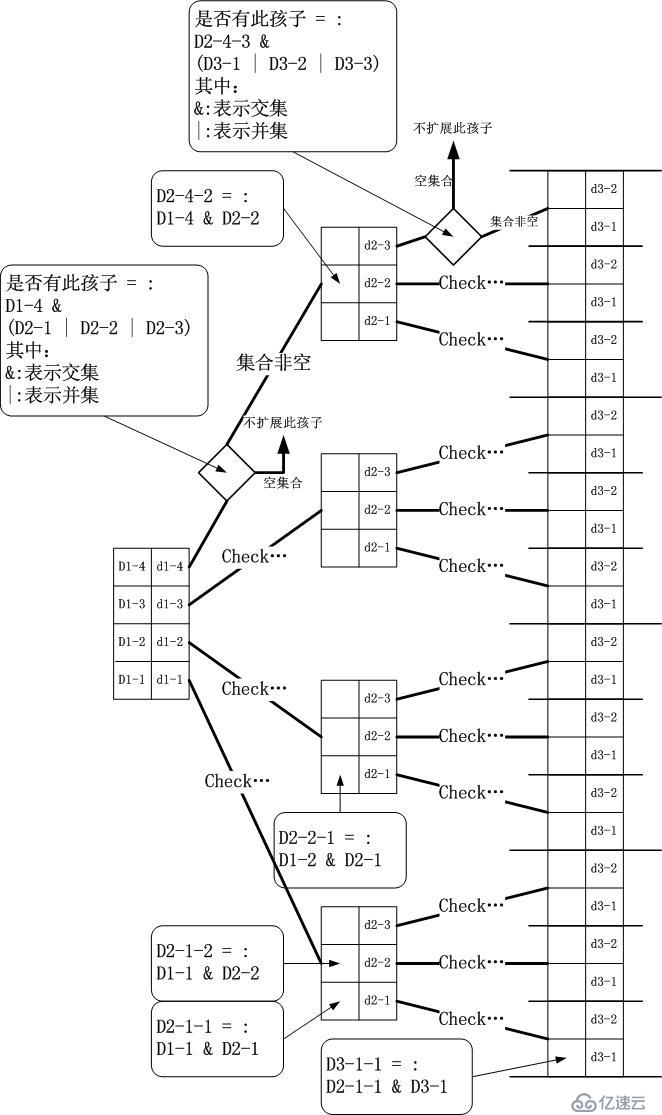
我們依照這個圖，發現了下面重要的三個關鍵點：

1).關鍵操作：Ruleset需要取交集

當 前區間的Ruleset與下一個維度的各個區間的Ruleset并集取交集，該結果集合不為空時才會擴展該分支成一個孩子節點。我加入了一些與場景相關的 約束，比如每一個區間起碼要有一個Default Rule，因此所有的取交集的結果均不會為空，所以上面的這句話應該是，如果結果集合的元素個數為1，且該元素為Default Rule的話，則該當前區間對應的下一個匹配維度孩子擴展為葉子節點。這意味著，下下一個維度將不會再擴展該子樹，也就是說匹配沒有必要繼續下去了，直接 取Default Rule即可。

2).關鍵權衡：快速成功與快速失敗

如關鍵操作所示，只要匹配會繼續進行下去，即相關的當前 區間剩余的Ruleset中Rule數量不為1或者為1但是不是Default Rule，那么我們就不能確定最終結果，因此，這意味著快速成功是不可能的。但是我們卻可以很快確定什么情況下會失敗，即當前區間的Ruleset中只剩 下了1個Default Rule。這就是快速失敗。

3).關鍵問題：這棵樹如何布局

通過上面的圖示可以看出，由于 Ruleset是取交集，Dimension 1/2/3誰在前誰在后其實最終并不影響結果，但是這個排序的不同卻可以影響空間的占用，從上圖可以看出，只要Ruleset有交集，就要在下層創建一個 孩子節點，其實就是創建一個區間查找樹，而我們在快速失敗中知道，所有的子樹可能由于Ruleset布局的不同而導致其高度并不相同。問題是，我們如何來 排列維度的查找順序？

4.困難的所在

不要指望在上面的那棵樹上作什么平衡操作，因為影響其子樹高度以及寬度的因素是相互關聯的，它們是Rule的數量，每一個維度的區間數量，Ruleset的內部布局等。這棵樹的任意“旋轉”將會導致其稱為一團亂麻，它不是三角架。
       由于根本就沒有好的辦法去計算如何最優化排列這些維度匹配順序，倒不如按照統計的意義，尋找一種“讓這棵樹”更加平衡的方式。

5.從M叉樹到2叉樹

到 此為止，我們一直覺得所謂的多維區間匹配就是一個M叉樹，其中M是每層由該層，即該維度所被劃分的區間數量。通過以上的分析，我們發現在一個如此胖的且每 個分支的高度還不確定的樹中尋找一種最佳的構建方式是一件困難的事情，因為變量太多了，Ruleset中Rule的數量是一個變參，區間數量也是一個變 參，各個維度的每一個區間的Ruleset都要取并集，這涉及到一個笛卡爾積的問題。這里面涉及太多的數學計算，又沒有一個簡單的公式。
       難道多維區間匹配樹一開始就必須如此構造成M叉樹嗎？
       在繼續之前，我來用一種更加直觀的方式展示上述的多維匹配問題，然后從0開始，直到我們遇到KD樹為止，剩下的內容，數據結構，算法相關的書上就都有了。

5.1.多維匹配立方體

幸虧我以三維域匹配為例，要不然我真不知道四維立方體怎么畫出來。
       我把上面的三維域匹配問題以一個立方體來描述：

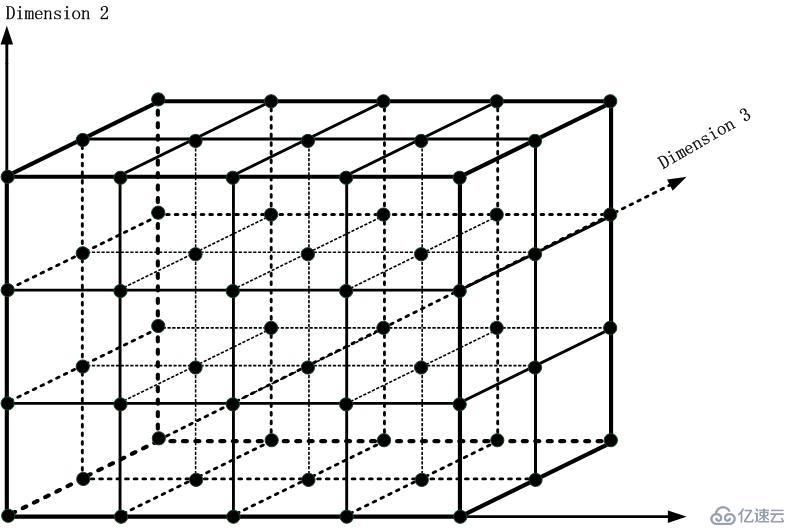
注 意到，每一個黑色的點沿著坐標軸連接成的線段進而由這些線段形成的面將這個立方體分割成了4*3*2個子立方體，我們的問題就是，最終匹配完成后，我們會 落入一個子立方體中，而這個子立方體里面當前的Ruleset就是結果集，我們取優先級最大的，就是最終結果，值得注意的是，這些子立方體中的 Ruleset是在構造這個立方體的時候放進去的，和那篇講路由查找的命題作文一樣，我并不考慮相對稀有的數據結構構造事件的時間復雜度。因此，我將 Ruleset示意圖放入子立方體，如下圖所示：

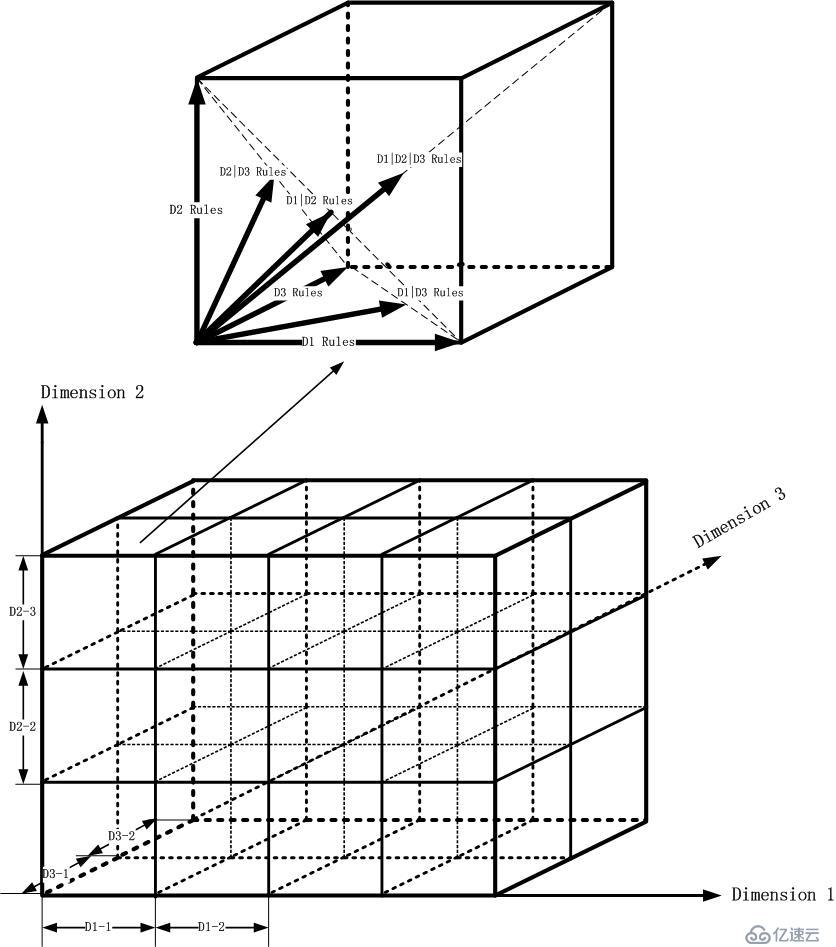
那么現在問題來了。我要怎么切割這個立方體，然后最后得到那個期望的子立方體呢？第一刀怎么切？沿著D1軸？D2軸？D3軸？如果確定了D1軸，那么第二刀呢？繼續D1軸？還是換一個方向切？...

5.2.切割方式

這不禁讓人想到切西瓜，但是事實上卻完全不同，這個和你用一大塊木頭塊取中心的小塊比較類似。你有兩種方式，先把它削成片，再把它削成棍，最后把棍剁成小塊；還有一種方式比較類似機床×××那般，始終不斷變換方向切割。對于多維匹配問題，我們面臨了同樣的選擇。

5.2.1.逐維度深度優先

這種方式類似片-棍-塊的方式，如下圖所示：

5.2.2.逐維度廣度優先

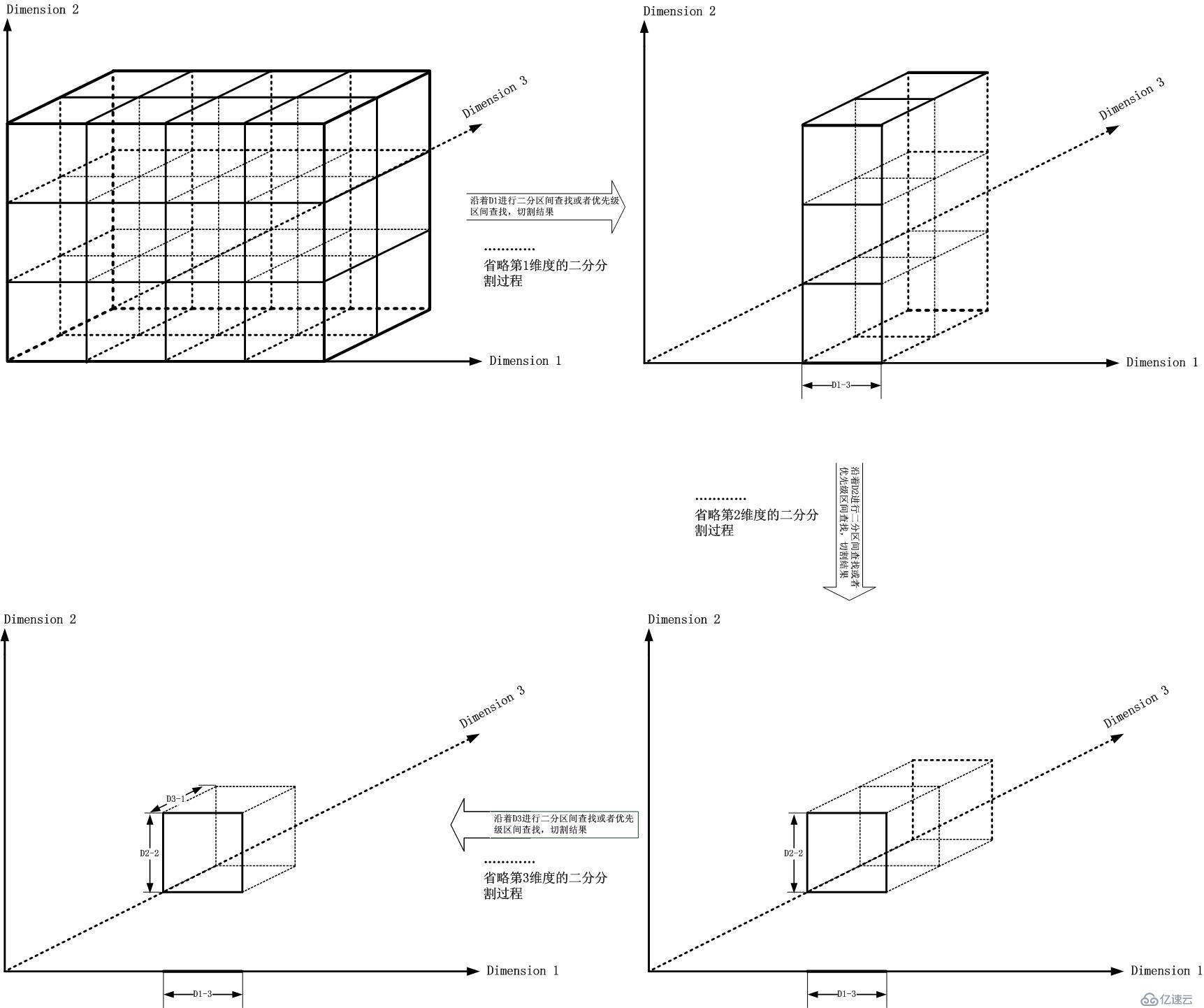
這個比較類似機器加工的方式，如下圖所示：

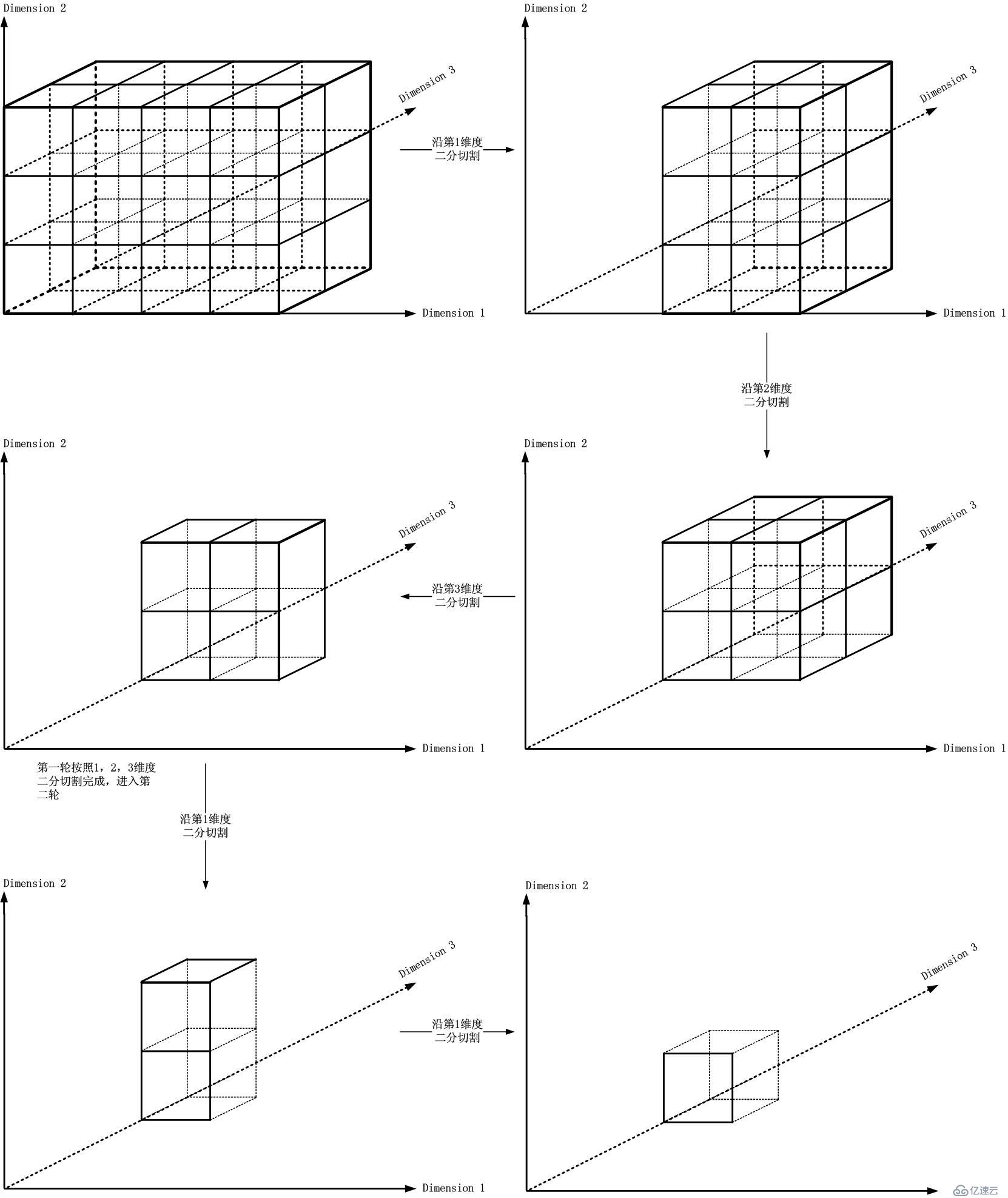
那么，是時候給出數據結構了。我在講路由查找的作文中的區間查找小節給出了區間二叉查找樹的結構以及構造方式，本文中對此前提作了基本假設。

5.3.深度優先查找樹

深度優先的查找樹結構如下：

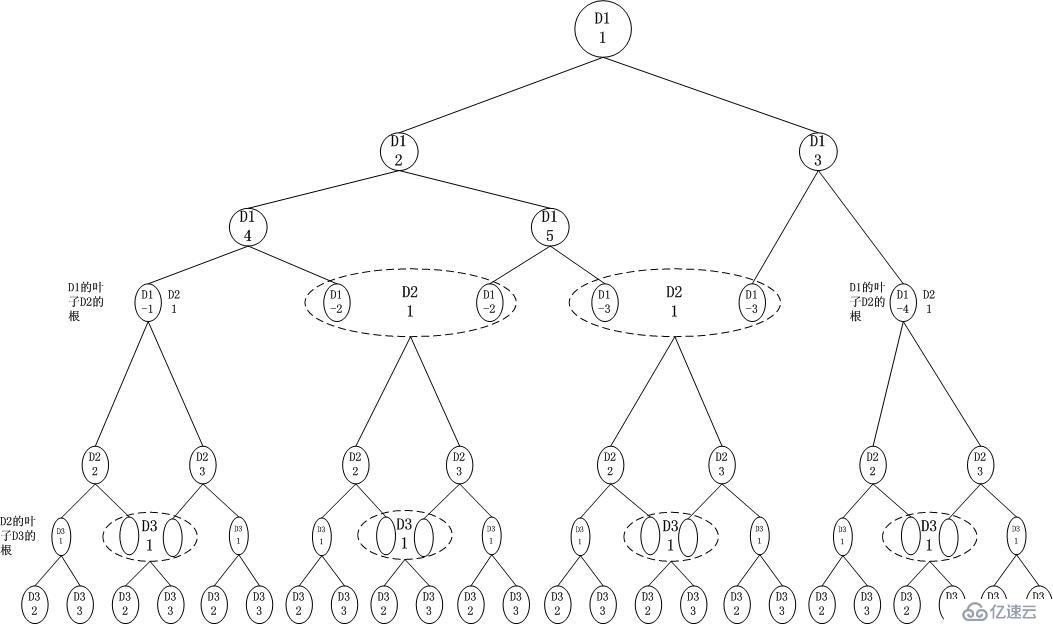
可見，這是一種直接的方式，特別適合精確匹配。以下我提到Dimension Tree或者Dimtree的時候，指的就是這棵樹。

5.4.廣度優先查找樹

廣度優先的查找樹結構如下：

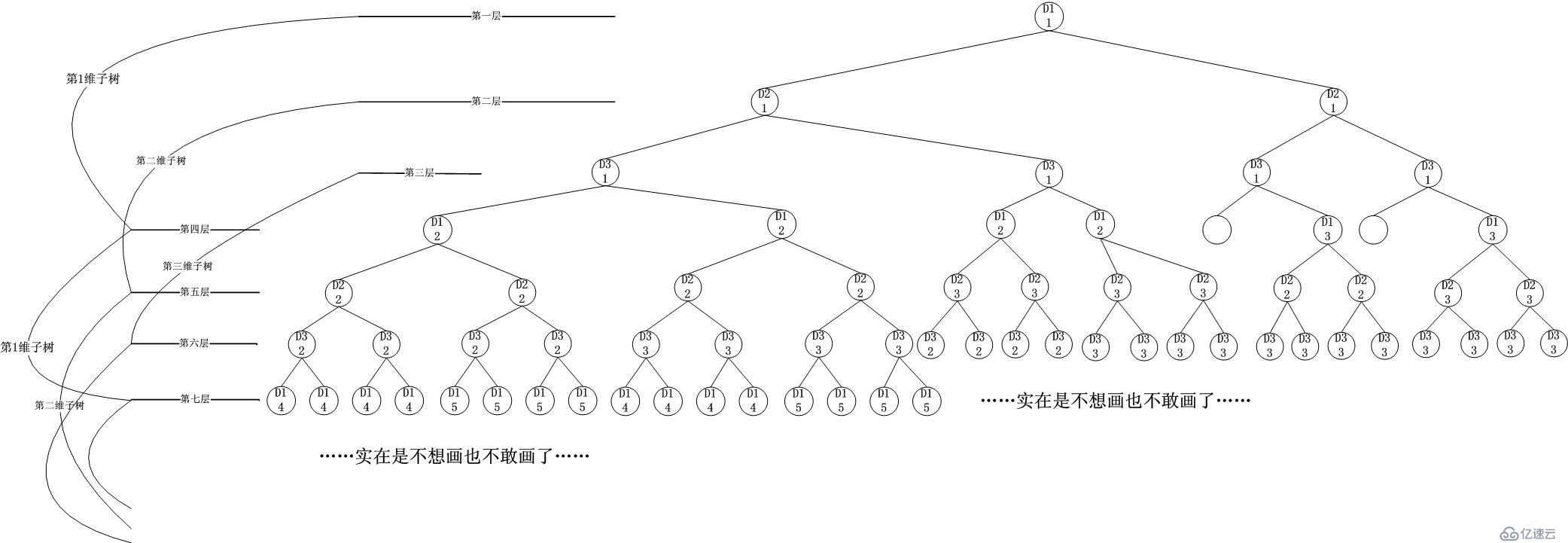
可 見，這是一種碰運氣的方式，在各個維度上逐步(以盡可能細的粒度，小心翼翼地)接近最終要落到的子立方體空間。當然這種方式其實就是Dimension Tree的逐層旋轉后展開的結果，最終也可以得到答案，碰到某個維度的葉子節點后，將其中的Ruleset壓入一個棧中，最終在這棵樹游歷結束后，將棧里 面的Ruleset取出后求交集，然后取最佳的即可。當然，也可以用快速失敗來剪掉枝干，比如到達了一個只包含Default Rule的葉子節點。但是，第一次發現葉子節點的時刻要等多久呢？如果第一個維度的查找樹有3層，第二維度有2層，第三維度有2層，那么廣度優先樹的層則 為：第一維度-第二維度-第三維度-第一維度-第二維度(首次碰到葉子)-第三維度(葉子節點)-第一維度....不管怎么說，即便從第二維度開始切割， 也不可能在第二層碰到葉子...這就說明，即便是快速失敗的檢測，也要比深度優先延后。

5.5.比較

對于數據包精確匹配分類來 講，深度優先的方式好于廣度優先的方式，這不僅僅是在說如果沒有精確區間匹配，那么再接近的匹配也不算(比如精確匹配192.168.1.18，那么 192.168.1.19顯然是不符合要求的，雖然它很接近)，還包括這種方式可以最大限度的利用系統Cache。
       注意，不要認為數據包的掩碼匹配就不是精確匹配，本文是嚴格基于區間來匹配的，掩碼將一個域劃分成了多個精確的區間，而最終的目的是定位一個數據包的某個域精確落到了哪個區間中，注意，這是一種精確匹配。
       KD樹，即k-dimension樹就采用了上述逐維度廣度優先的匹配方式。然而它的維度排序思想可以被借鑒，從而用于深度優先匹配，最終目標是構建一棵“若不匹配則快速失敗”的樹！

注解：k-dimension樹

看起來，這像極了一棵B-樹，但它不是！
KD樹的資料網上實在太多。我要說的是它的遞歸構建中是如何使用方差的。現在讓我們回答第一刀從哪里切割的問題。
       我將區間長度作為基準，那么每個維度均可以計算出一個區間長度的方差數值，即：



取這個值最大的維度為第一維度，然后使用樸素的二分構建，取該維度區間全集中最接近中點的那個點作為根，開始遞歸構建二叉樹。每一層都要計算該子域的方差，從而根據這個最大方差原則選出子樹的二分根。通過上面的廣度優先匹配可以看出，那個圖應該就是一棵樸素的KD樹。
       采用最小方差的思想的目的是，讓這棵樹平衡一些，方差比較大說明這個維度上的區間分布比較均勻，標示點并沒有集中在平均值附近，這樣切割的時候就不會一下 子切掉一大塊，從而錯過了可能比較接近最終答案的那些區域(最終結果的逼近原則：切割粒度盡可能小，一定要小心翼翼，類似削梨或者削鉛筆那樣的)。注 意，KD樹的目標并不是精確匹配，而是模糊最佳匹配，比如經典的尋找K個最接近的點。

6.Dimension Tree的維度排序

由 于深度優先匹配并不是遞歸構建的，因此不需要每一步都去計算方差從而確定切割的維度，對于深度優先匹配而言，只要確定了某個維度，那么將在這個維度上直接 切割完畢，對于三維情況而言，就是直接切成一個片，對于二維而言就是切成一根棍...對于接下來的切割就不需要再考慮這個維度了，因為在這個維度，它已經 精確到達它的區間了。因此，我們只需要找出一個維度序列就可以了。
       還是像KD樹一樣基于方差嗎？不一定。此時我們希望的是，讓Rule在各個區間分布最不平均的維度作為第一維，依次類推。這是因為，Rule分布不平均在 和下一維的Ruleset并集取交集的時候，對應區間在經過取交集計算后，出現唯一Default Rule從而導致快速失敗的可能性比較大，這就會減少孩子節點的數量，對于一棵M叉樹而言，越是剪掉靠近根的節點的孩子，越能抑制下層節點的瘋長。我們判 斷是否擴展該孩子的公式為：
 當前維度區間Ruleset & (next維度各個Ruleset的并集)
我們不好控制next 維度的各個區間Ruleset的并集，我們甚至不知道next維度是哪個，但是我們可以找到當前維度的Ruleset分布情況。舉一個最簡單的例子，有一 個維度劃分了4個區間，第一個區間的Ruleset中有10條，后三個區間中均是2條，那么僅有2條Rule的區間和別人取交集時很可能是空，這就為我們 找到了一個計算的依據，很顯然，我們這次不用KD樹的方差，而是將權值表示成一個區間數量，區間Rule的分布情況(這個變量可以用方差也可以不用)的函 數，從而算出最終的排序。最樸素的計算還是使用方差，計算每個維度區間中Rule數量的方差，取最小值為最高權值，這說明Rule在某個區間的分布比其它 區間更加集中，從而有更高的可能切掉孩子的臍帶導致“快速失敗”！

7.區間覆蓋問題

這是個問題嗎？不是問題。
       本文中，我們以區間為基準，因此就可以把Ruleset進行拆分。舉一個最簡單的例子，設置Rule1，2的區間192.168.1.0/24被設置Rule1，3區間192.168.0.0/16覆蓋，但是這不是問題，解決如下圖所示：

8.Dimension Tree并行匹配

不要在一棵樹上吊死！
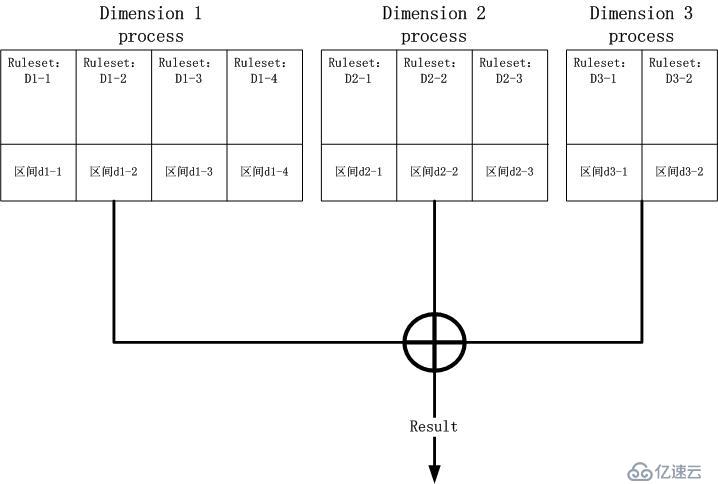
       我們非要將整個匹配數據結構塞到一棵樹中嗎？如果非要這么做，我們就失去了并行操作的可能性，因為一棵樹的從根到葉子的路徑只有一條路徑，鑒于下層分支巨 量，瞎猜只是掰扯，你幾乎不可能猜對分支。那么怎么辦呢？由于最終的結果是N個維度(在我們的例子中，N為3)的匹配區間Ruleset取交集，那么就好 辦了，N個維度分別構建N棵樹，N個處理進程同時運算，最終取交集。讓我們回到最初的那幅圖，點一下題：