您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章的內容主要圍繞如何分析Python數據結構與算法中的順序表進行講述,文章內容清晰易懂,條理清晰,非常適合新手學習,值得大家去閱讀。感興趣的朋友可以跟隨小編一起閱讀吧。希望大家通過這篇文章有所收獲!
線性表在計算機中的表示可以采用多種方法,采用不同存儲方法的線性表也有著不同的名稱和特點。線性表有兩種基本的存儲結構:順序存儲結構和鏈式存儲結構。本節將介紹順序存儲結構的特點以及各種基本運算的實現。
通過本節學習,應掌握以下內容:
線性表的順序存儲及實現方法
順序表基本操作的實現
利用順序表的基本操作實現復雜算法
線性表的順序存儲是把線性表的數據元素按邏輯次序依次存放在一組連續的存儲單元中,即邏輯結構上相鄰的兩個數據元素存儲在計算機內的物理存儲位置也是相鄰的,這種存儲方法為整個線性表分配一整個內存塊保存線性表的元素,借助數據元素在計算機內的物理位置表示線性表中數據元素之間的邏輯關系。采用順序存儲結構表示的線性表簡稱順序表 (Sequential List)。
順序表具有以下兩個基本特點:
順序表的所有元素所占的存儲空間是連續的;
順序表中各數據元素在存儲空間中是按邏輯順序依次存放的。
由于線性表的所有數據元素屬于同一數據類型,所以每個元素占用的空間(字節數)相同。因此,要在此結構中查找某一個元素是很方便的,即只要知道順序表首地址和每個數據元素在內存所占字節的大小,就可求出第 i ii 個數據元素的地址。通過使用特定元素的序號,可以在常數時間內訪問數據元素,因此可以說順序表具有按數據元素的序號隨機存取的特點。
假設線性表中的第一個數據元素的存儲地址(即順序表第一個字節的地址,也稱首地址)為id(a1),每一個數據元素占k個字節,則線性表中第i個元素ai在計算機中的存儲地址為:
id(ai)=id(a1)+(i−1)×k (1≤i≤n)
從上式可以看出,訪問順序表數據元素的過程只需要一次乘法和一次加法。由于這兩個操作只需要常數時間,因此可以說順序表訪問可以在常數時間內進行。
也就是說,順序表中的每一個數據元素在計算機存儲空間中的存儲地址由該元素在線性表中的序號惟一確定。假設有一長度為n的線性表 (a1,a2,...,an),那么其在計算機中的順序存儲結構可以用下圖表示:
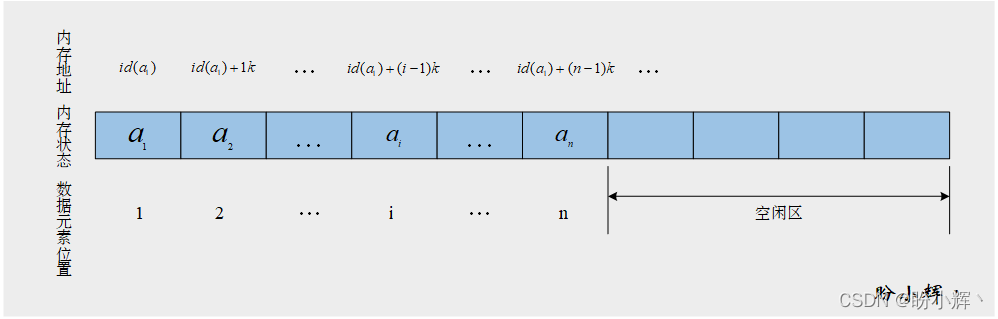
順序表的優點:
簡單易用
可以快速訪問元素
順序表的缺點:
固定大小:順序表的大小是靜態的(使用前需要指定順序表大小)
基于位置插入元素較復雜:要在給定位置插入元素,可能需要移動現有元素來創建一個空位置,以便在所需位置插入新元素;如果要在開頭添加元素,那么移位操作的開銷就更大了
為了解決順序表具有固定大小的缺陷,動態順序表的概念被提出。
動態順序表(也稱為可增長順序表、可調整大小的順序表、動態表)是一種隨機訪問、大小可變的順序表數據結構,允許添加或刪除元素,Python 內置的 list 就是一種動態順序表。
實現動態順序表的一種簡單方法是從一些固定大小的順序表開始。一旦該順序表變滿,就創建高于原始順序表大小的新順序表;同樣,如果順序表中的元素過少,則將縮小順序表大小。
接下來,為了更好的理解順序表,我們將使用 Python 實現順序表。
在具體實現時,使用 Python 中的列表來對應連續的存儲空間。設最多可存儲 max_size 個元素,為保存線性表的長度需定義一個整型變量 num_items。由于,Python 列表中索引從 0 開始,因此,線性表的第i(1≤i≤n)個元素存放在列表索引為i−1的列表元素中,為保持一致性,我們實現的順序表的序號同樣從 0 開始(也可以根據需要索引從 1 開始,只需要進行簡單修改)。
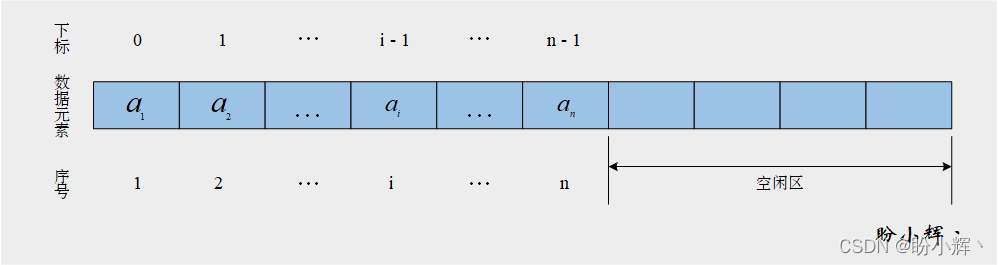
順序表的初始化需要三部分信息:items 列表用于存儲數據元素,max_size 用于存儲 items 列表的最大長度,以及 num_items 用于記錄 items 列表的當前使用的位置,即順序表中的數據元素數量。
class SequentialList: def __init__(self, max_size=10): self.items = [None] * max_size self.num_items = 0 self.max_size = max_size
初始化代碼通過創建一個包含 10 個 None 值的列表來構建一個 SequentialList 對象,內部 items 列表的初始大小 max_size 默認為 10,也可以傳遞更大的順序表大小作為初始大小,該列表也可以在需要時會動態增長。創建 SequentialList 對象的時間復雜度為O(1)。
如下圖所示,是一個包含 5 個數據元素的 SequentialList 對象:
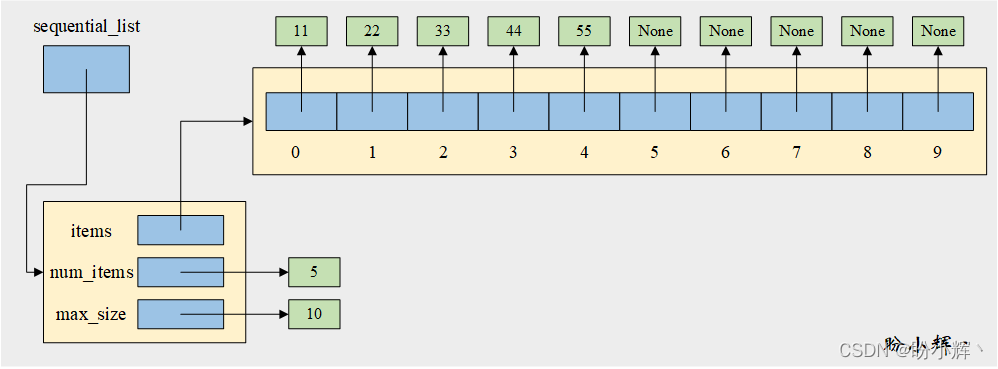
這里所說的順序表長度,指順序表中數據元素的個數,由于我們在順序表中使用 num_items 跟蹤順序表中的項數,求取順序表長度只需要重載 __len__ 從對象返回 num_items 的值,因此時間復雜度為O(1):
def __len__(self): return self.num_items
如果在 SequentialList 對象中沒有跟蹤列表的項數,那么計算順序表長度的時間復雜度為O(n)。
為了實現讀取順序表指定位置元素的操作,我們將重載 __getitem__ 操作,操作的復雜度為O(1)。同時,我們希望確保索引在可接受的索引范圍內,否則將像內置列表類一樣引發 IndexError 異常:
def __getitem__(self, index):
if index >= 0 and index < self.num_items:
return self.items[index]
raise IndexError('SequentialList index out of range')我們也可以實現修改指定位置元素的操作,只需要重載 __setitem__ 操作,其復雜度同樣為O(1):
def __setitem__(self, index, val):
if index >= 0 and index < self.num_items:
self.items[index] = val
return
raise IndexError("SequentialList assignment index out of range")要確定值為 x 的元素在順序表中的位置,需要依次比較各元素。當查詢到第一個滿足條件的數據元素時,返回其下標,否則像內置列表類一樣引發 ValueError 異常,表示查找失敗。
def locate(self, item):
for i in range(self.num_items):
if self.items[i] == item:
return i
raise ValueError("{} is not in sequential list".format(item))在查找過程中,數據元素比較次數的平均值為(n+1)/2,因此時間復雜度為O(n)。
實現在指定位置插入新元素之前,我們首先看下如何在順序表末尾追加元素。追加時,如果有空閑空間,只需要在 self.items 列表的末尾再添加一項,而當 self.items 列表填滿時,我們必須增加 self.items 列表的大小,為需要追加的新元素創建空間,創建的新 self.items 大小與 self.items 的當前長度成正比。
為了使追加操作在O(1)時間內運行,我們不能在每次需要更多空間時僅增加一個空閑位置,事實證明,每次增加 25% 的空間就足以保證O(1)復雜度。選擇增加空間的百分比并不重要,每次增加 10% 或100%的空間,同樣可以使時間復雜度為O(1)。這里選擇 25% 的原因是可以在不占用太多計算機內存的情況下多次使用追加操作擴展列表。
def __alloc(self): new_size = (self.max_size // 4) + self.max_size + 1 new_items = [None] * new_size for i in range(self.num_items): new_items[i] = self.items[i] self.items = new_items self.max_size = new_size def append(self, item): if self.num_items == self.max_size: self.__alloc() self.items[self.num_items] = item self.num_items += 1
要插入新數據元素到順序表中,必須為新元素騰出空間,下圖表示順序表中的列表在進行插入操作前后,其數據元素在列表中下標的變化情況:
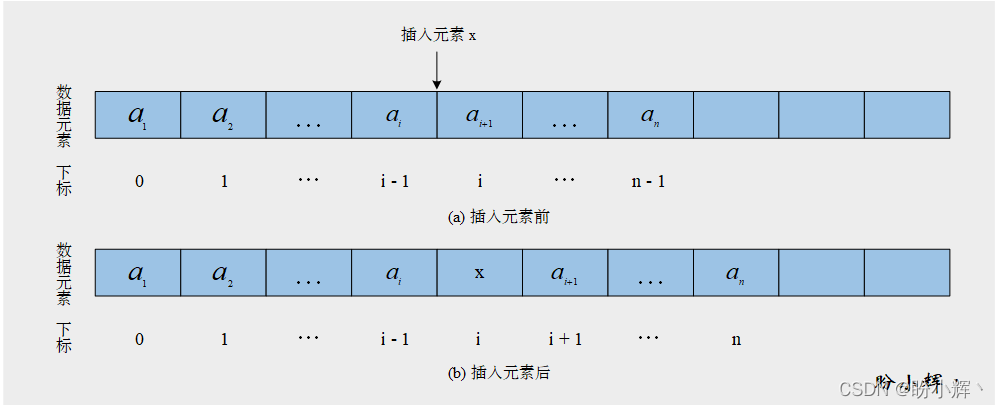
完成如上的插入操作要經過如下步驟:
1.線性表中指定位置及其之后的元素,依次向后移動一個位置,空出索引為i的位置
2.數據元素 x 插入到第i個存儲位置
3.插入結束后使線性表的長度增加 1
需要注意的是,如果線性表空間已滿,首先需要分配新的空間。如果提供的索引大于列表的大小,則將新項 x 附加到列表的末尾。插入時間元素操作的時間復雜度為O(n)。
def insert(self, index, item):
if self.num_items == self.max_size:
self.__alloc()
if index < self.num_items and index >= 0:
for j in range(self.num_items-1, index-1, -1):
self.items[j+1] = self.items[j]
self.items[index] = item
self.num_items += 1
elif index >= self.num_items:
self.append(item)
else:
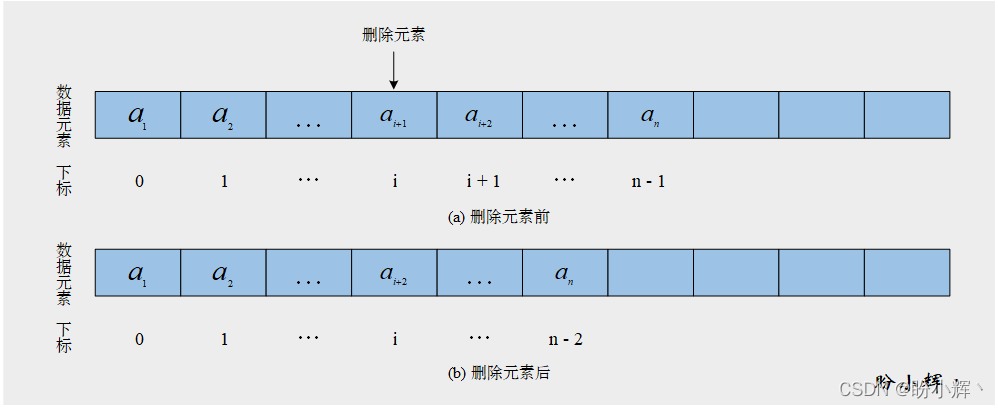
raise IndexError("SequentialList assignment index out of range")當刪除列表中特定索引處的數據元素時,我們必須將其之后的所有元素向下移動以保證內部列表中沒有無效數據。下圖表示一個順序表在進行刪除運算前后,其數據元素下標的變化:
在線性表上完成上述操作需要以下步驟:
1.在線性表中刪除下標為i的元素,從索引為i+1到n−1的元素依次向前移動依次向前移動一個位置,將所刪除的索引為i的數據元素ai+1覆蓋掉,從而保證邏輯上相鄰的元素物理位置也相鄰
2.修改順序表長度,使其減 1
為了實現刪除順序表指定位置元素的操作,我們將重載 __getitem__ 操作,在順序表上刪除數據元素時大約需要移動表中一半的元素,顯然該算法的時間復雜度為O(n)。
def __delitem__(self, index): for i in range(index, self.num_items-1): self.items[i] = self.items[i+1] self.num_items -= 1
為了更好的使用順序表,接下來將介紹其它一些很有用的操作。
例如,將順序表轉換為字符串以便進行打印,使用 str 函數調用對象上的 __str__ 方法可以創建適合打印的字符串表示,__str__ 的返回結果的可讀性很強:
def __str__(self): s = '[' for i in range(self.num_items): s += repr(self.items[i]) if i < self.num_items - 1: s += ', ' s += ']' return s
我們也可以重載成員資格函數 __contain__ 來檢查一個數據元素是否是順序表中的元素之一。這樣做的唯一方法是按順序檢查順序表中的每個數據元素。如果找到該項目,則返回 True,否則返回 False 這種搜索方法稱為線性搜索,之所以這樣命名是因為它具有O(n)的時間復雜度:
def __contains__(self, item): for i in range(self.num_items): if self.items[i] == item: return True return False
檢查兩個順序表的相等性首先需要兩個順序表的類型相同以及兩個順序表必須具有相同的長度。在滿足這兩個先決條件的情況下,如果兩個表中的所有元素都相等,則我們可以說兩個順序表相等,相等測試的時間復雜度為O(n),我們重載 __eq__ 方法實現此操作:
def __eq__(self, another): if type(another) != type(self) or self.num_items != another.num_items: return False for i in range(self.num_items): if self.items[i] != another.items[i]: return False return True
接下來,我們首先對上述實現的順序表進行測試,以驗證操作的有效性,然后利用實現的基本操作來實現更復雜的算法。
首先初始化一個順序表 sample_sqlist,并在其中追加若干元素:
sample_sqlist = SequentialList() sample_sqlist.append(11) sample_sqlist.append(22) sample_sqlist.append(33)
我們可以直接打印順序表中的數據元素、順序表長度等信息:
print('順序表數據元素為:', sample_sqlist)
print('順序表長度:', len(sample_sqlist))
print('順序表中第0個數據元素:', sample_sqlist[0])
# 修改數據元素
sample_sqlist[1] = 2022
print('順序表數據元素為:', sample_sqlist)以上代碼輸出如下:
順序表數據元素為: [11, 22, 33]
順序表長度: 3
順序表中第0個數據元素: 11
順序表數據元素為: [11, 2022, 33]
接下來,我們將演示在指定位置添加/刪除元素、以及如何查找指定元素等:
print('在順序表位置1處添加元素2021')
sample_sqlist.insert(1, 2021)
print('添加元素后,順序表數據元素為:', sample_sqlist)
print('刪除順序表位置2處元素')
del(sample_sqlist[2])
print('刪除數據后,順序表數據元素為:', sample_sqlist)
print('元素11的索引為{}'.format(sample_sqlist.locate(11)))
print('11在順序表中?', 11 in sample_sqlist)
print('22在順序表中?', 22 in sample_sqlist)以上代碼輸出如下:
在順序表位置1處添加元素2021
添加元素后,順序表數據元素為: [11, 2021, 2022, 33]
刪除順序表位置2處元素
刪除數據后,順序表數據元素為: [11, 2021, 33]
元素11的索引為0
11在順序表中? True
22在順序表中? False
[1] 利用順序表的基本操作,合并兩個順序表:
def add_sqlist(sqlist1, sqlist2):
result = SequentialList(max_size=sqlist1.num_items+sqlist2.num_items)
for i in range(sqlist1.num_items):
result.append(sqlist1[i])
for i in range(sqlist2.num_items):
result.append(sqlist2[i])
return result
# 算法測試
sqlist1 = SequentialList()
sqlist2 = SequentialList()
for i in range(10):
sqlist1.append(i)
sqlist2.append(i*5)
print('順序表1:', sqlist1, '順序表2:', sqlist2)
# 合并順序表
result = add_sqlist(sqlist1, sqlist2)
print('合并順序表:', result)可以看到合并兩個順序表的時間復雜度為O(n),程序輸出結果如下:
順序表1: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] 順序表2: [0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
合并順序表: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
[2] 利用順序表 sqlist1 和 sqlist2 中公共數據元素生成新順序表:
def commelem(sqlist1, sqlist2):
result = SequentialList()
for i in range(sqlist1.num_items):
if sqlist1[i] in sqlist2 and sqlist1[i] not in result:
result.append(sqlist1[i])
return result
# 算法測試
sqlist1 = SequentialList()
sqlist2 = SequentialList()
for i in range(5):
sqlist1.append(i*2)
sqlist1.append(i)
sqlist2.append(i*3)
print('順序表1:', sqlist1, '順序表2:', sqlist2)
# 合并順序表
result = commelem(sqlist1, sqlist2)
print('兩順序表中的公共元素:', result)可以看到算法的時間復雜度為O(n2),程序輸出結果如下:
合并順序表: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]
順序表1: [0, 0, 2, 1, 4, 2, 6, 3, 8, 4] 順序表2: [0, 3, 6, 9, 12]
兩順序表中的公共元素: [0, 6, 3]
感謝你的閱讀,相信你對“如何分析Python數據結構與算法中的順序表”這一問題有一定的了解,快去動手實踐吧,如果想了解更多相關知識點,可以關注億速云網站!小編會繼續為大家帶來更好的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。