您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“R語言多元線性回歸怎么實現”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
⑴多元回歸模型建立
#讀取物種和環境因子信息data=read.csv("otu_table.csv", header=TRUE, row.names=1)otu=t(data)envir=read.table("environment.txt", header=TRUE)rownames(envir)=envir[,1]env=envir[,-1]#計算alpha多樣性library(vegan)shannon=diversity(otu, index="shannon")biodata=data.frame(shannon, env[,c("Salinity", "pH", "TN", "TP")])fit=lm(shannon~Salinity+pH+TN+TP, data=biodata)summary(fit)
回歸結果如下所示:

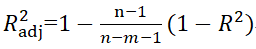
上式被稱為Ezekiel公式。上面多元回歸的結果中已經給出了校正后的R2(51%),我們也可以使用vegan包中的RsquareAdj()函數來校正類多元回歸模型(MLR、RDA等)中的R2,如下所示:
library(vegan)RsquareAdj(fit)
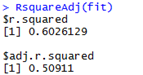
在上面的多元回歸分析中,并沒有考慮交互項,但是交互項的解釋模型往往使得研究更加有趣,交互影響說明兩個解釋變量對響應變量的影響是非獨立的,例如兩種重金屬濃度升高時造成的毒性大于單獨存在時的毒性,如下所示:
fit2=lm(shannon~Salinity+TN+TP:pH, data=biodata)summary(fit2)
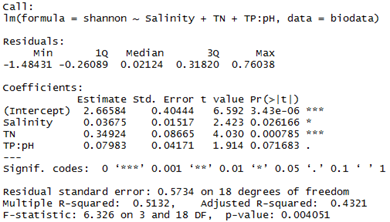
可以看到,使用TP與pH的交互項作為一個預測變量后,系數的顯著性整體增強,而在第一次回歸中,TP與多樣性系數不顯著,交互項可以理解為TP對多樣性的影響要依賴于pH的水平,也即不同pH下TP對微生物群落的影響不同。復雜的多重多元線性回歸可以使用RDA分析來實現。
⑵回歸診斷
我們可以使用一元回歸診斷方法進行簡單的診斷,結果如下:
par(mfrow=c(2,2))plot(fit)
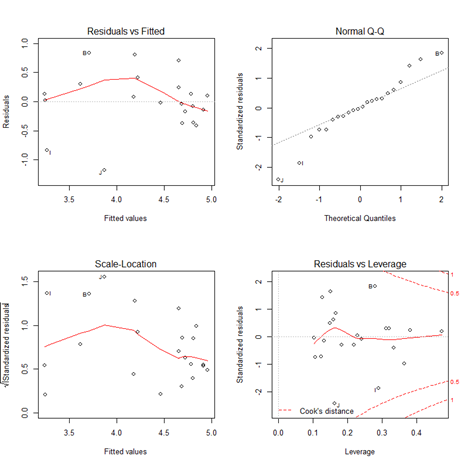
在R中car包提供了更詳細的回歸模型診斷函數,接下來我們對多元回歸模型進行詳細的評價。
①正態性
可以通過檢驗殘差是否滿足t分布來檢驗正態性,如下所示:
library(car)par(mfrow=c(1,1))qqPlot(fit, labels=names(shannon), id.method="identify", simulate=TRUE)
其中simulate=TRUE則95%的置信區間會使用參數自助法(parametric bootstrap)生成,自助法就是假設樣本是總體,然后采取有放回抽樣方法來確定參數的分布。如下圖所示,沒有觀察到超出置信區間的離群點,也即數據正態性良好:
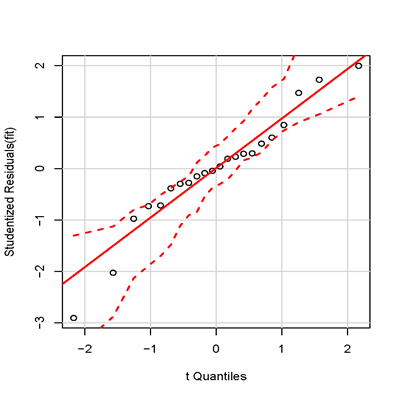
②殘差獨立性
接下來檢驗殘差是否相關,可以使用durbinWatsonTest()函數進行Durbin-Waston檢驗,如下所示:
durbinWatsonTest(fit, simulate=TRUE, reps=999)

其中參數reps設置了自助抽樣的次數,結果p值剛好大于0.05,可以拒絕零假設也即殘差相關,說明殘差是獨立的。不過這個p值很小,仍是有不獨立可能的,可以想象,多樣性指數越低那么誤差范圍越小,預測值與觀察值越接近,因此殘差可能存在不獨立性。
③線性
因變量與自變量是否具有線性關系可以通過成分殘差圖來檢驗,方法如下:
crPlots(fit)
如下圖所示,成分殘差圖以每一個預測變量作為橫坐標,以整體模型的殘差加該預測變量和其系數的乘積(也即擬合值中該變量承擔的部分)作為縱坐標,如果所有圖像均為線性,說明線性關系良好;如果某一變量成分殘差圖為非線性,說明該變量需要添加多項式項。
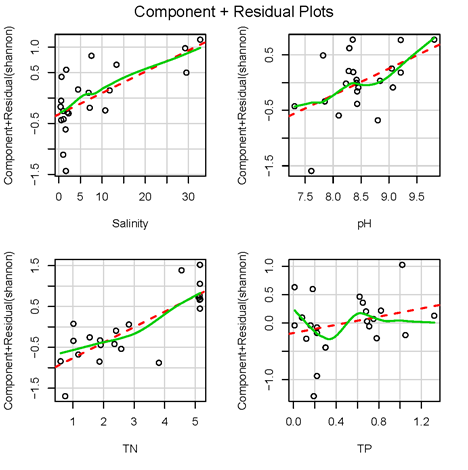
④同方差性
可以使用ncvTest()函數檢驗方差恒定性,如下所示:
ncvTest(fit)

改檢驗零假設是誤差恒定,p值大于0.05同方差性檢驗通過。此外,spreadLevelPlot()函數繪制殘差與擬合值的關系圖,并給出數據轉換建議:
spreadLevelPlot(fit)

如下圖所示,隨著擬合值的變化先增大后減小(根據實際情況,這很可能是由于變量不均勻性造成的),檢驗結果給出的建議是對響應變量數據進行2.59次冪次變換(即power transformation)。
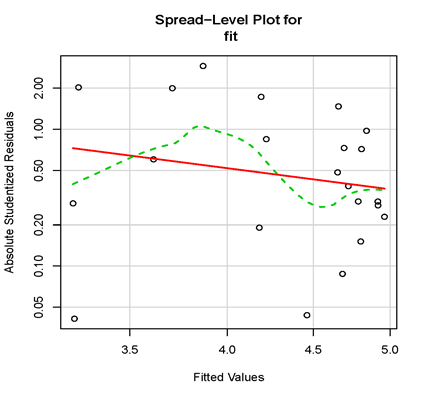
⑤多重共線性
在使用多個解釋變量進行回歸建模時,有時整個模型的顯著性非常好,然而回歸系數的檢驗卻不顯著,這時候很可能出現了多重共線性問題,也即解釋變量之間存在較強的相關性。由于回歸系數測量的實際上是固定其他解釋變量時該解釋變量對因變量的影響,共線性會導致回歸參數的置信區間過大,是單個系數解釋起來很困難。
在生態分析中,環境因子之間很可能會存在共線性問題,這對RDA、CCA、CAP等基于多元回歸的模型來說非常重要,因為這些方法使用到了回歸系數作為衡量解釋變量影響的指標,而VPA分析若要檢驗每部分方差的顯著性也需要消除共線性,LDA分析同樣如此。在3.3.2.1RDA分析中我們使用了統計量VIF(variance inflation factor,方差膨脹因子)進行檢測,VIF實際上衡量的是回歸參數的置信區間能膨脹為與模型無關的解釋變量的程度,一般VIF>4則認為存在多重共線性問題,檢驗方法如下:
vif(fit)

從結果可以看出,共線性問題并不嚴重。
⑥篩選特殊點
響應變量中模型預測效果不佳的點稱之為離群點,預測變量中異常的預測變量值為高杠桿值點,對模型參數影響過大的點稱之為強影響點,也即移除這一觀測點模型會發生巨大的改變。對于一個模型來說,我們自然希望每個點影響是一樣的,一般來說強影響點既是離群點又是高杠桿值點。在前面的診斷中,已經初步涉及了離群點和高杠桿點的檢測,下面提供一些其他的檢測方法:
#檢測離群點(校正后p值小于0.05為離群點)outlierTest(fit)

#可視化方法檢測特殊點influencePlot(fit, id.method="identify", ylim=c(-3,3))
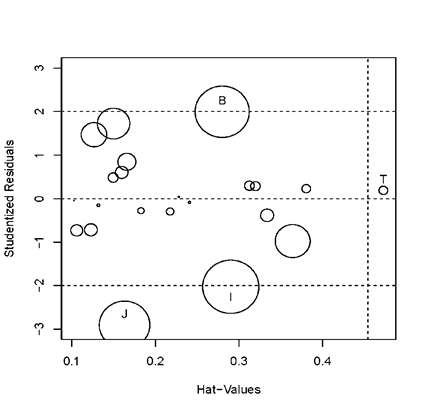
上圖橫坐標為帽子統計量,越大則杠桿值越大,縱軸為殘差,其絕對值越大則越可能為離群點,圓圈越大則該點影響力越大。
“R語言多元線性回歸怎么實現”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。