您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關Python中多元線性回歸的示例分析,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
1.觀察數據
首先,用Pandas打開數據,并進行觀察。
import numpy
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
data = pd.read_csv('Folds5x2_pp.csv')
data.head()會看到數據如下所示:
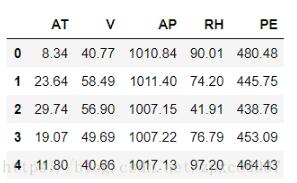
這份數據代表了一個循環發電廠,每個數據有5列,分別是:AT(溫度), V(壓力), AP(濕度), RH(壓強), PE(輸出電力)。我們不用糾結于每項具體的意思。
我們的問題是得到一個線性的關系,對應PE是樣本輸出,而AT/V/AP/RH這4個是樣本特征, 機器學習的目的就是得到一個線性回歸模型,即: PE=θ0+θ1?AT+θ2?V+θ3?AP+θ4?RH 而需要學習的,就是θ0,θ1,θ2,θ3,θ4這5個參數。
接下來對數據進行歸一化處理:
data = (data - data.mean())/data.std()
因為回歸線的截距θ0是不受樣本特征影響的,因此我們在此可以設立一個X0=1,使得回歸模型為:
PE=θ0*X0+θ1?AT+θ2?V+θ3?AP+θ4?RH
將方程向量化可得:
PE = hθ(x) = θx (θ應轉置)
2.線性回歸
在線性回歸中,首先應建立 cost function,當 cost function 的值最小時所取得θ值為所求的θ。
在線性回歸中,Cost function如下所示:
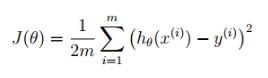
因此,可以在Python中建立函數求損失方程:
def CostFunction(X,y,theta): inner = np.power((X*theta.T)-y,2) return np.sum(inner)/(2*len(X))
然后,設初始θ為=[0,0,0,0,0],可得到最初的J(θ)值為0.49994774247491858,代碼如下所示
col = data.shape[1] X = data.iloc[:,0:col-1] y = data.iloc[:,col-1:col] X = np.matrix(X.values) y = np.matrix(y.values) theta = np.matrix(np.array([0,0,0,0,0])) temp = np.matrix(np.zeros(theta.shape)) CostFunction(X,y,theta)
接下來,有兩種方法可以使用。1.梯度下降法(gradient descent)和 2.最小二乘法(normal equation)。在此我們使用梯度下降法來求解。
梯度下降法是求得J對θ的偏導數,通過設置步長,迭代使J(θ)逐步下降,從而求得局部最優解。
公式如下所示:
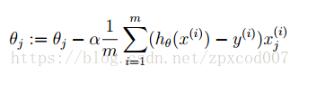
j:特征編號
m:樣本編號
我們可以在Python中寫出計算迭代后的θ和J(θ)
def gradientDescent(X,y,theta,alpha,iters): temp = np.matrix(np.zeros(theta.shape)) parameters = int(theta.ravel().shape[1]) cost = np.zeros(iters) for i in range(iters): error = (X*theta.T)-y for j in range(parameters): term = np.multiply(error,X[:,j]) temp[0,j] = theta[0,j] - (alpha/len(X))*np.sum(term) theta = temp cost[i] = CostFunction(X,y,theta) return theta,cost
在此,我設置初始的α為0.1,可求得迭代1000次后θ0,θ1,θ2,θ3,θ4的值分別是:
-5.22080706e-14,-8.63485491e-01,-1.74182863e-01,2.16058120e-02,-1.35205248e-01
此時 J(θ)的值為0.0379648。
通過,可視化J(θ)和迭代次數可以發現,J(θ)收斂的非常快。
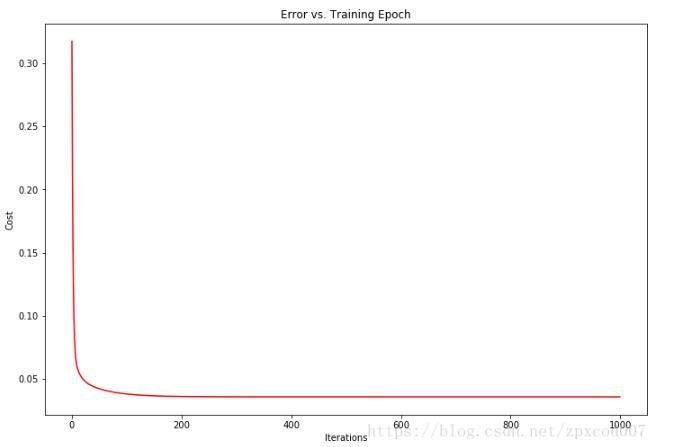
畫圖觀察預測值和損失值,距離直線約近說明損失越小:
predicted = X*g.T
predicted = predicted.flatten().A[0]
y_f= y.flatten().A[0]
fig, ax = plt.subplots()
ax.scatter(y_f,predicted)
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()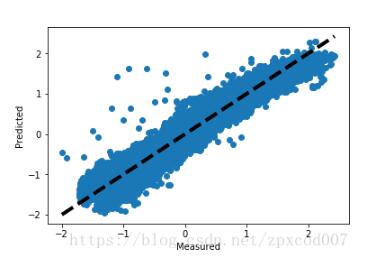
3.sckit-learn
因為J(θ)收斂的太快了…所以我又用sckit-learn和SPSS驗證了一下。
先看sckit-learn,在sklearn中,線性回歸是使用的最小二乘法而不是梯度下降法,用起來也十分的簡單。
代碼如下:
from sklearn import linear_model model = linear_model.LinearRegression() model.fit(X, y)
打印出θ值后發現和梯度下降法算出來的相差無幾,θ0,θ1,θ2,θ3,θ4的值分別是:
0,-0.86350078,-0.17417154,0.02160293,-0.13521023
4.SPSS
在看看SPSS
同樣先將數據標準化后進行線
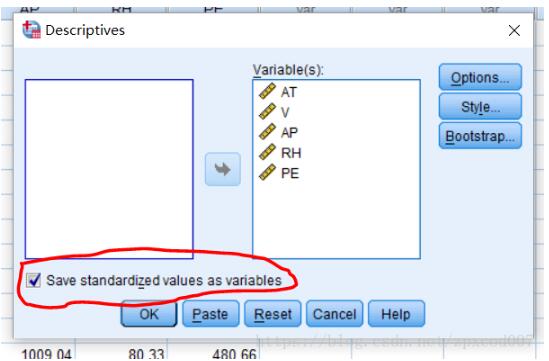
然后進行線性回歸分析得到結果:
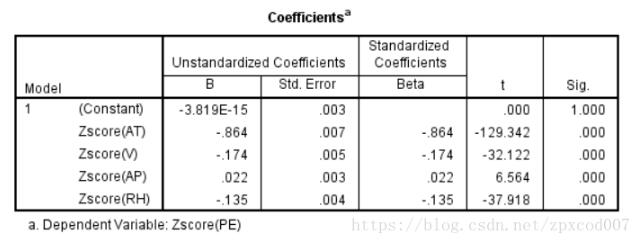
關于“Python中多元線性回歸的示例分析”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,使各位可以學到更多知識,如果覺得文章不錯,請把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。