您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章為大家展示了怎么使用scikit-learn工具來進行PCA降維,內容簡明扼要并且容易理解,絕對能使你眼前一亮,通過這篇文章的詳細介紹希望你能有所收獲。
1. scikit-learn PCA類介紹
在scikit-learn中,與PCA相關的類都在sklearn.decomposition包中。最常用的PCA類就是sklearn.decomposition.PCA,我們下面主要也會講解基于這個類的使用的方法。
除了PCA類以外,最常用的PCA相關類還有KernelPCA類,在原理篇我們也講到了,它主要用于非線性數據的降維,需要用到核技巧。因此在使用的時候需要選擇合適的核函數并對核函數的參數進行調參。
另外一個常用的PCA相關類是IncrementalPCA類,它主要是為了解決單機內存限制的。有時候我們的樣本量可能是上百萬+,維度可能也是上千,直接去擬合數據可能會讓內存爆掉, 此時我們可以用IncrementalPCA類來解決這個問題。IncrementalPCA先將數據分成多個batch,然后對每個batch依次遞增調用partial_fit函數,這樣一步步的得到最終的樣本最優降維。
此外還有SparsePCA和MiniBatchSparsePCA。他們和上面講到的PCA類的區別主要是使用了L1的正則化,這樣可以將很多非主要成分的影響度降為0,這樣在PCA降維的時候我們僅僅需要對那些相對比較主要的成分進行PCA降維,避免了一些噪聲之類的因素對我們PCA降維的影響。SparsePCA和MiniBatchSparsePCA之間的區別則是MiniBatchSparsePCA通過使用一部分樣本特征和給定的迭代次數來進行PCA降維,以解決在大樣本時特征分解過慢的問題,當然,代價就是PCA降維的精確度可能會降低。使用SparsePCA和MiniBatchSparsePCA需要對L1正則化參數進行調參。
2. sklearn.decomposition.PCA參數介紹
下面我們主要基于sklearn.decomposition.PCA來講解如何使用scikit-learn進行PCA降維。PCA類基本不需要調參,一般來說,我們只需要指定我們需要降維到的維度,或者我們希望降維后的主成分的方差和占原始維度所有特征方差和的比例閾值就可以了。
現在我們對sklearn.decomposition.PCA的主要參數做一個介紹:
1)n_components:這個參數可以幫我們指定希望PCA降維后的特征維度數目。最常用的做法是直接指定降維到的維度數目,此時n_components是一個大于等于1的整數。當然,我們也可以指定主成分的方差和所占的最小比例閾值,讓PCA類自己去根據樣本特征方差來決定降維到的維度數,此時n_components是一個(0,1]之間的數。當然,我們還可以將參數設置為"mle", 此時PCA類會用MLE算法根據特征的方差分布情況自己去選擇一定數量的主成分特征來降維。我們也可以用默認值,即不輸入n_components,此時n_components=min(樣本數,特征數)。
2)whiten :判斷是否進行白化。所謂白化,就是對降維后的數據的每個特征進行歸一化,讓方差都為1.對于PCA降維本身來說,一般不需要白化。如果你PCA降維后有后續的數據處理動作,可以考慮白化。默認值是False,即不進行白化。
3)svd_solver:即指定奇異值分解SVD的方法,由于特征分解是奇異值分解SVD的一個特例,一般的PCA庫都是基于SVD實現的。有4個可以選擇的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般適用于數據量大,數據維度多同時主成分數目比例又較低的PCA降維,它使用了一些加快SVD的隨機算法。 full則是傳統意義上的SVD,使用了scipy庫對應的實現。arpack和randomized的適用場景類似,區別是randomized使用的是scikit-learn自己的SVD實現,而arpack直接使用了scipy庫的sparse SVD實現。默認是auto,即PCA類會自己去在前面講到的三種算法里面去權衡,選擇一個合適的SVD算法來降維。一般來說,使用默認值就夠了。
除了這些輸入參數外,有兩個PCA類的成員值得關注。第一個是explained_variance,它代表降維后的各主成分的方差值。方差值越大,則說明越是重要的主成分。第二個是explained_variance_ratio_,它代表降維后的各主成分的方差值占總方差值的比例,這個比例越大,則越是重要的主成分。
3. PCA實例
下面我們用一個實例來學習下scikit-learn中的PCA類使用。為了方便的可視化讓大家有一個直觀的認識,我們這里使用了三維的數據來降維。
首先我們生成隨機數據并可視化,代碼如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from sklearn.datasets.samples_generator import make_blobs
# X為樣本特征,Y為樣本簇類別, 共1000個樣本,每個樣本3個特征,共4個簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]], cluster_std=[0.2, 0.1, 0.2, 0.2],
random_state =9)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o')
三維數據的分布圖如下:

我們先不降維,只對數據進行投影,看看投影后的三個維度的方差分布,代碼如下:
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
輸出如下:
[ 0.98318212 0.00850037 0.00831751]
[ 3.78483785 0.03272285 0.03201892]
可以看出投影后三個特征維度的方差比例大約為98.3%:0.8%:0.8%。投影后第一個特征占了絕大多數的主成分比例。
現在我們來進行降維,從三維降到2維,代碼如下:
pca = PCA(n_components=2)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
輸出如下:
[ 0.98318212 0.00850037]
[ 3.78483785 0.03272285]
這個結果其實可以預料,因為上面三個投影后的特征維度的方差分別為:[ 3.78483785 0.03272285 0.03201892],投影到二維后選擇的肯定是前兩個特征,而拋棄第三個特征。
為了有個直觀的認識,我們看看此時轉化后的數據分布,代碼如下:
X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1],marker='o')
plt.show()
輸出的圖如下:
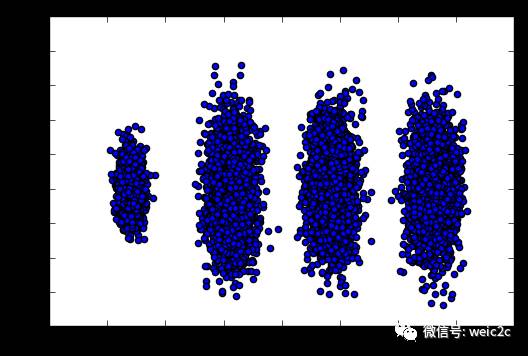
可見降維后的數據依然可以很清楚的看到我們之前三維圖中的4個簇。
現在我們看看不直接指定降維的維度,而指定降維后的主成分方差和比例。
pca = PCA(n_components=0.95)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
print pca.n_components_
我們指定了主成分至少占95%,輸出如下:
[ 0.98318212]
[ 3.78483785]
1
可見只有第一個投影特征被保留。這也很好理解,我們的第一個主成分占投影特征的方差比例高達98%。只選擇這一個特征維度便可以滿足95%的閾值。我們現在選擇閾值99%看看,代碼如下:
pca = PCA(n_components=0.99)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
print pca.n_components_
此時的輸出如下:
[ 0.98318212 0.00850037]
[ 3.78483785 0.03272285]
2
這個結果也很好理解,因為我們第一個主成分占了98.3%的方差比例,第二個主成分占了0.8%的方差比例,兩者一起可以滿足我們的閾值。
最后我們看看讓MLE算法自己選擇降維維度的效果,代碼如下:
pca = PCA(n_components='mle')
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_
print pca.n_components_
輸出結果如下:
[ 0.98318212]
[ 3.78483785]
1
可見由于我們的數據的第一個投影特征的方差占比高達98.3%,MLE算法只保留了我們的第一個特征。
上述內容就是怎么使用scikit-learn工具來進行PCA降維,你們學到知識或技能了嗎?如果還想學到更多技能或者豐富自己的知識儲備,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。