您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關大數據中正則化是什么意思的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
通過設計不同層數、大小的網絡模型,可以為優化算法提供初始的函數假設空間(或者所示網絡容量)。但是隨著網絡參數的優化更新,模型的實際容量是可以隨之變化的。
以多項式函數模型為例:
y = r 0 + r 1 x + r 2 x 2 + r 3 x 3 … + r n x n + e r r o r y=r_0+r_1x+r_2x^2+r_3x^3…+r_nx^n+error y=r0+r1x+r2x2+r3x3…+rnxn+error
上述模型容量可以通過n來簡單衡量。在訓練的過程中,如果模型參數 r i = 0 r_i=0 ri=0,表征的函數模型也就降維了,那么網絡的實際容量也就相應的減小了。因此,通過限制網絡的稀疏性,可以來約束網絡的實際容量。
正則化正是通過在損失函數上添加額外的參數稀疏性懲罰項(正則項),來限制網絡的稀疏性,以此約束網絡的實際容量,從而防止模型出現過擬合。
因此,對模型的參數添加稀疏性懲罰項后,我們的目標損失函數就變為:
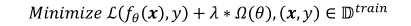
式子中的第一項為原始的損失函數,第二項是對網絡參數的稀疏性約束函數,也就是正則項。
下面我們重點來研究一下正則項。一般地,參數的稀疏性約束通過約束參數 θ \theta θ的L范數實現,即:

新的優化目標除了要最小化原來的損失函數之外,還需要約束網絡參數的稀疏性,優化算法會在降低損失函數的同時,盡可能地迫使網絡參數 θ \theta θ變得稀疏,他們之間的權重關系通過超參數????來平衡,較大的????意味著網絡的稀疏性更重要;較小的????則意味著網絡的訓練誤差更重要。通過選擇合適的????超參數可以獲得較好的訓練性能,同時保證網絡的稀疏性,從而獲得不錯的泛化能力。
常用的正則化方式有 L0,L1,L2 正則化。即0范數、1范數、2范數。
L0 正則化是指采用 L0 范數作為稀疏性懲罰項 Ω ( θ ) \Omega(\theta) Ω(θ)的正則化方式,即
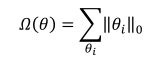
其中,L0范數定義為: θ i \theta_i θi中非零元素的個數。通過約束 Ω ( θ ) \Omega(\theta) Ω(θ)的大小,可以迫使網絡中的連接權值大部分為0。但是由于L0范數并不可導,不能利用梯度下降法進行優化,所以在神經網絡中的使用并不多。
采用 L1 范數作為稀疏性懲罰項 Ω ( θ ) \Omega(\theta) Ω(θ)的正則化方式叫做 L1 正則化,即
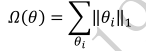
其中,L1范數定義為: θ i \theta_i θi中所有元素的絕對值之和。L1 正則化也叫 Lasso
Regularization,它是連續可導的,在神經網絡中使用廣泛。
采用 L2 范數作為稀疏性懲罰項 Ω ( θ ) \Omega(\theta) Ω(θ)的正則化方式叫做 L2 正則化,即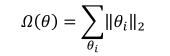
其中L2范數定義為: θ i \theta_i θi中所有元素的平方和。L2 正則化也叫Ridge Regularization,它和 L1 正則化一樣,也是連續可導的,在神經網絡中使用廣泛。
下面實驗,在維持網絡結構等其他超參數不變的條件下,在損失函數上添加L2正則化項,并通過改變超參數 λ \lambda λ來獲得不同程度的正則化效果。
實驗效果如下:
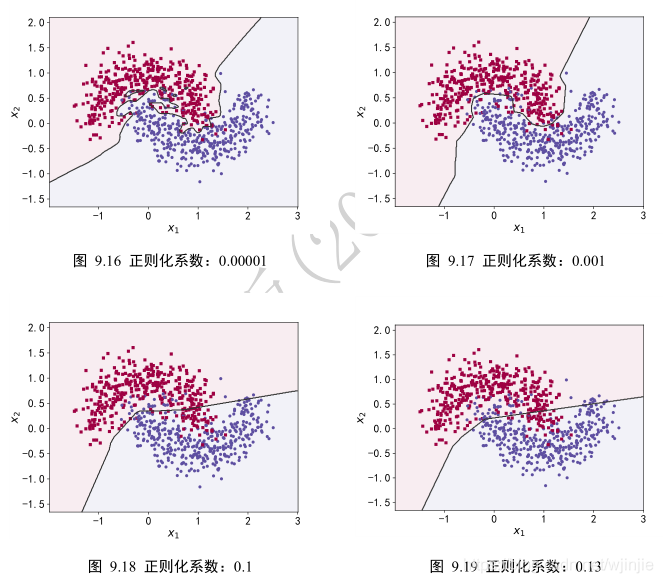
可以看到,隨著正則化系數????的增加,網絡對參數稀疏性的懲罰變大,從而迫使優化算法搜索而得到網絡容量更小的模型。在???? = 0.00001時,正則化的作用比較微弱,網絡出現了過擬合現象;但是???? = 0.1時,網絡已經能夠優化到合適的容量,并沒有出現明顯過擬合和欠擬合的現象。
需要注意的是,實際訓練時,一般先嘗試較小的正則化系數????,觀測網絡是否出現過擬合現象。然后嘗試逐漸增大????參數來增加網絡參數稀疏性,提高泛化能力。但是,過大的????
參數有可能導致網絡不收斂,需要根據實際任務調節。
感謝各位的閱讀!關于“大數據中正則化是什么意思”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。