您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“索引能提高查詢性能的原因是什么”,在日常操作中,相信很多人在索引能提高查詢性能的原因是什么問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”索引能提高查詢性能的原因是什么”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
二叉樹
由 n( n > 0)個有限節點組成一個具有層次關系的集合,看起來就像一個倒掛的樹,因此稱這樣的數據結構為樹。
一個節點的子節點個數叫做度,通俗的講就是樹叉的個數。樹中最大的度叫做樹的度,也叫做階。一個 2 階樹最多有 2 個子節點即最多有 2 叉,因此這樣的樹稱為二叉樹,二叉樹是樹家族中最簡單的樹。
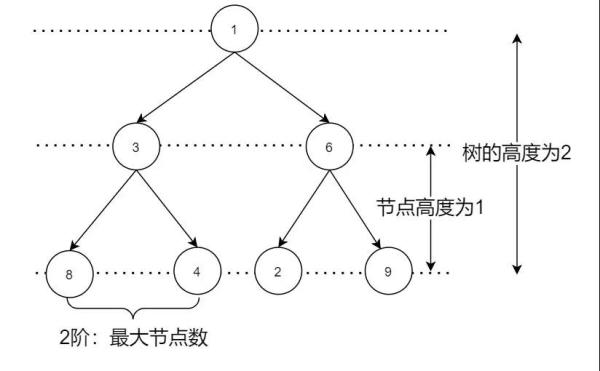
兩個叉的樹就是二叉樹,可這除了用來按一定結構存放數據外,跟查詢性能好像也沒關系,不會又是一個沒用的噱頭吧。
二分查找
聽說二叉樹的原始威力來源于一種叫做二分查找的算法。
相傳在鸚鵡的原始社會,存在著森嚴的等級制度,每只鳥必須按高矮順序分出等級和尊卑。
那么問題來了,如下圖,怎樣才能找出最高、最矮、中等高的那些鸚鵡呢、以及指定高度的那只呢?
第一種方法: 掃描法
一個一個依次測量,完畢后所有的問題都迎刃而解。
這種一個一個依次全部測量的方法叫做掃描,他的缺點很明顯,最高和最矮,需要全部測量完畢才能知曉。
而對于指定高度,最好的情況是第一次就找到;最壞的情況是最后一次才找到,時間復雜度為 n,也就是說從 13 個鸚鵡中找到指定身高的那只,最壞的情況是查 13 次。
第二種方法:二分法
13 個鸚鵡全部聽令,按從矮到高列隊,向左看齊,報數。

報數字 1 的就是最矮的,報數字 13 的就是最高的,報數字 7 的就是中等身高的那只。
最好和最壞的情況都是一次找到。而查詢性能一下子提高 13 倍,我的個乖乖,無論多個只鸚鵡,時間復雜度都是 1,好可怕。
問題:我不服,你這是偷換概念,有本事對比一個查找指定高度鸚鵡的性能。
因為鸚鵡們已經按高矮排好了隊,所以指定高度的鸚鵡,要么是站中間那個只,要么就是在它的左邊或右邊的那群里。
如果是中間那個,一次就找到,如果不是只需要從中間左邊或右邊那一半中找,再在這一半中找中間那只,對比身高。
以此類推,每次都把查詢的范圍減半,時間復雜度log2(n)。
那么 log2(13) 就是 4,最壞的情況也才 4 次,時間復雜度確實不是 1 了,但好像也不糟,簡化如下:

問題:如果按高矮排隊,仍然需要一個一個比較,跟掃描有什么區別,那還不如直接掃描呢?
事實確實如此,單純的一次查詢,先排序,再二分查找,不見得比掃描快,甚至還不如。
但是,在數據的世界,大部分數據一生會被查詢無數次,如果只在數據降生的時候排一次序,往后余生,是不是就可以直接用二分查找,這似乎就是傳說的讀多寫少,以及對應的復用。
優點:
查找快
缺點:
必須有序,需要提前排序
每次查找都需要不斷計算中間位置
二分查找樹
如果一組數據不會或不常變更,那么他們的位置也基本不變。可是每次查詢都需要重新計算中間位置是一種浪費,而浪費可恥。
我們能不能把所有中間節點組織起來,每次使用時,直接取中間節點?
請看下圖,找到所有單次二分查找的中間節點,把他們連起來,并用手提起最中間的那個節點,就是一棵二分查找樹。

優點:二分查找樹就是通過數據結構的方式實現了二分查找算法,通過存儲中間節點的數據,彌補了二分查找每次都要計算中間位置的缺點。
平衡二叉樹:
如果二分查找樹不斷進行修改,比如刪除某些節點,經過一段時間后,最早那個中間節點的數據(根),很可能就不在中間了。
中間位置就像一個天平的支點,如果他不在中間了,那么整個天平就會失衡,失衡的世界就會坍塌成不倫不類的瘸樹,甚至是降維成一個鏈表或者數組。
二分查找算法的關鍵在于有序和中間節點,而二分查找樹的關鍵是中間節點的維護,如果維護的節點已經不在中間了,那么它就失去了意義。
所以必須保證「二分查找樹」是一個正確的樹,一個根節點在中心的樹,一個左右子樹層級(高度)基本相等(高度相差不超過1)的樹,一個平衡的樹。
平衡二叉樹中最常見的就是紅黑樹:
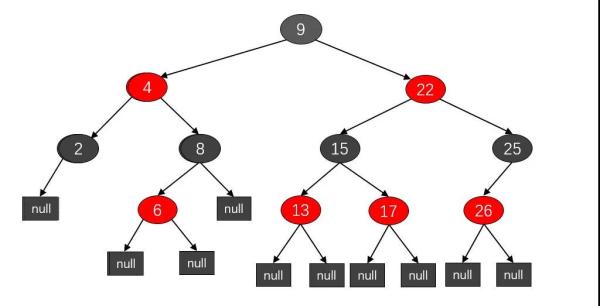
紅黑樹規定了一系列節點顏色規則,以及對應的左旋和右旋操作來保證顏色規則,從而達到樹的平衡性。
看到這花里胡哨的顏色以及復雜的規則,讓人第一眼就望而卻步,但所有的這些,也不過是為了保證二叉樹的平衡性,由于維持平衡的操作太過麻煩,無法用一句話簡單概括,只好用一堆人鬼難分的規則和步驟來實現,只要按著這些步驟就一定能實現二叉樹的平衡。
平衡二叉樹 = 二分查找樹 + 平衡(左右高度相差不超過 1 )
平衡二叉樹并未提高二分查找樹的性能,它只是保正樹不會被二向箔(多次增刪改)打擊降維成鏈表或不對稱的殘缺樹,永遠維持平衡。
另外,不僅僅是二叉樹,其他種類的樹,也是需要有序和平衡,才能發揮最大的威力。
多叉樹之 B-tree
兩個叉的樹就能折半查詢,理論可以提高一倍性能,那么多個叉是不是能提高更多倍性能?
如下圖的 3 階(叉)樹(所有數據僅用于演示,非真實分布)
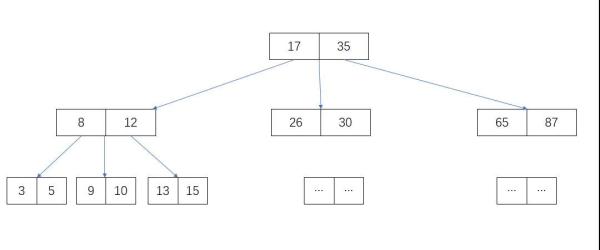
每個節點維護兩個數據,并指向最多 3 個子節點。如圖 3 個子節點的數據分別為:小于 17, 17 ~ 35 ,大于 35。
假設,從上圖中查找 10 這個數,步驟如下:
鴻蒙官方戰略合作共建——HarmonyOS技術社區
找到根節點,對比 10 與 17 和 35 的大小,發現 10 < 17 在左子節點,也就是第 2 層節點;
從根節點的指針,找到左子節點,對比 10 與 8 和 12 的大小,發現 8 < 10 < 12,數據在當前節點的中間子節點,也就是第 3 層節點;
通過上步節點的指針,找到中間子節點(第 3 層節點),對比 10 與 9 和 10 的大小,發現 9 < 10 == 10,因此找到當前節點的第二數即為結果。
加上忽略的 12 個數據,從 26 個數據中查找一個數字 10,僅僅用了 log3(26)≈ 3 次,而如果用平衡二叉樹,則需要 log2(26)≈ 5 次,事實證明,多叉樹確實可以再次提高查找性能。
多叉樹是在二分查找樹的基礎上,增加單個節點的數據存儲數量,同時增加了樹的子節點數,一次計算可以把查找范圍縮小更多。
優點:二叉平衡樹的基礎上,使加載一次節點,可以加載更多路徑數據,同時把查詢范圍縮減到更小。
復雜節點:
至此,我們列舉的數據都是孤零零的單個數字。試想,你手里已經有一個數據 10,為什么還要費力吧唧的再從一堆數據中找到這個 10,自己找自己?這不是有病嗎?
單個數字只能活在演示中,現實的世界要復雜的多,我們來看一個接近真實場景的案例。
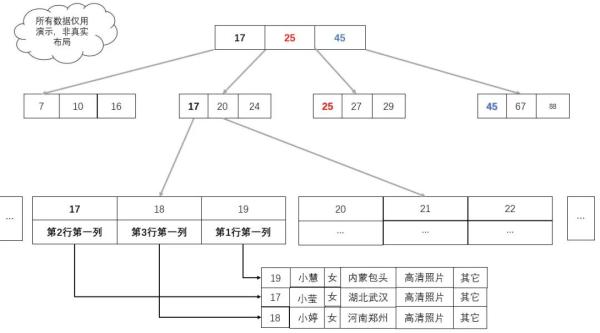
現有一個以年齡為索引的 3 階樹,存儲了一批用戶信息,如下圖:
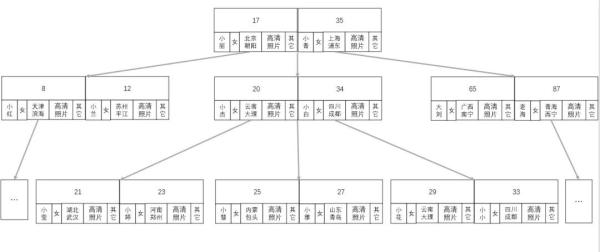
數字為用戶的年齡,其它為與樹排序查找無關的業務數據,像這種索引數據與樹排序查找無關的業務一起維護在節點的平衡多叉(階)樹稱為 B- 樹( B 樹)。
缺點:業務數據的大小可能遠遠超過了索引數據的大小,每次為了查找對比計算,需要把數據加載到內存以及 CPU 高速緩存中時,都要把索引數據和無關的業務數據全部查出來。本來一次就可以把所有索引數據加載進來,現在卻要多次才能加載完。如果所對比的節點不是所查的數據,那么這些加載進內存的業務數據就毫無用處,全部拋棄。
磁盤I/O
計算機的功能主要為:計算、存儲和網絡。而用于計算的數據以及計算后的結果很大一部分都需要存儲起來,以備后續再次使用。向磁盤中存儲和讀取的過程叫磁盤 I/O。磁盤的讀取方式和速度會嚴重影響到整個業務的計算性能。
下面我們簡單了解一下磁盤是如何工作的。
磁盤大概長這個樣子:

磁盤主要由磁盤盤片、傳動手臂、讀寫磁頭和馬達組成。
為了存儲容量,主軸像穿糖葫蘆一樣把多個磁盤片組成一個陣列。通過馬達驅動主軸轉動以及傳動手臂移動,使讀寫磁頭在磁盤片上讀寫數據。大概如下:
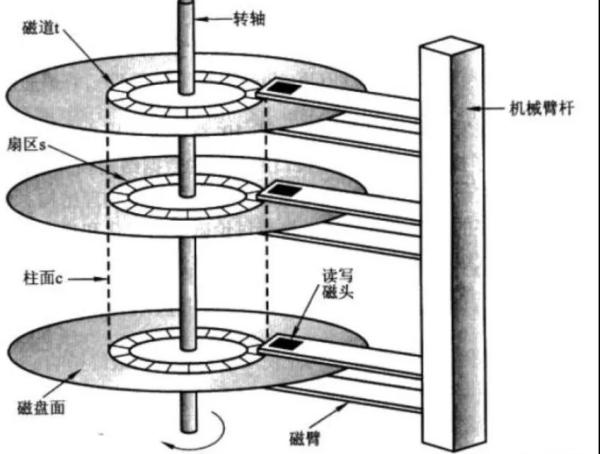
磁盤片由很多半徑不等的同心圓組成,這些圓被稱為磁道,數據就是寫在這些磁道上。

每個磁道又劃分成塊稱為扇區。
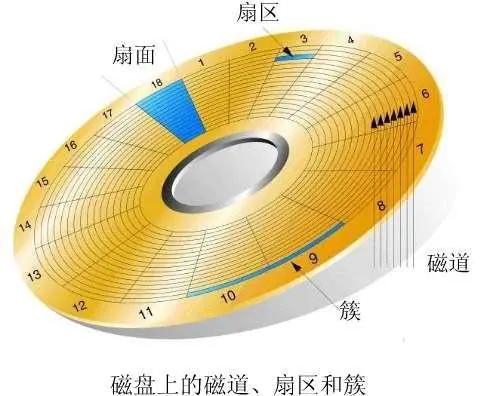
如果磁盤是一記事本,那么一張磁盤片就是本子的一頁紙,而主軸就是本子的裝訂線;磁道就是紙頁的行,而扇區可以看作是很寬的列。

如果在磁盤中存儲一首詩,想象中大概這個樣子。

磁盤的讀 I/O 操作,需要找到數據所在的磁盤片,以及對應的磁道和扇區。這些操作類似于從一本書中找到數據所在的頁,行,列。
因為每個磁盤片都對應一個磁頭,所以性能的關鍵就在于找行和列,即尋道和磁盤旋轉。尋道即通過磁頭找到數據所在的磁道,相當于換行到數據所在行。由于磁頭只能水平移動,即只能換行尋道,無法在指定磁道上移動,因此需要磁盤高速旋轉移動到指定扇區,類似寫春聯時,筆不動,紙動。
綜上所述,磁盤的讀寫是通過機械運動來定位數據所在位置,而 cpu 是通過電信號進行數字運算。粗略的認為,機械查詢數據,與光速處理數據的性能完全不是在一個量級,總之一句話就是磁盤處理太慢太慢了。
雖然磁盤處理數據太慢了,但是它是目前相對廉價且穩定的存儲設備,所以又不能舍棄不用,但大致可以通過以下方法進行優化。
盡量減少 I/O 次數,比如可以使用緩存;
每次 I/O 盡量獲取更多的數據;
每次 I/O 盡量獲取有用的數據,當然相應的也間接減少總 I/O 次數;
多叉樹之 B+tree
做為數據庫的索引,無論用什么樣的數據結構維護,這些數據最終都會存儲到磁盤中。
鑒于磁盤 I/O 的性能問題,以及每次 I/O 獲取數據量上限所限,提高索引本身 I/O 的方法最好是,減少 I/O 次數和每次獲取有用的數據。
B-tree 已經大大改進了樹家族的性能,它把多個數據集中存儲在一個節點中,本身就可能減少了 I/O 次數或者尋道次數。
但是仍然有一個致命的缺陷,那就是它的索引數據與業務綁定在一塊,而業務數據的大小很有可能遠遠超過了索引數據,這會大大減小一次 I/O 有用數據的獲取,間接的增加 I/O 次數去獲取有用的索引數據。
因為業務數據才是我們查詢最終的目的,但是它又是在「二分」查找中途過程無用的數據,因此,如果只把業務數據存儲在最終查詢到的那個節點是不是就可以了?
理想很豐滿,現實很骨瘦如柴,誰知道哪個節點就是最終要查詢的節點呢?
B+tree 橫空出世,B+ 樹就是為了拆分索引數據與業務數據的平衡多叉樹。
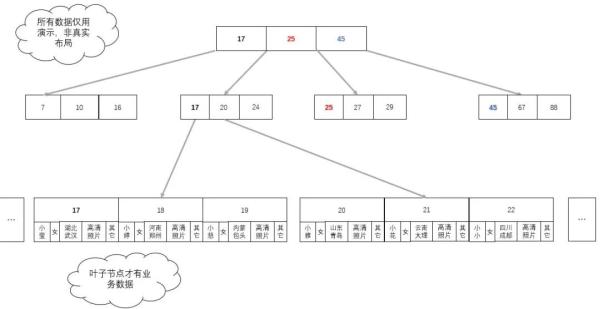
B+ 樹中,非葉子節點只保存索引數據,葉子節點保存索引數據與業務數據。這樣即保證了葉子節點的簡約干凈,數據量大大減小,又保證了最終能查到對應的業務數。既提高了單次 I/O 數據的有效性,又減少了 I/O 次數,還實現了業務。
但是,在數據中索引與數據是分離的,不像示例那樣的?
如圖:我們只需要把真實的業務數據,換成數據所在地址就可以了,此時,業務數據所在的地址在 B+ 樹中充當業務數據。
總結
數據存儲在磁盤( SSD 跟 CPU 性能也不在一個量級),而磁盤處理數據很慢;
提高磁盤性能主要通過減少 I/O 次數,以及單次 I/O 有效數據量;
索引通過多階(一個節點保存多個數據,指向多個子節點)使樹的結構更矮胖,從而減少 I/O 次數;
索引通過 B+ 樹,把業務數據與索引數據分離,來提高單次 I/O 有效數據量,從而減少 I/O 次數;
索引通過樹數據的有序和「二分查找」(多階樹可以假設為多分查找),大大縮小查詢范圍;
索引針對的是單個字段或部分字段,數據量本身比一條記錄的數據量要少的多,這樣即使通過掃描的方式查詢索引也比掃描數據庫表本身快的多;
知識擴展
樹的結構最大的優點就是查詢性能高,因此所有需要提高查詢性能的都可以考慮樹。
而現實中也確實有這樣的例子,比如:
HashMap 中的數據沖突時,鏈表轉化成紅黑樹;
數據庫索引使用的 B+ 樹;
搜索引擎倒排索引使用的字典樹;
以上只是淺嘗輒止、點到為止的描述了數據庫使用 B+ 樹索引為什么能提高查詢性能原因及簡單過程。
并沒有深入各種數據結構的細節,也未提及其它索引類型和索引的具體存儲格式,目的僅僅是,為了讓大家對索引有一個感性的認識。
到此,關于“索引能提高查詢性能的原因是什么”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。