您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“如何理解算法的復雜度”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“如何理解算法的復雜度”吧!
1. Motivation - 為什么需要復雜度分析
事后統計法(也就是把代碼運行一遍,通過統計、監控得到運行的時間和占用的內存大小)的測試結果非常依賴測試環境以及受數據規模的影響程度非常大。但是實際上更需要一個不用具體的測試數據就可以估計出算法的執行效率的方法。
2. 大 O 復雜度表示法
算法的執行效率簡單來說就是算法的執行時間。比如下面這段代碼的執行時間,假設每行代碼執行的時間是一樣的,都為 unit_time。在這個假設的基礎之上,這段代碼的總執行時間為 (2n + 2)* unit_time。
int cal(int n) { int sum = 0; int i = 1; for (;i <= n; ++i) { sum = sum + i; } return sum; }通過這個例子,可以看出總執行時間 T(n) 是與每行代碼的執行次數成正比,即可以滿足這個公式 T(n) = O(f(n)),其中 n 是數據規模的大小,f(n) 表示每行代碼執行的總次,O() 表示一個函數,即 T(n) 與 f(n) 成正比。在這個例子中 T(n) = O(2n+2),這種方式就被稱為大 O 復雜度表示法。但是實際上,大 O 時間復雜度并不具體表示代碼執行真正的執行時間,而是表示代碼執行時間隨數據規模增長的變化趨勢,也叫做漸進時間復雜度,簡稱時間復雜度。那么,在 2n+2 這個式子中,系數 2 和 常數 2 并不左右增長趨勢,比如它是線性,并不是會因為系數 2 或者常數 2 改變它線性增長的趨勢,因此又可以寫成T(n)=O(n)。又比如 T(n) = O(n^2),那么表示代碼執行時間隨數據規模 n 增長的變化趨勢是 n 平方。下面這張圖是不同時間復雜度,隨數據規模增長的執行時間變化
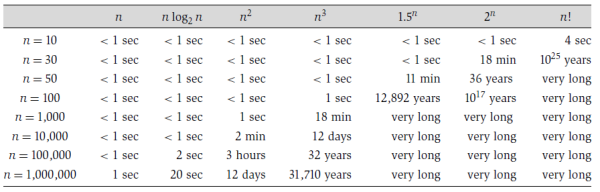
3. 時間復雜度分析
如何對一段代碼的時間復雜度進行分析呢?可以采用以下幾種方法
只關注循環次數最多的一段代碼
因為大 O 復雜度表示法只是表示一種趨勢,所以可以忽略掉公式中的常數項、低階、系數等,只記錄一個最大的量級就可以了。因此在分析一個算法、一段代碼的復雜度的時候,只需要關注循環次數最多的那一段代碼就行了。比如下面這段代碼,時間復雜度是 O(n)
int cal(int n) { int sum = 0; int i = 1; for (;i <= n; ++i) { sum = sum + i; } return sum; }加法法則:總復雜度等于量級最大的那段代碼復雜度
這個主要是省略掉大 O 復雜度中的低階項。個人感覺這個方法跟上面的方法有些重合。比如下面這段代碼中,可以按照循環分為三個段,第一個段中有個循環,但是循環次數是個常數項,對增長趨勢無任何影響,因此時間復雜度是 O(1),第二段代碼的時間復雜度是 O(n),第三個段代碼的時間復雜度是 O(n^2)。這三個段中量級最大的那個時間復雜度也就是整段代碼的時間復雜度。
int cal(int n) { int sum_1 = 0; int p = 1; for (; p < 100; ++p) { sum_1 = sum_1 + p; } int sum_2 = 0; int q = 1; for (; q < n; ++q) { sum_2 = sum_2 + q; } int sum_3 = 0; int i = 1; int j = 1; for (; i <= n; ++i) { j = 1; for (; j <= n; ++j) { sum_3 = sum_3 + i * j; } } return sum_1 + sum_2 + sum_3; }乘法法則:嵌套代碼的復雜度等于嵌套內外代碼復雜度的乘積
比如下面這段代碼中,f() 是一個循環操作,整個復雜度是 O(n),而 cal() 中的循環相當于外層,調用了 f(),假如把 f() 當成一個簡單的操作的話,那么時間復雜度是 O(n),算上 f() 真實的復雜度之后,整個 cal() 的時間復雜度是 O(n)*O(n)=O(n*n) = O(n^2)。
int cal(int n) { int ret = 0; int i = 1; for (; i < n; ++i) { ret = ret + f(i); } } int f(int n) { int sum = 0; int i = 1; for (; i < n; ++i) { sum = sum + i; } return sum; }3.1. 常見時間復雜度
| 量階 | 表示 |
|---|---|
| 常量階 | O(1) |
| 對數階 | O(logn) |
| 線性階 | O(n) |
| 線性對數階 | O(nlogn) |
| 平方階、立方階、k次方階 | O(n^2)、O(n^3)、O(n^k) |
| 指數階 | O(2^n) |
| 階乘階 | O(n!) |
| 其他階 | O(m+n)、O(m*n) |
下面針對上述的若干種時間復雜度進行闡述:
1.O(1)
O(1)是常量級時間復雜度的一種表示,只要代碼的時間不隨 n 的增大而增大,那么它的時間復雜也是 O(1)。一般情況下,只要算法中不存在循環語句、遞歸語句,即使有成千上萬行的代碼,其時間復雜度也是 O(1)。
2.O(logn)、O(nlogn)
對數時間復雜度往往比較難分析,比如下面這段代碼中
i = 1; while (i <= n) { i = i * 2; }
i = 1; while (i <= n) { i = i * 3; }
O(nlogn) 的時間復雜度就相當于上面說到的“乘法法則”:一段代碼的時間復雜度為O(logn) ,這段代碼循環 n 次,時間復雜度就是 O(nlogn) 了。
3.O(m+n)、O(m*n)
這種情況下,代碼的復雜度是由兩個數據規模決定的。如下代碼所示:
int cal(int m, int n) { int sum_1 = 0; int i = 1; for (; i < m; ++i) { sum_1 = sum_1 + i; } int sum_2 = 0; int j = 1; for (; j < n; ++j) { sum_2 = sum_2 + j; } return sum_1 + sum_2; }從這段代碼中可以看出m 和 n 是兩個數據規模,無法評估 m 和 n 的量級大小。因此,不能省略其中任何一個,所以就是 O(m+n) 了。
4.O(2^n)、O(n!)
在上述表格中列出的復雜度量級,可以粗略的分為兩類:多項式量級和非多項式量級。其中非多項式量級只有這兩個。非多項式量級的算法問題也叫做 NP(Non-Deterministic Ploynomial,非確定多項式)問題。當 n 越來越大時,非多項式量級算法的執行時間會急劇增加,求解問題的執行時間也會無限增長,所以是種很低效的算法。
3.2. 最好、最壞情況時間復雜度
比如下面這段代碼中,是在數組中查找一個數據,但是并不是把整個數組都遍歷一遍,因為有可能中途找到了就可以提前退出循環。那么,最好的情況是如果數組中第一個元素正好是要查找的變量 x ,時間復雜度就是 O(1)。最壞的情況是遍歷了整個數組都沒有找到想要的 x,那么時間復雜就成了 O(n)。因此 O(1) 就是這段代碼的最好情況時間復雜度,也就是在最好的情況下,執行這段代碼的時間復雜度。O(n) 就是這段代碼的最壞情況時間復雜度。
// n表示數組array的長度 int find(int[] array, int n, int x) { int i = 0; int pos = -1; for (; i < n; ++i) { if (array[i] == x) { pos = i; break; } } return pos; }3.3. 平均情況時間復雜度(加權平均時間復雜度或者期望時間復雜度)
最好和最壞情況時間復雜度都是極端情況發生的時間復雜度,并不常見。因此可以使用平均情況時間復雜度來表示。比如上面這段代碼中查找 x 在數組中的位置有兩種情況,一種是在數組中,另一種是不在數組中。在數組中又可以在數組中的 0~n-1 位置。假設在數組中和不在數組中的概率分別為 1/2,在數組中的 0~n-1 的位置概率都一樣,為 1/(2 *n)。因此,上述這段的平均情況時間復雜度(或者叫加權平均時間復雜度、期望時間復雜度)為
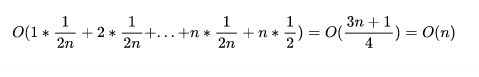
假如使用如下公式計算復雜度的話,那么就相當于每種情況的發生概率都是 1/(n+1) 了,沒有考慮每種的情況的不同概率,存在一定不準確性。
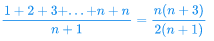
3.4. 均攤時間復雜度
均攤時間復雜度采用的是攤還分析法(平攤分析法)。就是把耗時多的操作,平攤到其他那些時間復雜度比較低的操作上。比如下面這段代碼
// array表示一個長度為n的數組 // 代碼中的array.length就等于n int[] array = new int[n]; int count = 0; void insert(int val) { if (count == array.length) { int sum = 0; for (int i = 0; i < array.length; ++i) { sum = sum + array[i]; } array[0] = sum; count = 1; } array[count] = val; ++count; }這段代碼想要實現的就是往一個數組中插入數據,如果數組滿了的話,那么就求和之后的 sum 放到數組的第一個位置,之后繼續將數據插入到數組中。通過分析可以發現,這段代碼的最好情況時間復雜度是 O(1),最壞情況時間復雜度是 O(n),平均時間復雜度是 O(1)。
那么這段代碼中,在大部分情況下,時間復雜度是 O(1),只有個別情況下,復雜度才是 O(n)。并且,O(1) 和 O(n) 出現的比較規律,一般一個 O(n) 執行之后,會出現 n-1 個 O(1) 的執行。針對這種情況,可以使用攤還分析法,就是把 O(n) 這個耗時多的時間復雜度均攤到接下來的 n-1 個 O(1) 的執行上,均攤下來的時間復雜度為 O(1),這個時間復雜度就是均攤時間復雜度。
那么均攤時間復雜度不怎么常見,常見的場景是:對一個數據結構進行一組連續操作,大部分情況下時間復雜度都很低,只有個別情況下時間復雜度比較高。而且這些操作之間存在前后連貫的時序關系,比如上面提到的先是一系列 O(1) 的時間復雜度操作,接下來是 O(n) 的時間復雜度操作。這個時候就可以采用攤還分析法將較高時間復雜度的那次操作的耗時平攤到其他時間復雜度比較低的操作上。
一般均攤時間復雜度等于最好情況時間復雜度。那么如何區別平均時間復雜度和均攤時間復雜度呢?我覺得看你使用哪種方法,假如使用攤還分析法算出來的時間復雜度就是均攤時間復雜度,使用加權方式、或者期望值計算方式算出來的時間復雜度就是平均時間復雜度。
4. 空間復雜度分析
空間復雜度分析方法很簡單。時間復雜度的全稱叫做漸進時間復雜度,表示算法的執行時間與數據規模之間的增長關系。那么空間復雜度全稱叫做漸進空間復雜度,表示算法的存儲空間與數據規模之間的增長關系。
比如下面這段代碼中,首先 int i= 0; 申請一個空間存儲變量,是常量可以忽略,int[] a = new int[n]; 申請了一個大小為 n 的 int 類型數組,剩下的代碼都沒有占用更多的空間,因此空間復雜度是 O(n)
void print(int n) { int i = 0; int[] a = new int[n]; for (i; i <n; ++i) { a[i] = i * i; } for (i = n-1; i >= 0; --i) { print out a[i] } }對于空間復雜度分析,其實比較簡單,一般看變量聲明時分配的空間大小即可。
4.1. 常用時間復雜度
| 量階 | 表示 |
|---|---|
| 常數階 | O(1) |
| 線性階 | O(n) |
| 平方階 | O(n^2) |
常用的空間復雜度就上面 3 種,O(nlogn)、O(logn)這樣的對數階復雜度一般都用不到。
5. 總結
回顧一下復雜度分析,總的來說時間復雜度的 motivation 是我們想要一個不用具體數據就可以估算出算法的執行效率的方法。而時間復雜度采用的是大 O 表示法,大 O 表示法其實描述的是一個增長趨勢。比如 n^2 中,當 n 的值越來越大時候,O(n^2) 這個算法的執行時間是成平方增長的,而 O(n) 這個算法的執行時間是成直線型增長的,因此 O(n^2) 的時間復雜度是更高(見第一張圖)。之后是幾種常用的時間復雜度,平均時間復雜度、最好最壞時間復雜度,均攤時間復雜度(均攤這種思想在操作系統中有一定的體現:RR 調度算法中,在時間片大小選擇上,有著類似的處理方式,因為 RR 是一個搶占式調度算法,當發生調度之后會發生進程的上下文切換,而進程的上下文切換是需要額外的時間成本,而這個時間成本會均攤到時間片上,當時間片很大時,顯然均攤的效果不錯,因此這個額外的時間成本影響會很小)
為什么說掌握時間復雜度是掌握了根本大法?去年上課的時候,記憶比較深刻的是老師好像在講一個比較難的算法問題,然后從最簡單、復雜度最高的解法開始講起,然后跟帶著我們一步一步分析每一塊代碼的時間復雜度,然后說這塊的代碼的時間復雜度是 O(n^2),我們能不能想辦法把它給降下來的呢?然后就在那思考了怎么降了,一句一句代碼看過去,畫圖等等,最終將時間復雜度降下來了。因此個人覺得掌握時間復雜度分析之后,掌握的是算法的分析方法,你可以分析出每段代碼的復雜度,然后通過思考最終把相應代碼的時間復雜度降下來。假如你復雜度分析掌握不熟,那么怎么降都不知道,那么算法的優化也就沒了。
到此,相信大家對“如何理解算法的復雜度”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。