您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“如何理解布隆過濾器算法的實現原理”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“如何理解布隆過濾器算法的實現原理”吧!
布隆過濾器的一些概念主要包括:
簡介
算法
參數
優勢和劣勢
布隆過濾器簡介
布隆過濾器是「一種空間高效概率性的數據結構」(百科中原文是a space-efficient probabilistic data structure),該數據結構于1970年由Burton Howard Bloom提出,「作用是測試一個元素是否某個集合的一個成員」。布隆過濾器是可能出現false positive(這個是專有名詞"假陽性",可以理解為誤判的情況,下文如果用到這個名詞會保留英文單詞使用)匹配的,換言之,布隆過濾器在使用的時候有可能返回結果"可能存在于集合中"或者"必定不存在于集合中"。
布隆過濾器算法描述
在場景復雜的網絡爬蟲中,爬取到的網頁URL依賴有可能成環,例如在URL-1頁面中展示了URL-2,然后又在URL-2中的頁面展示了URL-1,這個時候需要一種方案記錄和判斷歷史訪問過的URL。這個時候可能會想到下面的方案:
方案二:使用HashSet(其實這里不局限于HashSet,鏈表、樹和散列表等數據結構都能滿足)存儲已經訪問過的URL
方案三:基于方案一和方案二進行優化,存儲URL的摘要,使用摘要算法如MD5、SHA-n算法針對URL字符串生成摘要
方案四:使用Hash函數處理對應的URL生成一個哈希碼,再把哈希碼通過一個映射函數映射到一個固定容量的BitSet中的某一個比特
對于方案一、方案二和方案三,在歷史訪問URL數據量極大的情況下,會消耗巨大的存儲空間(磁盤或者內存),對于方案四,如果URL有100億個,那么要把沖突幾率降低到1%,那么BitSet的容量需要設置為10000億。
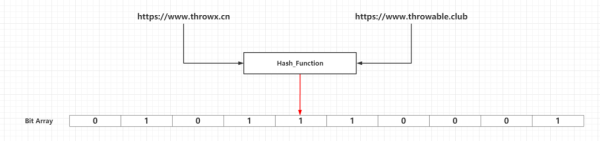
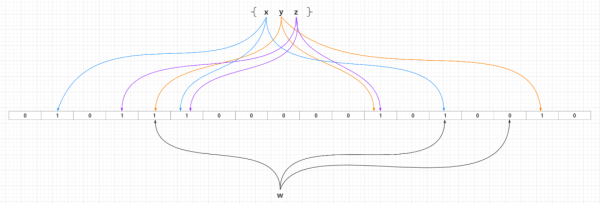
所以上面的四種方案都有明顯的不足之處,而布隆過濾器算法的基本思路跟方案四差不多,最大的不同點就是方案四中只提到使用了一個散列函數,而布隆過濾器中使用了k(k >= 1)個相互獨立的高效低沖突的散列函數。
一個初始化的布隆過濾器是一個所有比特都設置為0的長度為m的比特數組,也就是認知中的Bit Array、Bit Set或者Redis中的Bit Map概念。然后需要引入k個不同的散列函數,某個新增元素通過這k個散列函數處理之后,映射到比特數組m個比特中的k個,并且把這些命中映射的k個比特位設置為1,產生一個均勻的隨機分布。通常情況下,k的一個較小的常數,取決于所需的誤判率,而布隆過濾器容量m與散列函數個數k和需要添加元素數量呈正相關。
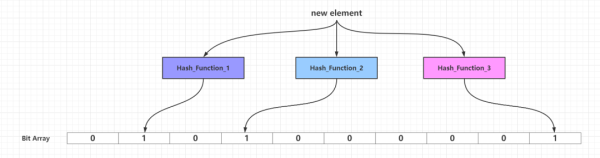
當需要新增的所有元素都添加到布隆過濾器之后,那么比特數組中的很多比特都被設置為1。這個時候如果需要判斷一個元素是否存在于布隆過濾器中,只需要通過k個散列函數處理得到比特數組的k個下標,然后判斷比特數組對應的下標所在比特是否為1。如果這k個下標所在比特中「至少存在一個0,那么這個需要判斷的元素必定不在布隆過濾器代表的集合中」;如果這k個下標所在比特全部都為1,那么那么這個需要判斷的元素「可能存在于」布隆過濾器代表的集合中或者剛好是一個False Positive,至于誤差率分析見下文的「布隆過濾器的相關參數」一節。False Positive出現的情況可以見下圖:
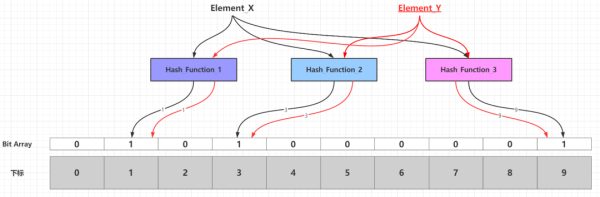
當添加到布隆過濾器的元素數量比較大,并且布隆過濾器的容量設置不合理(過小),容易出現多個元素通過k個散列函數,映射到相同的k個位(如上圖的下標1、3、9所在的位),這個時候就無法準確判斷這k個位由具體那個元素映射而來。其實可以極端一點思考:假設布隆過濾器容量為24,散列函數只有一個,那么添加最多25個不同元素,必定有兩個不同的元素的映射結果落在同一個位。
布隆過濾器的相關參數
在算法描述一節已經提到過,布隆過濾器主要有下面的參數:
初始化比特數組容量m
散列函數個數k
誤判率ε(數學符號Epsilon,代表False Positive Rate)
需要添加到布隆過濾器的元素數量n
考慮到篇幅原因,這里不做這幾個值的關系推導,直接整理出結果和關系式。
誤判率ε的估算值為:[1 - e^(-kn/m)]^k
最優散列函數數量k的推算值:對于給定的m和n,當k = m/n * ln2的時候,誤判率ε最低
推算初始化比特容量m的值,當k = m/n * ln2的時候,m >= n * log2(e) * log2(1/ε)
這里貼一個參考資料中m/n、k和False Positive Rate之間的關系圖:
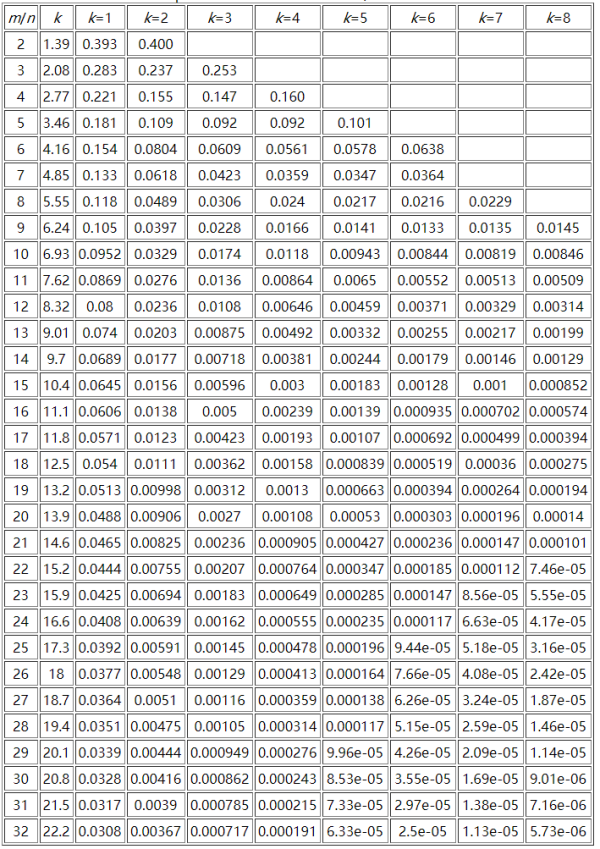
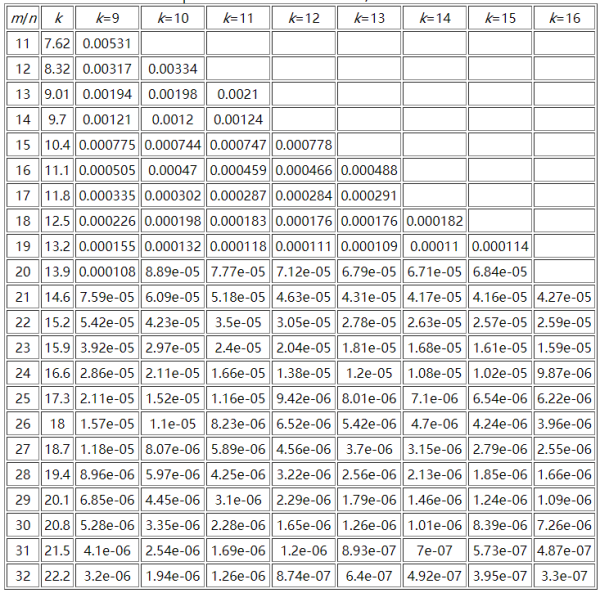
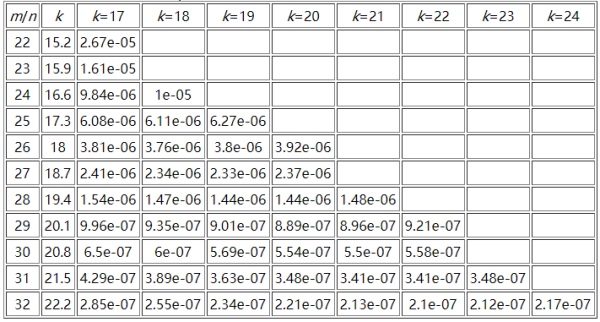
這里可以推算一下表格中最大參數所需要的空間極限,假設n為10億,m/n = 32,那么m為320億,而k為24,此時的誤判率為2.17e-07(0.000000217),需要空間3814.69727m。一般規律是:
當k固定的時候,m/n越大,誤判率越小
當m/n固定的時候,k越大,誤判率越大
通常情況下,k需要固定,而n是無法確定準確值,最好要評估增長趨勢預先計算一個比較大的m值去降低誤判率,當然也要權衡m值過大導致空間消耗過大的問題。
既然參數的關系式都已經有推導結果,可以基于關系式寫一個參數生成器:
import java.math.BigDecimal; import java.math.RoundingMode; public class BloomFilterParamGenerator { public BigDecimal falsePositiveRate(int m, int n, int k) { double temp = Math.pow(1 - Math.exp(Math.floorDiv(-k * n, m)), k); return BigDecimal.valueOf(temp).setScale(10, RoundingMode.FLOOR); } public BigDecimal kForMinFalsePositiveRate(int m, int n) { BigDecimal k = BigDecimal.valueOf(Math.floorDiv(m, n) * Math.log(2)); return k.setScale(10, RoundingMode.FLOOR); } public BigDecimal bestM(int n, double falsePositiveRate) { double temp = log2(Math.exp(1) + Math.floor(1 / falsePositiveRate)); return BigDecimal.valueOf(n).multiply(BigDecimal.valueOf(temp)).setScale(10, RoundingMode.FLOOR); } public double log2(double x) { return Math.log(x) / Math.log(2); } public static void main(String[] args) { BloomFilterParamGenerator generator = new BloomFilterParamGenerator(); System.out.println(generator.falsePositiveRate(2, 1, 2)); // 0.3995764008 System.out.println(generator.kForMinFalsePositiveRate(32, 1)); // 22.1807097779 System.out.println(generator.bestM(1, 0.3995764009)); // 2.2382615950 } }這里的計算沒有考慮嚴格的進位和截斷,所以和實際的結果可能有偏差,只提供一個參考的例子。
布隆過濾器的優勢和劣勢
布隆過濾器的優勢:
布隆過濾器相對于其他數據結構在時空上有巨大優勢,占用內存少,查詢和插入元素的時間復雜度都是O(k)
可以準確判斷元素不存在于布隆過濾器中的場景
散列函數可以獨立設計
布隆過濾器不需要存儲元素本身,適用于某些數據敏感和數據嚴格保密的場景
布隆過濾器的劣勢:
不能準確判斷元素必定存在于布隆過濾器中的場景,存在誤判率,在k和m固定的情況下,添加的元素越多,誤判率越高
沒有存儲全量的元素,對于一些準確查詢或者準確統計的場景不適用
原生的布隆過濾器無法安全地刪除元素
這里留一個很簡單的問題給讀者:為什么原生的布隆過濾器無法安全地刪除元素?(可以翻看之前的False Positive介紹)
布隆過濾器算法實現
著名的Java工具類庫Guava中自帶了一個beta版本的布隆過濾器實現,這里參考其中的源碼實現思路和上文中的算法描述進行一次布隆過濾器的實現。先考慮設計散列函數,簡單一點的方式就是參考JavaBean的hashCode()方法的設計:
// 下面的方法來源于java.util.Arrays#hashCode public static int hashCode(Object a[]) { if (a == null) return 0; int result = 1; for (Object element : a) result = 31 * result + (element == null ? 0 : element.hashCode()); return result; }上面方法的31可以作為一個輸入的seed,每個散列函數設計一個獨立的seed,并且這個seed值選用素數基于字符串中的每個char進行迭加就能實現計算出來的結果是相對獨立的:
import java.util.Objects; public class HashFunction { /** * 布隆過濾器容量 */ private final int m; /** * 種子 */ private final int seed; public HashFunction(int m, int seed) { this.m = m; this.seed = seed; } public int hash(String element) { if (Objects.isNull(element)) { return 0; } int result = 1; int len = element.length(); for (int i = 0; i < len; i++) { result = seed * result + element.charAt(i); } // 這里確保計算出來的結果不會超過m return (m - 1) & result; } }接著實現布隆過濾器:
public class BloomFilter { private static final int[] K_SEED_ARRAY = {5, 7, 11, 13, 31, 37, 61, 67}; private static final int MAX_K = K_SEED_ARRAY.length; private final int m; private final int k; private final BitSet bitSet; private final HashFunction[] hashFunctions; public BloomFilter(int m, int k) { this.k = k; if (k <= 0 && k > MAX_K) { throw new IllegalArgumentException("k = " + k); } this.m = m; this.bitSet = new BitSet(m); hashFunctions = new HashFunction[k]; for (int i = 0; i < k; i++) { hashFunctions[i] = new HashFunction(m, K_SEED_ARRAY[i]); } } public void addElement(String element) { for (HashFunction hashFunction : hashFunctions) { bitSet.set(hashFunction.hash(element), true); } } public boolean contains(String element) { if (Objects.isNull(element)) { return false; } boolean result = true; for (HashFunction hashFunction : hashFunctions) { result = result && bitSet.get(hashFunction.hash(element)); } return result; } public int m() { return m; } public int k() { return k; } public static void main(String[] args) { BloomFilter bf = new BloomFilter(24, 3); bf.addElement("throwable"); bf.addElement("throwx"); System.out.println(bf.contains("throwable")); // true } }這里的散列算法和有限的k值不足以應對復雜的場景,僅僅為了說明如何實現布隆過濾器,總的來說,原生布隆過濾器算法是比較簡單的。對于一些復雜的生產場景,可以使用一些現成的類庫如Guava中的布隆過濾器API、Redis中的布隆過濾器插件或者Redisson(Redis高級客戶端)中的布隆過濾器API。
布隆過濾器應用
主要包括:
Guava中的API
Redisson中的API
使用場景
使用Guava中的布隆過濾器API
引入Guava的依賴:
<dependency> <groupId>com.google.guava</groupId> <artifactId>guava</artifactId> <version>30.1-jre</version> </dependency>
使用布隆過濾器:
import com.google.common.hash.BloomFilter; import com.google.common.hash.Funnels; import java.nio.charset.StandardCharsets; public class GuavaBloomFilter { @SuppressWarnings("UnstableApiUsage") public static void main(String[] args) { BloomFilter<CharSequence> bloomFilter = BloomFilter.create(Funnels.stringFunnel(StandardCharsets.US_ASCII), 10000, 0.0444D); bloomFilter.put("throwable"); bloomFilter.put("throwx"); System.out.println(bloomFilter.mightContain("throwable")); System.out.println(bloomFilter.mightContain("throwx")); } }構造BloomFilter的最多參數的靜態工廠方法是BloomFilter
funnel:主要是把任意類型的數據轉化成HashCode,是一個頂層接口,有大量內置實現,見Funnels
expectedInsertions:期望插入的元素個數
fpp:猜測是False Positive Percent,誤判率,小數而非百分數,默認值0.03
strategy:映射策略,目前只有MURMUR128_MITZ_32和MURMUR128_MITZ_64(默認策略)
參數可以參照上面的表格或者參數生成器的指導,基于實際場景進行定制。
使用Redisson中的布隆過濾器API
高級Redis客戶端Redisson已經基于Redis的bitmap數據結構做了封裝,屏蔽了復雜的實現邏輯,可以開箱即用。引入Redisson的依賴:
<dependency> <groupId>org.redisson</groupId> <artifactId>redisson</artifactId> <version>3.15.1</version> </dependency>
使用Redisson中的布隆過濾器API:
import org.redisson.Redisson; import org.redisson.api.RBloomFilter; import org.redisson.api.RedissonClient; import org.redisson.config.Config; public class RedissonBloomFilter { public static void main(String[] args) { Config config = new Config(); config.useSingleServer() .setAddress("redis://127.0.0.1:6379"); RedissonClient redissonClient = Redisson.create(config); RBloomFilter<String> bloomFilter = redissonClient.getBloomFilter("ipBlockList"); // 第一個參數expectedInsertions代表期望插入的元素個數,第二個參數falseProbability代表期望的誤判率,小數表示 bloomFilter.tryInit(100000L, 0.03D); bloomFilter.add("127.0.0.1"); bloomFilter.add("192.168.1.1"); System.out.println(bloomFilter.contains("192.168.1.1")); // true System.out.println(bloomFilter.contains("192.168.1.2")); // false } }Redisson提供的布隆過濾器接口RBloomFilter很簡單:

常用的方法有tryInit()(初始化)、add()(添加元素)和contains()(判斷元素是否存在)。相對于Guava的內存態的布隆過濾器實現,Redisson提供了基于Redis實現的「分布式布隆過濾器」,可以滿足分布式集群中布隆過濾器的使用。
布隆過濾器使用場景
其實布隆過濾器的使用場景可以用百科中的一張示意圖來描述:
基于上圖具體化的一些場景列舉如下:
網站爬蟲應用中進行URL去重(不存在于布隆過濾器中的URL必定是未爬取過的URL)
防火墻應用中IP黑名單判斷(不局限于IP黑名單,通用的黑名單判斷場景基本都可以使用布隆過濾器,不存在于布隆過濾器中的IP必定是白名單)
用于規避緩存穿透(不存在于布隆過濾器中的KEY必定不存在于后置的緩存中)
布隆過濾器變體
布隆過濾器的變體十分多,主要是為了解決布隆過濾器算法中的一些缺陷或者劣勢。常見的變體如下:
| 變體名稱 | 變體描述 |
|---|---|
Counting Bloom Filter | 把原生布隆過濾器每個位替換成一個小的計數器(Counter),所謂計數器其實就是一個小的整數 |
Compressed Bloom Filter | 對位數組進行壓縮 |
Hierarchical Bloom Filters | 分層,由多層布隆過濾器組成 |
Spectral Bloom Filters | CBF的擴展,提供查詢集合元素的出現頻率功能 |
Bloomier Filters | 存儲函數值,不僅僅是做位映射 |
Time-Decaying Bloom Filters | 計數器數組替換位向量,優化每個計數器存儲其值所需的最小空間 |
Space Code Bloom Filter | - |
Filter Banks | - |
Scalable Bloom filters | - |
Split Bloom Filters | - |
Retouched Bloom filters | - |
Generalized Bloom Filters | - |
Distance-sensitive Bloom filters | - |
Data Popularity Conscious Bloom Filters | - |
Memory-optimized Bloom Filter | - |
Weighted Bloom filter | - |
Secure Bloom filters | - |
這里挑選Counting Bloom Filter(簡稱CBF)變體稍微展開一下。原生布隆過濾器的基礎數據結構是位向量,CBF擴展原生布隆過濾器的基礎數據結構,底層數組的每個元素使用4位大小的計數器存儲添加元素到數組某個下標時候映射成功的頻次,在插入新元素的時候,通過k個散列函數映射到k個具體計數器,這些命中的計數器值增加1;刪除元素的時候,通過k個散列函數映射到k個具體計數器,這些計數器值減少1。使用CBF判斷元素是否在集合中的時候:
某個元素通過k個散列函數映射到k個具體計數器,所有計數器的值都為0,那么元素必定不在集合中
某個元素通過k個散列函數映射到k個具體計數器,至少有1個計數器的值大于0,那么元素可能在集合

小結一句話簡單概括布隆過濾器的基本功能:「不存在則必不存在,存在則不一定存在。」
在使用布隆過濾器判斷一個元素是否屬于某個集合時,會有一定的誤判率。也就是有可能把不屬于某個集合的元素誤判為屬于這個集合,這種錯誤稱為False Positive,但不會把屬于某個集合的元素誤判為不屬于這個集合(相對于False Positive,"假陽性",如果屬于某個集合的元素誤判為不屬于這個集合的情況稱為False Negative,"假陰性")。False Positive,也就是錯誤率或者誤判率這個因素的引入,是布隆過濾器在設計上權衡空間效率的關鍵。
感謝各位的閱讀,以上就是“如何理解布隆過濾器算法的實現原理”的內容了,經過本文的學習后,相信大家對如何理解布隆過濾器算法的實現原理這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。