您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關softmax函數用法及案例分析,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
如下所示:
def softmax(logits, axis=None, name=None, dim=None):
"""Computes softmax activations.
This function performs the equivalent of
softmax = tf.exp(logits) / tf.reduce_sum(tf.exp(logits), axis)
Args:
logits: A non-empty `Tensor`. Must be one of the following types: `half`,
`float32`, `float64`.
axis: The dimension softmax would be performed on. The default is -1 which
indicates the last dimension.
name: A name for the operation (optional).
dim: Deprecated alias for `axis`.
Returns:
A `Tensor`. Has the same type and shape as `logits`.
Raises:
InvalidArgumentError: if `logits` is empty or `axis` is beyond the last
dimension of `logits`.
"""
axis = deprecation.deprecated_argument_lookup("axis", axis, "dim", dim)
if axis is None:
axis = -1
return _softmax(logits, gen_nn_ops.softmax, axis, name)softmax函數的返回結果和輸入的tensor有相同的shape,既然沒有改變tensor的形狀,那么softmax究竟對tensor做了什么?
答案就是softmax會以某一個軸的下標為索引,對這一軸上其他維度的值進行 激活 + 歸一化處理。
一般來說,這個索引軸都是表示類別的那個維度(tf.nn.softmax中默認為axis=-1,也就是最后一個維度)
舉例:
def softmax(X, theta = 1.0, axis = None): """ Compute the softmax of each element along an axis of X. Parameters ---------- X: ND-Array. Probably should be floats. theta (optional): float parameter, used as a multiplier prior to exponentiation. Default = 1.0 axis (optional): axis to compute values along. Default is the first non-singleton axis. Returns an array the same size as X. The result will sum to 1 along the specified axis. """ # make X at least 2d y = np.atleast_2d(X) # find axis if axis is None: axis = next(j[0] for j in enumerate(y.shape) if j[1] > 1) # multiply y against the theta parameter, y = y * float(theta) # subtract the max for numerical stability y = y - np.expand_dims(np.max(y, axis = axis), axis) # exponentiate y y = np.exp(y) # take the sum along the specified axis ax_sum = np.expand_dims(np.sum(y, axis = axis), axis) # finally: divide elementwise p = y / ax_sum # flatten if X was 1D if len(X.shape) == 1: p = p.flatten() return p c = np.random.randn(2,3) print(c) # 假設第0維是類別,一共有里兩種類別 cc = softmax(c,axis=0) # 假設最后一維是類別,一共有3種類別 ccc = softmax(c,axis=-1) print(cc) print(ccc)
結果:
c: [[-1.30022268 0.59127472 1.21384177] [ 0.1981082 -0.83686108 -1.54785864]] cc: [[0.1826746 0.80661068 0.94057075] [0.8173254 0.19338932 0.05942925]] ccc: [[0.0500392 0.33172426 0.61823654] [0.65371718 0.23222472 0.1140581 ]]
可以看到,對axis=0的軸做softmax時,輸出結果在axis=0軸上和為1(eg: 0.1826746+0.8173254),同理在axis=1軸上做的話結果的axis=1軸和也為1(eg: 0.0500392+0.33172426+0.61823654)。
這些值是怎么得到的呢?
以cc為例(沿著axis=0做softmax):

以ccc為例(沿著axis=1做softmax):
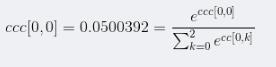
知道了計算方法,現在我們再來討論一下這些值的實際意義:
cc[0,0]實際上表示這樣一種概率: P( label = 0 | value = [-1.30022268 0.1981082] = c[*,0] ) = 0.1826746
cc[1,0]實際上表示這樣一種概率: P( label = 1 | value = [-1.30022268 0.1981082] = c[*,0] ) = 0.8173254
ccc[0,0]實際上表示這樣一種概率: P( label = 0 | value = [-1.30022268 0.59127472 1.21384177] = c[0]) = 0.0500392
ccc[0,1]實際上表示這樣一種概率: P( label = 1 | value = [-1.30022268 0.59127472 1.21384177] = c[0]) = 0.33172426
ccc[0,2]實際上表示這樣一種概率: P( label = 2 | value = [-1.30022268 0.59127472 1.21384177] = c[0]) = 0.61823654
將他們擴展到更多維的情況:假設c是一個[batch_size , timesteps, categories]的三維tensor
output = tf.nn.softmax(c,axis=-1)
那么 output[1, 2, 3] 則表示 P(label =3 | value = c[1,2] )
關于softmax函數用法及案例分析就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。