您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關用Python實習唯美星空的方法,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
用Python顯示真實的星空
還是先上圖
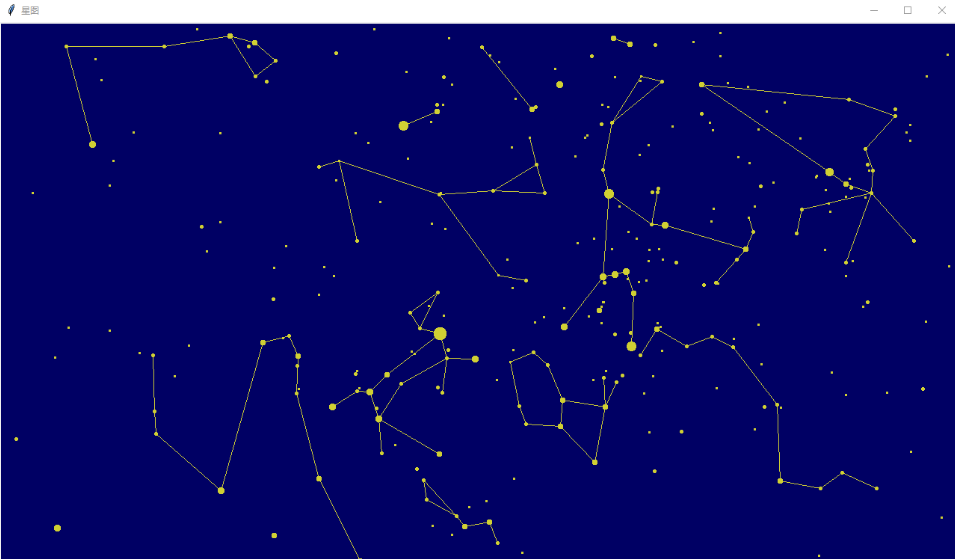 本文講怎樣畫出真實的星空。
本文講怎樣畫出真實的星空。
預備知識
如果想顯示真實的星空,首先你得有真實恒星的位置坐標和亮度標記。它的基本格式如下:
{'long': 0.023278328898474372, 'lat': -0.09961466705757636, 'light': 46, 'const': 66},
{'long': 0.024870941840919196, 'lat': 0.2338062439126301, 'light': 55, 'const': 62},
{'long': 0.028107061526797, 'lat': 1.1204335039257496, 'light': 56, 'const': 18},
{'long': 0.03660100303760025, 'lat': 0.5077259659824991, 'light': 21, 'const': 1},
{'long': 0.04004802831028905, 'lat': 1.0323574005393255, 'light': 23, 'const': 18},
{'long': 0.03944444109507185, 'lat': 0.3178583859888262, 'light': 55, 'const': 62},
{'long': 0.040797071265367454, 'lat': -0.488478858963941, 'light': 54, 'const': 74},
{'long': 0.0410661312228549, 'lat': -0.798444499556106, 'light': 39, 'const': 64},
{'long': 0.043800486202076855, 'lat': 0.1945266317121166, 'light': 55, 'const': 66},
{'long': 0.045036755271142, 'lat': 0.804111967609767, 'light': 50, 'const': 1},
{'long': 0.043785947609407745, 'lat': -1.4350775693910554, 'light': 53, 'const': 58},
{'long': 0.04915283505929031, 'lat': -0.2699684886295715, 'light': 49, 'const': 21},
{'long': 0.050498187206605094, 'lat': -0.4851966800391031, 'light': 54, 'const': 74},每顆星星包含4個信息:天球經度long、天球緯度lat、亮度light(越小越亮)、所屬星座const。
想象所有的星星都鑲嵌在一個天球上,它們的位置是固定不變的,所以叫做恒星。
星星的坐標用經緯度來表示,就如同地球上的位置用經緯度來表示。當地球旋轉時,我們看到的是天球的旋轉。
我們所熟悉的北極星,就在非常靠近天球北極的位置上。
在天球旋轉的過程中,它的位置幾乎不動。也就是說北極星的位置幾乎在任何時候都保持在天空中固定的位置上。之所以能夠用北極星來指示方向,也就是這個原理。
另外,星空是球形的,想把它顯示在屏幕上,又涉及幾組基本參數的設置:
觀測地的經緯度
觀測的日期和時間
觀測者的觀測角度和屏幕大小
這幾組參數中,關系是這樣的:觀測地的維度是第一位的,觀測地確定后,所能看到的星空就是確定的(天球傾角),只有在赤道上能夠看到所有的星星,在其它維度都會有一些星星看不到。
最極端的情況下是在兩極地區,永遠只能看到半個天球(即一半數量的星星)。
觀測地的經度、觀測日期和觀測時間這三者其實是等價的,因為地球的公轉和自轉對于遙遠的星空來說,可以認為沒有差別。
當觀測點和觀測日期時間都確定后,理論可以認為所能看到的星空大約有全天中半數的星星。但能夠顯示在屏幕上的星星,則取決于你向哪里觀看以及屏幕有多大。
如果能夠理解上面這些基本知識,請繼續往下看。
星空計算
計算經過這樣幾個步驟:
1、為了便于計算,首先將每顆星星的經緯度轉換為xyz的三維坐標。在這種轉換過程中,我們看到的是正立的天球,北極點向上,南極點在下。
2、將觀測地的緯度引入每顆計算
3、將觀測地經度、觀測日期、觀測時間三者結合起來,形成一個經度數據,引入每顆計算
4、將觀測者的朝向引入每顆計算
5、將觀測者的仰角引入每顆計算
6、向屏幕投影
代碼如下:
def calcStar(stars,Long,Lat,winLong,winLat,eyeDistant): Long= radians(Long) Lat= radians(Lat) winLong= radians(winLong) winLat= radians(winLat) for star in stars: # print(star) # 經緯度轉換為xyz的三維坐標 x0= cos(star['long'])* cos(star['lat']) y0= sin(star['long'])* cos(star['lat']) z0= sin(star['lat']) # 觀測地經度及日期時間的合并 x1= x0*cos(Long)- y0*sin(Long) y1= x0*sin(Long)+ y0*cos(Long) z1= z0 # 觀測地緯度 x2= x1* sin(Lat)- z1* cos(Lat) y2= y1; z2= x1* cos(Lat)+ z1* sin(Lat) # 觀測者轉身 x3= x2* cos(winLong)+ y2* sin(winLong) y3= -x2* sin(winLong)+ y2* cos(winLong) z3= z2 # 觀測者俯仰 x4= x3* sin(winLat)- z3* cos(winLat) y4= y3 z4= x3* cos(winLat)+ z3* sin(winLat) # 屏幕投影 star['visible']= (z2> 0 and z4>0) star['x']= x4* eyeDistant/z4 star['y']= y4* eyeDistant/z4 star['z']= z4
星星可見的條件是:在地平線之上(z2>0)并且在觀測者面前(z4>0),而可見的星星是否真正顯示在屏幕上的則取決于它是否在屏幕顯示范圍內。
顯示代碼如下:
img= Image.new('RGBA', (1280,720), (0,0,120,255)) # 深藍色天空
draw = ImageDraw.Draw(img)
color= (255,255,0,255) # 黃色星星
for star in stars:
# 屏幕中心
x= round(-star['y']+ 640)
y= round(star['x']+ 360)
# 亮度值越小越亮,這里用大小來表示
r= round(6-star['light']/10)
if visible(star):
# print(x,y)
draw.ellipse((x-r, y-r, x+r, y+r), fill=color)
img.show()怎樣將經度、觀測日期和觀測時間結合起來
這個問題比想象的復雜太多。如果想做到真正的精確,會涉及平太陽日、真太陽日、恒星日、歲差、經度與本地時間的差異,等等很多細節。
不過,好在這些誤差并不太大,如果你的目標不是科研,并且只考慮近代而不是遠古和未來,有些誤差即使忽略也沒有太大的影響。
這里我用一個雖然簡略,但足夠精確的一個經驗公式來計算。輸入觀測地經度、觀測日期和時間,返回一個所謂的絕對經度,以這個經度作為我們計算星空位置所使用的經度值。
代碼如下:
def getAbsLong(aLong, ayy, amm, add, ahh, amin): # 年的影響忽略 # 月日的影響,首先計算太陽赤經 # 春分點3月21日為經度0,一年平均365.25天,旋轉360度,用插值方法簡單計算 a= julianDay(ayy, amm, add) b= julianDay(ayy, 3, 21) v= 0- (a-b)/365.25*360 # 因為使用本地時間,基本可以忽略經度+時區的影響(互相抵消) # 時分的影響,中午12點,正對太陽赤經,一天24小時,旋轉360度,用插值簡單計算 c= ahh*60+amin d= 12*60 v= v- (c-d)/(24*60)*360 return v
星座連線是怎么來的
星座連線用于輔助我們理解星座形狀。結構很簡單,就是指明一條線關聯哪兩個點。這里不展開了,詳見代碼。
{'star1': 61, 'star2': 4, 'const': 1},
{'star1': 60, 'star2': 61, 'const': 1},
{'star1': 83, 'star2': 60, 'const': 1},
{'star1': 83, 'star2': 109, 'const': 1},
{'star1': 61, 'star2': 58, 'const': 1},
{'star1': 58, 'star2': 22, 'const': 1},
{'star1': 22, 'star2': 3097, 'const': 1},
{'star1': 3097, 'star2': 3097, 'const': 1},
{'star1': 3097, 'star2': 3088, 'const': 1},
{'star1': 3007, 'star2': 3090, 'const': 1},
{'star1': 142, 'star2': 61, 'const': 1},關于用Python實習唯美星空的方法就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。