您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文實例講述了Java貪心算法之Prime算法原理與實現方法。分享給大家供大家參考,具體如下:
Prime算法:是一種窮舉查找算法來從一個連通圖中構造一棵最小生成樹。利用始終找到與當前樹中節點權重最小的邊,找到節點,加到最小生成樹的節點集合中,直至所有節點都包括其中,這樣就構成了一棵最小生成樹。prime在算法中屬于貪心算法的一種,貪心算法還有:Kruskal、Dijkstra以及哈夫曼樹及編碼算法。
下面具體講一下prime算法:
1、首先需要構造一顆最小生成樹,以及兩個節點之間的權重數組,在此我們用一個二維數組來代表這樣一個連通圖的形式。節點就是0~數組長度-1,10000代表節點本身,權重 >= 100代表兩個節點不連通,反之連通。
構建連通圖代碼如下:
// 初始化連通圖
public static void initGraph(int[][] graph, ArrayList<Integer> points) {
for(int i = 0 ; i < graph.length; i++) {
points.add(i);
for(int j = 0; j < graph[i].length; j++) {
if(i == j) {
graph[i][j] = 10000;
}else {
int temp = (int)(Math.random() * 200 +1);
graph[i][j] = temp; // 大于等于100不連通, 小于100連通
}
graph[j][i] = graph[i][j];
}
}
}
連通圖的數組表示:
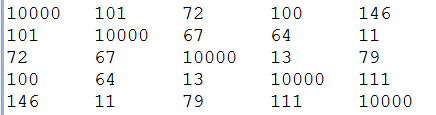
2、找到距離當前樹中節點權重最小的邊,開始節點隨機產生,(算法的重點)!!!
// prime算法實現
public static int prime(int[][] graph, ArrayList<Integer> points, int current) {
String path = "";
ArrayList<Integer> selectPoints = new ArrayList<Integer>(); // 選中的點集合
int totalWeights = 0; // 權重總和
selectPoints.add(current); // 添加初始開始節點
points.remove(current); // 從未選擇的節點集合中刪除被選中的節點
path = "|" + current + "|";
System.out.println("當前路徑:" + path);
System.out.println("當前已選中節點: " + selectPoints.toString());
System.out.println("當前剩余節點: " + points.toString());
System.out.println("當前總權重: " + totalWeights);
// 循環找出最小權重的邊 直至所有的點都被選中
while(points.size() > 0) {
// 遍歷選中的點相連的邊中權重最小的邊記錄下來
int mincost = 0; // 最小權重
int mincostPoint = selectPoints.get(0); // 最小權重邊對應的點
List<Integer> linePoints = new ArrayList<Integer>(); // 記錄所有與已選中點相連的點
for(int i = 0 ; i < selectPoints.size(); i++) {
for(int j = 0; j < points.size(); j++) {
int startPoint = selectPoints.get(i); // 起點
int endPoint = points.get(j); // 終點
// 兩點是相連的
if(graph[startPoint][endPoint] != 10000 && graph[startPoint][endPoint] < 100) {
// 將和已選中點連通的點加入連通集合
linePoints.add(points.get(j));
if(linePoints.size() == 1) {
// 將第一個連通的邊的權重賦值為最小權重
mincost = graph[startPoint][linePoints.get(0)];
// 最小權重相連的點
mincostPoint = endPoint;
}else {
// 與當前的最小權重比較
if(graph[startPoint][endPoint] < mincost) {
// 最小權重相連的點
mincost = graph[startPoint][endPoint];
mincostPoint = endPoint;
}
}
}
}
}
if(mincost != 0) { // 證明是找到了相連的點
selectPoints.add(mincostPoint); // 添加點
points = (ArrayList<Integer>) removeFormPoints(points, mincostPoint);
// 權重增加
totalWeights += mincost;
path += " ---" + mincost + "--- |" + mincostPoint + "|";
System.out.println("當前路徑:" + path);
}else {
System.out.println("不連通");
return 0;
}
// 打印當前所選中的最小權重邊對應的點
System.out.println("當前已選中節點: " + selectPoints.toString());
System.out.println("當前剩余節點: " + points.toString());
System.out.println("當前總權重: " + totalWeights);
}
System.out.println("總路徑:" + path);
// 返回總權重
return totalWeights;
}
// 刪除剩余節點中的相連通的最小權重的節點的方法(就是將該節點加入最小生成樹中)
public static List<Integer> removeFormPoints(ArrayList<Integer> points, int mincostPoint) {
List<Integer> tempPoints = new ArrayList<Integer>();
for(int i = 0; i < points.size(); i++) {
if(points.get(i) != mincostPoint) {
tempPoints.add(points.get(i));
}
}
return tempPoints;
}
以下是算法實現過程的打印信息:
10000 101 72 100 146 101 10000 67 64 11 72 67 10000 13 79 100 64 13 10000 111 146 11 79 111 10000 開始所有節點集:[0, 1, 2, 3, 4] 開始節點:1 當前路徑:|1| 當前已選中節點: [1] 當前剩余節點: [0, 2, 3, 4] 當前總權重: 0 當前路徑:|1| ---11--- |4| 當前已選中節點: [1, 4] 當前剩余節點: [0, 2, 3] 當前總權重: 11 當前路徑:|1| ---11--- |4| ---64--- |3| 當前已選中節點: [1, 4, 3] 當前剩余節點: [0, 2] 當前總權重: 75 當前路徑:|1| ---11--- |4| ---64--- |3| ---13--- |2| 當前已選中節點: [1, 4, 3, 2] 當前剩余節點: [0] 當前總權重: 88 當前路徑:|1| ---11--- |4| ---64--- |3| ---13--- |2| ---72--- |0| 當前已選中節點: [1, 4, 3, 2, 0] 當前剩余節點: [] 當前總權重: 160 總路徑:|1| ---11--- |4| ---64--- |3| ---13--- |2| ---72--- |0| 總權重:160
該算法只是個人的理解實現,若有其他想法或者建議,歡迎大家交流。
更多關于java算法相關內容感興趣的讀者可查看本站專題:《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》
希望本文所述對大家java程序設計有所幫助。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。