您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關python中邏輯回歸的示例分析的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
邏輯回歸也是一種有監督學習方法(supervised machine learning)。邏輯回歸一般用來做預測,也可以用來做分類,預測是某個類別^.^!線性回歸想比大家都不陌生了,y=kx+b,給定一堆數據點,擬合出k和b的值就行了,下次給定X時,就可以計算出y,這就是回歸。而邏輯回歸跟這個有點區別,它是一種非線性函數,擬合功能頗為強大,而且它是連續函數,可以對其求導,這點很重要,如果一個函數不可求導,那它在機器學習用起來很麻煩,早期的海維賽德(Heaviside)階梯函數就因此被sigmoid函數取代,因為可導意味著我們可以很快找到其極值點,這就是優化方法的重要思想之一:利用求導,得到梯度,然后用梯度下降法更新參數。
下面來看看邏輯回歸的sigmoid函數,如(圖一)所示:
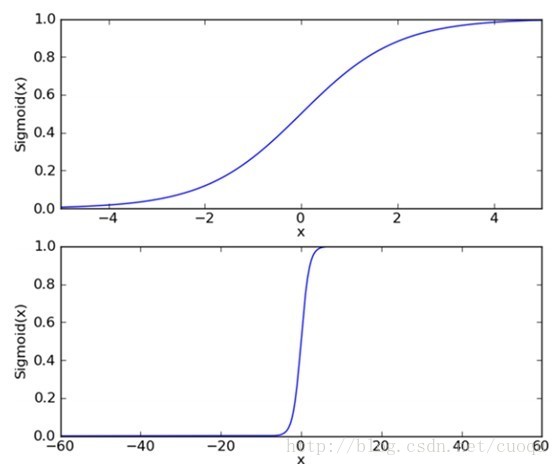
(圖一)
(圖一)中上圖是sigmoid函數在定義域[-5,5] 上的形狀,而下圖是在定義域[-60,60]上的形狀,由這兩個圖可以看出,它比較適合做二類的回歸,因為嚴重兩級分化。Sigmoid函數的如(公式一)所示:
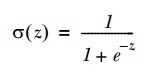
(公式一)
現在有了二類回歸函數模型,就可以把特征映射到這個模型上了,而且sigmoid函數的自變量只有一個Z,假設我們的特征為X=[x0,x1,x2…xn]。令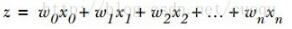 ,當給定大批的訓練樣本特征X時,我們只要找到合適的W=[w0,w1,w2…wn]來正確的把每個樣本特征X映射到sigmoid函數的兩級上,也就是說正確的完成了類別回歸就行了,那么以后來個測試樣本,只要和權重相乘后,帶入sigmoid函數計算出的值就是預測值啦,很簡單是吧。那怎么求權重W呢?
,當給定大批的訓練樣本特征X時,我們只要找到合適的W=[w0,w1,w2…wn]來正確的把每個樣本特征X映射到sigmoid函數的兩級上,也就是說正確的完成了類別回歸就行了,那么以后來個測試樣本,只要和權重相乘后,帶入sigmoid函數計算出的值就是預測值啦,很簡單是吧。那怎么求權重W呢?
要計算W,就要進入優化求解階段咯,用的方法是梯度下降法或者隨機梯度下降法。說到梯度下降,梯度下降一般對什么求梯度呢?梯度是一個函數上升最快的方向,沿著梯度方向我們可以很快找到極值點。我們找什么極值?仔細想想,當然是找訓練模型的誤差極值,當模型預測值和訓練樣本給出的正確值之間的誤差和最小時,模型參數就是我們要求的。當然誤差最小有可能導致過擬合,這個以后再說。我們先建立模型訓練誤差價值函數(cost function),如(公式二)所示:
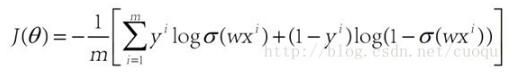
(公式二)
(公式二)中Y表示訓練樣本真實值,當J(theta)最小時的所得的theta就是我們要求的模型權重,可以看出J(theta)是個凸函數,得到的最小值也是全局最小。對其求導后得出梯度,如(公式三)所示:
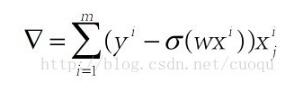
(公式三)
由于我們是找極小值,而梯度方向是極大值方向,因此我們取負號,沿著負梯度方向更新參數,如(公式四)所示:
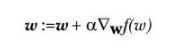
(公式四)
按照(公式四)的參數更新方法,當權重不再變化時,我們就宣稱找到了極值點,此時的權重也是我們要求的,整個參數更新示意圖如(圖二)所示:
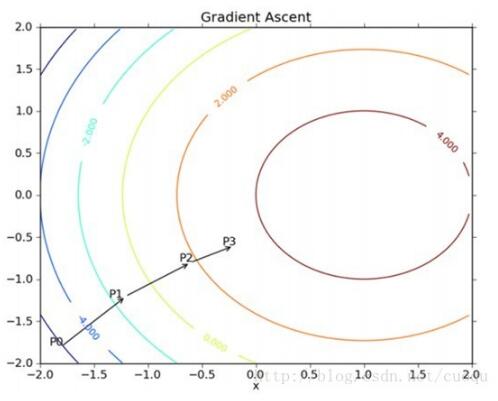
(圖二)
原理到此為止邏輯回歸基本就說完了,下面進入代碼實戰階段:
from numpy import *
def loadDataSet():
dataMat = []; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
def sigmoid(inX):
return 1.0/(1+exp(-inX))上面兩個函數分別是加載訓練集和定義sigmoid函數,都比較簡單。下面發出梯度下降的代碼:
def gradAscent(dataMatIn, classLabels): dataMatrix = mat(dataMatIn) #convert to NumPy matrix labelMat = mat(classLabels).transpose() #convert to NumPy matrix m,n = shape(dataMatrix) alpha = 0.001 maxCycles = 500 weights = ones((n,1)) for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #matrix mult error = (labelMat - h) #vector subtraction weights = weights + alpha * dataMatrix.transpose()* error #matrix mult return weights
梯度下降輸入訓練集和對應標簽,接著就是迭代跟新參數,計算梯度,然后更新參數,注意倒數第二句就是按照(公式三)和(公式四)來更新參數。
為了直觀的看到我們得到的權重是否正確的,我們把權重和樣本打印出來,下面是相關打印代碼:
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()打印的效果圖如(圖三)所示:
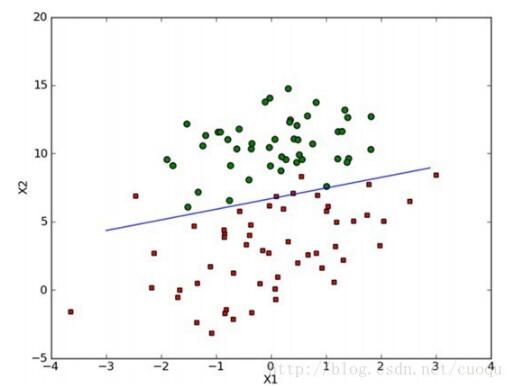
(圖三)
可以看出效果蠻不錯的,小錯誤是難免的,如果訓練集沒有錯誤反而危險,說到這基本就說完了,但是考慮到這個方法對少量樣本(幾百的)還行,在實際中當遇到10億數量級時,而且特征維數上千時,這種方法很恐怖,光計算梯度就要消耗大量時間,因此要使用隨機梯度下降方法。隨機梯度下降算法和梯度下降算法原理一樣,只是計算梯度不再使用所有樣本,而是使用一個或者一小批來計算梯度,這樣可以減少計算代價,雖然權重更新的路徑很曲折,但最終也會收斂的,如(圖四)所示
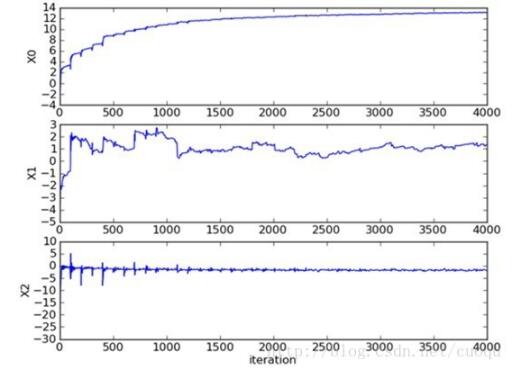
(圖四)
下面也發出隨機梯度下降的代碼:
def stocGradAscent1(dataMatrix, classLabels, numIter=150): m,n = shape(dataMatrix) weights = ones(n) #initialize to all ones for j in range(numIter): dataIndex = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant h = sigmoid(sum(dataMatrix[randIndex]*weights)) error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] del(dataIndex[randIndex]) return weights
最后也給出一個分類的代碼,只要把閾值設為0.5,大于0.5劃為一類,小于0.5劃為另一類就行了,代碼如下:
def classifyVector(inX, weights): prob = sigmoid(sum(inX*weights)) if prob > 0.5: return 1.0 else: return 0.0
感謝各位的閱讀!關于“python中邏輯回歸的示例分析”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。