您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
有一組4096長度的數據,需要找到一階導數從正到負的點,和三階導數從負到正的點,截取了一小段。
394.0
388.0
389.0
388.0
388.0
392.0
393.0
395.0
395.0
394.0
394.0
390.0
392.0
按照之前所了解的,對離散值求導其實就是求差分,例如第i點的導數(差分)為:
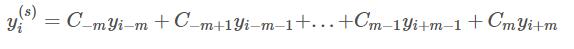
即在一個寬度為2m+1的窗口內通過計算前后m個值加權后的和得到。但是在實際使用過程中效果不是很好。于是想到了同樣在一個寬度為2k+1的窗口內,將這2k+1個點擬合成一個函數,然后求導就可以得到任意階數的導數值。
首先是函數擬合,使用from scipy.optimize import leastsq即最小二乘擬合
from scipy.optimize import leastsq
class search(object):
def __init__(self, filename):
self.filename = filename
def func(self, x, p):
f = np.poly1d(p)
return f(x)
def residuals(self, p, x, y, reg):
regularization = 0.1 # 正則化系數lambda
ret = y - self.func(x, p)
if reg == 1:
ret = np.append(ret, np.sqrt(regularization) * p)
return ret
def LeastSquare(self, data, k=100, order=4, reg=1, show=1): # k為求導窗口寬度,order為多項式階數,reg為是否正則化
l = self.len
step = 2 * k + 1
p = [1] * order
for i in range(0, l, step):
if i + step < l:
y = data[i:i + step]
x = np.arange(i, i + step)
else:
y = data[i:]
x = np.arange(i, l)
try:
r = leastsq(self.residuals, p, args=(x, y, reg))
except:
print("Error - curve_fit failed")
fun = np.poly1d(r[0]) # 返回擬合方程系數
df_1 = np.poly1d.deriv(fun) # 求得導函數
df_2 = np.poly1d.deriv(df_1)
df_3 = np.poly1d.deriv(df_2)
df_value = df_1(x)
df3_value = df_3(x)
fun = np.poly1d(r[0]),fun返回的是一個 polynomial class,具體使用可以見官方文檔numpy.poly1d
polynomial對象可以使用deriv方法求導數,求得的依然是 polynomial對象。 df_value = df_1(x)所得到的就是x這個幾個點求得的導數值。
看似大功告成,但是求導的結果并不是很好,如下圖,實際最高點在100左右,但是擬合出來的曲線最高點在120左右,而原因在于使用多項式擬合很難準確擬合曲線。

于是想用高斯函數來實現對曲線的擬合,在matlab中試了下,三階高斯擬合可以很好的擬合曲線,
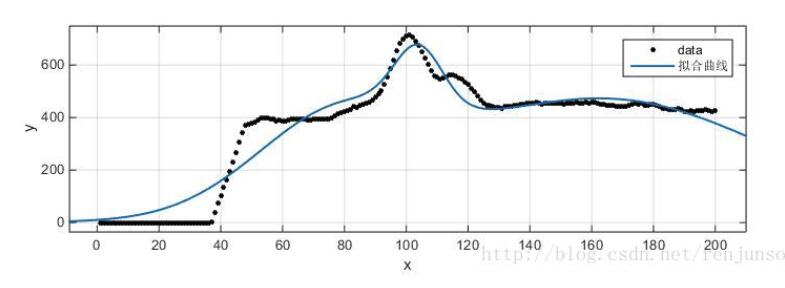
但是numpy以及sicpy中沒有找到類似poly1d這種對象,雖然可以自己定義高斯函數,如下
def gaussian(self, x, *param):
fun = param[0]*np.exp(-np.power(x - param[2], 2.) / (2 * np.power(param[4], 2.)))+param[1]*np.exp(-np.power(x - param[3], 2.) / (2 * np.power(param[5], 2.)))
return fun
但是,在通過最小二乘擬合得到函數參數后只能得到擬合后的點,無法直接求導數..所以并不適合。
所以還是只能回到多項式擬合,如果4階多項式不能表征的話,更高階的呢
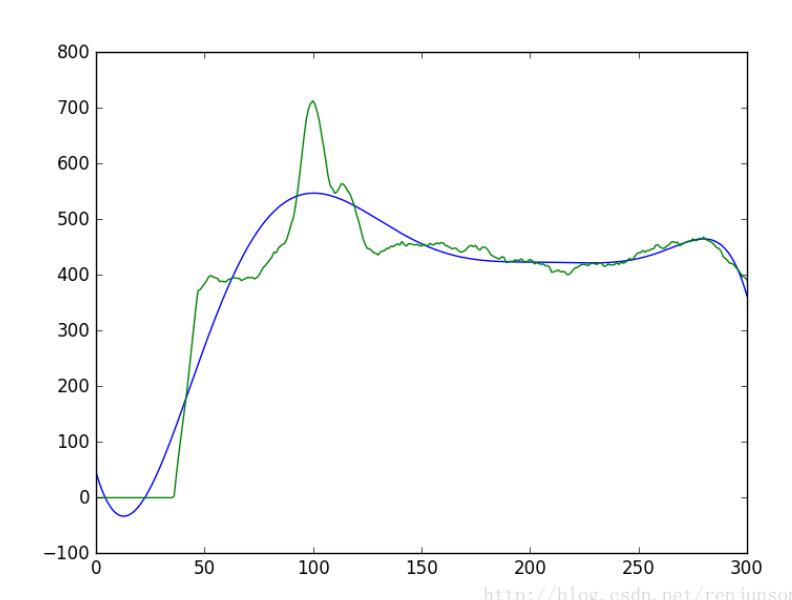
總體來說,效果還是可以接受的。
如果下階段找到好的高斯函數擬合方法,會繼續更新。
以上這篇Python求離散序列導數的示例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。