您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
PCA簡介
主成分分析(Principal Component Analysis,PCA)是最常用的一種降維方法,通常用于高維數據集的探索與可視化,還可以用作數據壓縮和預處理等。矩陣的主成分就是其協方差矩陣對應的特征向量,按照對應的特征值大小進行排序,最大的特征值就是第一主成分,其次是第二主成分,以此類推。
基本步驟:

具體實現
我們通過Python的sklearn庫來實現鳶尾花數據進行降維,數據本身是4維的降維后變成2維,可以在平面中畫出樣本點的分布。樣本數據結構如下圖:

其中樣本總數為150,鳶尾花的類別有三種,分別標記為0,1,2
代碼
import matplotlib.pyplot as plt #加載matplotlib用于數據的可視化 from sklearn.decomposition import PCA #加載PCA算法包 from sklearn.datasets import load_iris data=load_iris() y=data.target x=data.data pca=PCA(n_components=2) #加載PCA算法,設置降維后主成分數目為2 reduced_x=pca.fit_transform(x)#對樣本進行降維 red_x,red_y=[],[] blue_x,blue_y=[],[] green_x,green_y=[],[] for i in range(len(reduced_x)): if y[i] ==0: red_x.append(reduced_x[i][0]) red_y.append(reduced_x[i][1]) elif y[i]==1: blue_x.append(reduced_x[i][0]) blue_y.append(reduced_x[i][1]) else: green_x.append(reduced_x[i][0]) green_y.append(reduced_x[i][1]) #可視化 plt.scatter(red_x,red_y,c='r',marker='x') plt.scatter(blue_x,blue_y,c='b',marker='D') plt.scatter(green_x,green_y,c='g',marker='.') plt.show()
結果圖
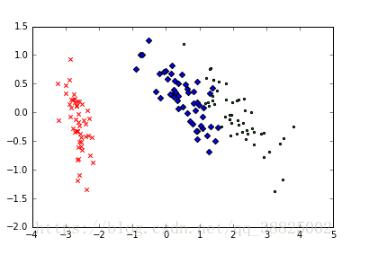
知識拓展:python sklearn PCA 實例代碼-主成分分析
python sklearn decomposition PCA 主成分分析
主成分分析(PCA)
1、主成分分析(Principal Component Analysis,PCA)是最常用的一種降維方法,
通常用于高維數據集的探索與可視化,還可以用作數據壓縮和預處理
2、PCA可以把具有相關性的高維變量合成為線性無關的低維變量,稱為主成分。
主成分能夠盡可能保留原始數據的信息
3、概念
方差:用來度量一組數據的分散程度
協方差:用來度量兩個變量之間的線性相關性程度,若兩個變量的協議差為0,二者線性無關
協方差矩陣:矩陣的特征向量是描述數據集結構的非零向量,?? ⃗=?? ⃗
特征向量和特征值:? ⃗ 特征向量,?是特征值
4、提取:
矩陣的主成分是其協方差矩陣對應的特征向量,按照對應的特征值大小進行排序,最大的特征值就是第一主成分,其次是第二主成分
5、原理:
1、對所有樣本進行中心化:xi-(x1+x2…xm)/m
2、計算樣本的協方差矩陣X(X.T)
3、對協方差矩陣X(X.T)做特征值分解
4、取最大的d個特征值所對應的特征向量w1,w2…wd
輸出投影矩陣W=(w1,w2,…,wd)
6、參數說明
sklearn.decomposition.PCA(n_components=None,copy=True,whithen=False,svd_solver=‘auto',tol=0.0,
iterated_power=‘auto',random_state=None)
n_components:指定主成分的個數,即降維后數據的維度
svd_slover:設置特征值分解的方法:‘full',‘arpack',‘randomized'
PCA實現高維度數據可視化 實例
目標:
已知鳶尾花數據是4維的,共三類樣本,使用PCA實現對鳶尾花數據進行降維,實現在二維平面上的可視化
實例程序編寫
import matplotlib.pyplot as plt import sklearn.decomposition as dp from sklearn.datasets.base import load_iris x,y=load_iris(return_X_y=True) #加載數據,x表示數據集中的屬性數據,y表示數據標簽 pca=dp.PCA(n_components=2) #加載pca算法,設置降維后主成分數目為2 reduced_x=pca.fit_transform(x) #對原始數據進行降維,保存在reduced_x中 red_x,red_y=[],[] blue_x,blue_y=[],[] green_x,green_y=[],[] for i in range(len(reduced_x)): #按鳶尾花的類別將降維后的數據點保存在不同的表表中 if y[i]==0: red_x.append(reduced_x[i][0]) red_y.append(reduced_x[i][1]) elif y[i]==1: blue_x.append(reduced_x[i][0]) blue_y.append(reduced_x[i][1]) else: green_x.append(reduced_x[i][0]) green_y.append(reduced_x[i][1]) plt.scatter(red_x,red_y,c='r',marker='x') plt.scatter(blue_x,blue_y,c='b',marker='D') plt.scatter(green_x,green_y,c='g',marker='.') plt.show()
以上這篇Python sklearn庫實現PCA教程(以鳶尾花分類為例)就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。