您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
廢話不多說,直接上代碼吧!
"""
# 利用 diabetes數據集來學習線性回歸
# diabetes 是一個關于糖尿病的數據集, 該數據集包括442個病人的生理數據及一年以后的病情發展情況。
# 數據集中的特征值總共10項, 如下:
# 年齡
# 性別
#體質指數
#血壓
#s1,s2,s3,s4,s4,s6 (六種血清的化驗數據)
#但請注意,以上的數據是經過特殊處理, 10個數據中的每個都做了均值中心化處理,然后又用標準差乘以個體數量調整了數值范圍。
#驗證就會發現任何一列的所有數值平方和為1.
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
# 增加一個維度,得到一個體質指數數組[[1],[2],...[442]]
diabetes_X = diabetes.data[:, np.newaxis,2]
print(diabetes_X)
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
# 查看相關系數
print('Coefficients: \n', regr.coef_)
# The mean squared error
# 均方差
# 查看殘差平方的均值(mean square error,MSE)
print("Mean squared error: %.2f"
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
# R2 決定系數(擬合優度)
# 模型越好:r2→1
# 模型越差:r2→0
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
對于回歸模型效果的判斷指標經過了幾個過程,從SSE到R-square再到Ajusted R-square, 是一個完善的過程:
SSE(誤差平方和):The sum of squares due to error
R-square(決定系數):Coefficient of determination
Adjusted R-square:Degree-of-freedom adjusted coefficient of determination
下面我對以上幾個名詞進行詳細的解釋下,相信能給大家帶來一定的幫助!!
一、SSE(誤差平方和)
計算公式如下:
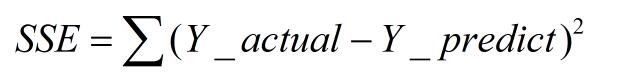
同樣的數據集的情況下,SSE越小,誤差越小,模型效果越好
缺點:
SSE數值大小本身沒有意義,隨著樣本增加,SSE必然增加,也就是說,不同的數據集的情況下,SSE比較沒有意義
二、R-square(決定系數)
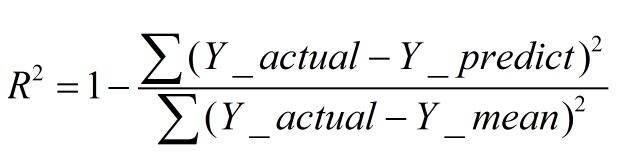
數學理解: 分母理解為原始數據的離散程度,分子為預測數據和原始數據的誤差,二者相除可以消除原始數據離散程度的影響
其實“決定系數”是通過數據的變化來表征一個擬合的好壞。
理論上取值范圍(-∞,1], 正常取值范圍為[0 1] ------實際操作中通常會選擇擬合較好的曲線計算R²,因此很少出現-∞
越接近1,表明方程的變量對y的解釋能力越強,這個模型對數據擬合的也較好
越接近0,表明模型擬合的越差
經驗值:>0.4, 擬合效果好
缺點:
數據集的樣本越大,R²越大,因此,不同數據集的模型結果比較會有一定的誤差
三、Adjusted R-Square (校正決定系數)
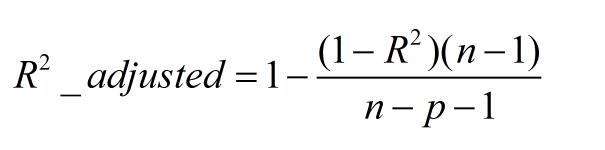
n為樣本數量,p為特征數量
消除了樣本數量和特征數量的影響
以上這篇Python 線性回歸分析以及評價指標詳解就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。