您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
下面這段代碼是我定義的Stack類模板,接下來介紹幾種用2個該Stack類實現隊列Queue的幾種方法。
template<class T, int DEFAULT_CAPACITY = 0>
class Stack
{
public:
Stack();
Stack(const Stack<T> &st);
Stack &operator=(const Stack<T> &st);
~Stack();
public:
void Push(const T &data);
void Pop();
T &Top();
T &End();
bool Empty();
size_t Size();
void Print();
protected:
void CheckCapacity();
protected:
T *_arr;
size_t _top;
size_t _capacity;
};聲明:為了實現除“入隊”“出隊”之外更多的功能,比如“打印”等,我將上面那個已造好的“輪子”Stack做了擴展,增加了一些成員方法。而如果你關注的重點是push和pop的算法,那么其實并不需要在意我造的下面這個“輪子”。可以直接跳過下面的代碼,并把所有我使用的Stack類型當作庫里的stack即可.
擴展后的Stack:
template<class T, int DEFAULT_CAPACITY = 0>
class Stack
{
public:
Stack()
:_arr(NULL)
, _top(0)
, _capacity(0)
{}
Stack(const Stack<T> &st)
:_arr(new T[st._capacity])
, _top(st._top)
, _capacity(st._capacity)
{
for (size_t i = 0; i < _capacity; i++)
{
_arr[i] = st._arr[i];
}
}
Stack &operator=(const Stack<T> &st)
{
if (st._arr != _arr)
{
delete[] _arr;
_arr = new T[st._capacity];
for (size_t i = 0; i < st._capacity; i++)
{
_arr[i] = st._arr[i];
}
_top = st._top;
_capacity = st._capacity;
}
return *this;
}
~Stack()
{
if (_arr != NULL)
{
delete[] _arr;
}
}
public:
void Push(const T &data)
{
CheckCapacity();
_arr[_top] = data;
++_top;
}
void Pop()
{
--_top;
}
T &Top()
{
return _arr[_top - 1];
}
T &End()
{
return _arr[0];
}
bool Empty()
{
if (0 == _top)
{
return true;
}
else
{
return false;
}
}
size_t Size()
{
return _top;
}
void Print()
{
for (size_t i = 0; i < _top; i++)
{
cout << _arr[i] << " ";
}
cout << endl;
}
void RePrint()
{
if (0 == _top)
{
return;
}
for (int i = _top - 1; i >= 0; i--)
{
cout << _arr[i] << " ";
}
cout << endl;
}
protected:
void CheckCapacity()
{
if (_top == _capacity)
{
_capacity = _capacity + 3;
T *tmp = new T[_capacity];
for (size_t i = 0; i < _top; i++)
{
tmp[i] = _arr[i];
}
delete[] _arr;
_arr = tmp;
}
}
protected:
T *_arr;
size_t _top;
size_t _capacity;
};--------------------------------------------------------------------------------
一、普通版本
棧的特點是“先入后出”,而隊列的特點是“先入先出”。
所以可以定義一個類Queue,包含2個成員對象:
一個棧_stack1存放數據,另一個棧_stack2用來臨時存放數據,通過一些壓棧出棧的成員方法就可以實現對隊列的入隊、出隊操作。
實現的2個棧組成的隊列如下圖所示,現在要將一組數據【1 2 3 4 5】放入隊列中:
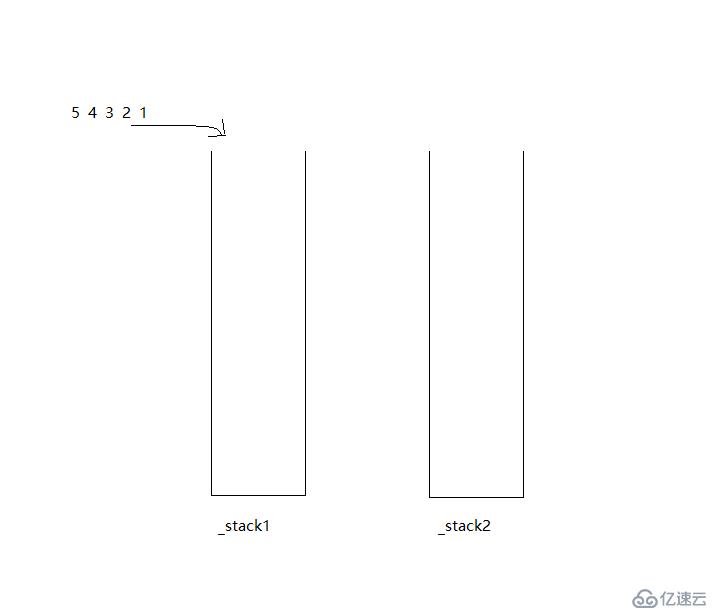
先將這組數依次壓入_stack1中,然后再將_stack1中的元素依次出棧壓入_stack2中:
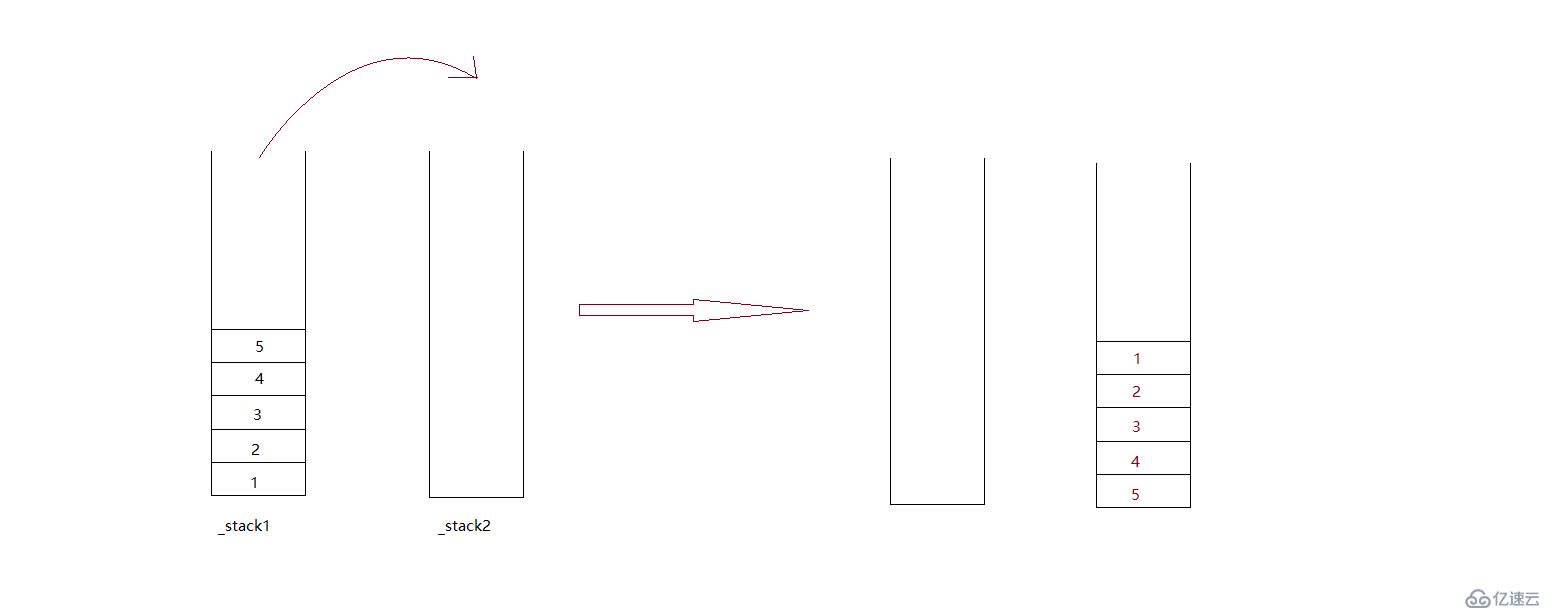
這時候,_stack2中的元素依次出棧,就相當于隊列的出隊操作了。
用代碼實現:
定義一個類模板Queue:
template<class T>
class Queue
{
Queue()
:_size(0)
{}
void Push(const T &data) //入隊
{
_stack1.Push(data);
++_size;
}
void Pop() //出隊
{
Converse(_stack2, _stack1);
_stack2.Pop();
Converse(_stack1, _stack2);
--_size;
}
protected:
void Converse(Stack<T> &dst, Stack<T> &src) //src->dst
{
while (size--)
{
dst.Push(src.Top());
src.Pop();
}
}
protected:
Stack<T> _stack1;
Stack<T> _stack2;
size_t _size;
};其中,
成員方法Converse():作用是將棧src中的內容依次出棧,壓入棧dst中。
成員方法Push() :入隊操作,每次將元素data存入成員對象_stack1中。
成員方法Pop() :出隊操作,彈出第一個送入的元素。其中,第二個Converse的作用是還原。
可以看出,這種入隊、出隊的算法,需要保證元素始終在_stack1中維護,而只有在出棧的時候用到_stack2臨時存放數據。
采用這種方式實現的隊列,可以實現正常的入隊、出隊操作,但應該注意到,其中出隊操作需要進行兩次壓棧,我們可以對一個細節稍作優化,進一步提高出隊操作的執行效率。
下圖為優化后的出隊操作:
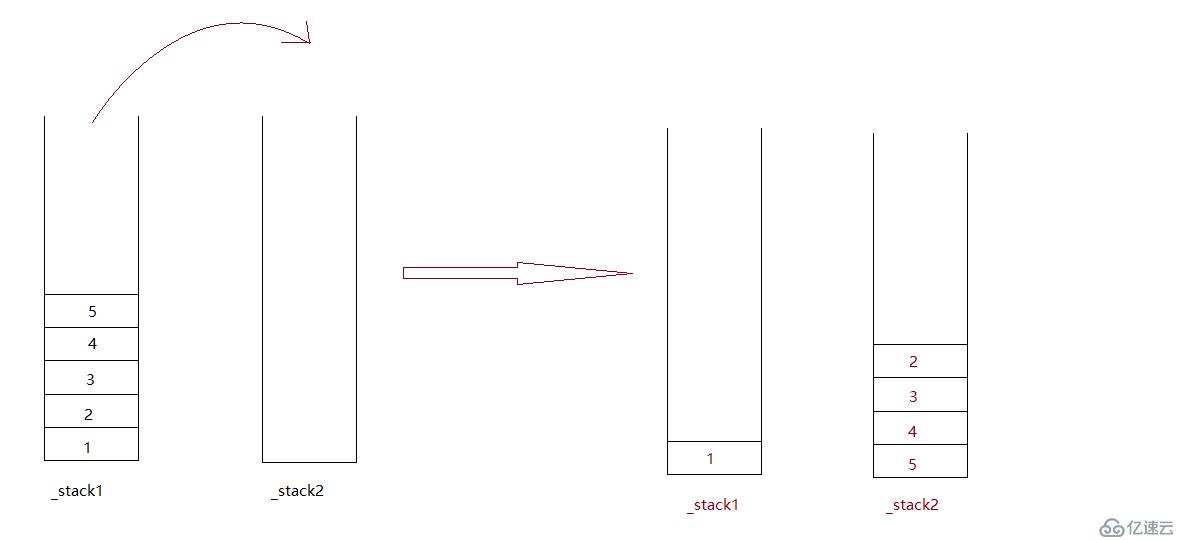
區別在于,在出隊操作時,將_stack1中的(_size - 1)個元素彈出并壓入_stack2中。
彈出后,也不需要將_stack2的元素“倒回”_stack1中。
二、代碼優化
具體的實現步驟為:
出隊操作時:
而是在每次執行出隊的時候進行一次判斷:
若_stack2為空,則將_stack1中的(_size - 1)個元素彈出并壓入_stack2中,并彈出_stack中剩下的那個元素(就是我上面說的那個步驟);
若_stack2不為空,則彈出_stack2中最頂層的元素。
在入隊操作時,判斷_stack1是否為空:
若為空,則先將_stack2中的元素依次彈出并壓入_stack1中,然后再將入棧元素壓入_stack1中(左圖)
否則,直接將入棧元素壓入_stack1中
優化后的方案用代碼實現如下:
template<class t>
class queue
{
public:
queue()
:_size(0)
{}
queue(const queue &que)
{
_stack1 = que._stack1;
_size = que._size;
}
public:
void Push(const t &data)
{
if (_stack1.Empty() && !_stack2.Empty())
{
Converse(_stack1, _stack2);
}
_stack1.Push(data);
++_size;
}
void Pop()
{
if (_stack2.Empty())
{
if (_stack1.Empty())
{
return;
}
RemainConverse(_stack2, _stack1);
_stack1.Pop();
}
else
{
_stack2.Pop();
}
--_size;
}
void Print()
{
_stack1.Print();
_stack2.RePrint();
}
bool Empty()
{
return (0 == _size);
}
t& Front()
{
if (_stack1.empty())
{
return _stack2.top();
}
else
{
return _stack1.end();
}
}
t& Back()
{
if (_stack1.Empty())
{
return _stack2.End();
}
else
{
return _stack1.Top();
}
}
size_t Size()
{
return _size;
}
protected:
void RemainConverse(Stack<t> &dst, Stack<t> &src)
{
size_t count = src.Size() - 1;
while (count--)
{
dst.Push(src.Top());
src.Pop();
}
}
void Converse(Stack<t> &dst, Stack<t> &src) //src->dst
{
while (!src.Empty())
{
dst.Push(src.Top());
src.Pop();
}
}
protected:
Stack<t> _stack1;
Stack<t> _stack2;
size_t _size;
};
int main()
{
queue<int> que1;
que1.Push(1);
que1.Push(2);
que1.Push(3);
que1.Push(4);
que1.Print();
que1.Pop();
que1.Print();
que1.Push(5);
que1.Print();
return 0;
}到目前我們已經實現了2種不同的方式實現這個隊列。
這兩種方法相比,第一種方法每次進行出隊操作都要移動2次棧中的全部數據
而對于第二種方法實現的隊列,如果連續進行入隊或者出隊操作,則不需要移動2個棧中的數據,能一定程度上提高效率。
三、進一步優化
可以看出,_stack1和_stack2中全部元素(或者說,全部元素-1)轉移的次數越少,程序的執行效率就越高。
還有一種方法可以進一步減少_stack1和_stack2中全部元素交換的次數:
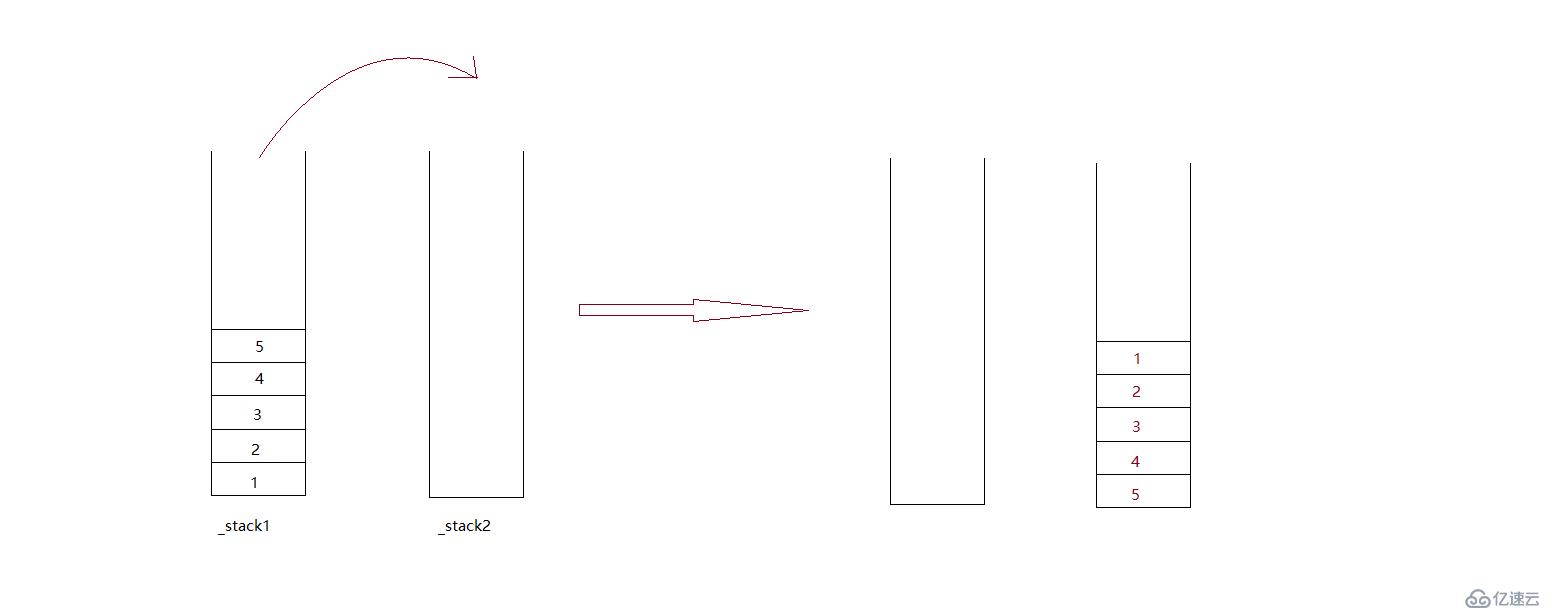 出隊:
出隊:
檢測_stack2是否為空:
若為空,則將_stack1中的元素依次彈出并壓入_stack2中,
若不為空,則彈出_stack2中棧頂的元素
入隊:
將元素壓入_stack。
可以看出,這種實現方式入隊永遠是從_stack2中彈出元素,出隊永遠是向_stack1中壓入元素
而只有當入棧時檢測到_stack2為空時,才執行2個棧之間全部元素的轉移。
用如下的圖能更形象地表示:
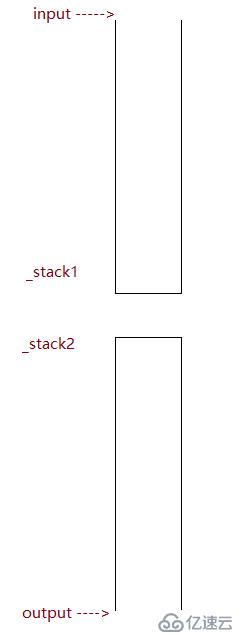
實現代碼如下:
template<class T>
class Queue
{
public:
Queue()
:_size(0)
{}
Queue(const Queue &que)
{
_stack1 = que._stack1;
_size = que._size;
}
public:
void Push(const T &data)
{
_stack1.Push(data);
++_size;
}
void Pop()
{
if (_size == 0) //異常
{
return;
}
if (_stack2.Empty())
{
Converse(_stack2, _stack1);
}
_stack2.Pop();
--_size;
}
void Print()
{
_stack2.RePrint();
_stack1.Print();
}
bool Empty()
{
return (0 == _size);
}
T& Front()
{
if (_stack2.Empty())
{
return _stack2.End();
}
else
{
return _stack2.Top();
}
}
T& Back()
{
return _stack1.Top();
}
size_t Size()
{
return _size;
}
protected:
void Converse(Stack<T> &dst, Stack<T> &src)
{
while (!src.Empty())
{
dst.Push(src.Top());
src.Pop();
}
}
protected:
Stack<T> _stack1;
Stack<T> _stack2;
size_t _size;
};四、總結
這里一共提供了3種方法:
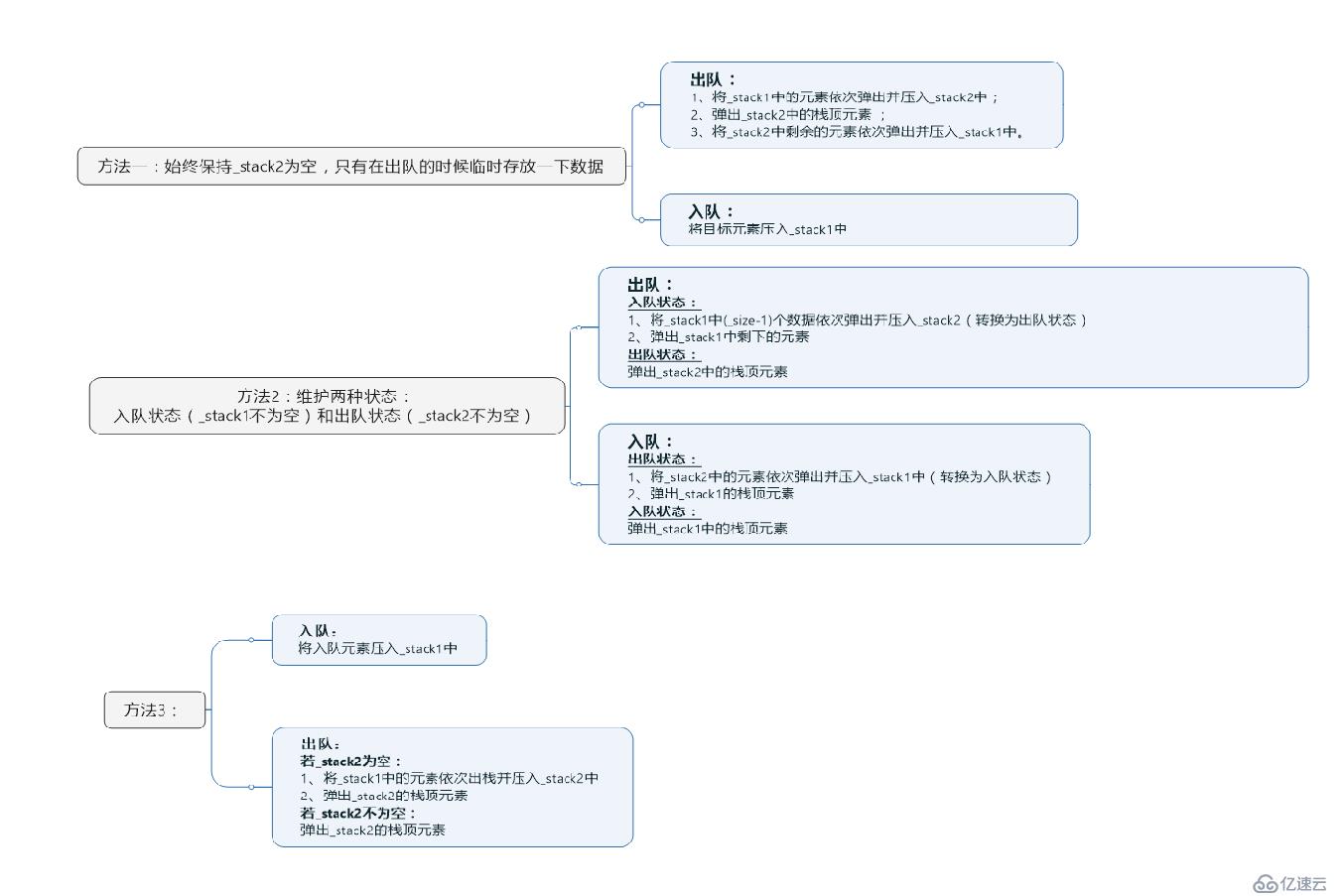
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。