遞歸與非遞歸實現二叉樹

    二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”和“右子樹”。二叉樹的每個結點至多只有二棵子樹(不存在度大于2的結點)，二叉樹的子樹有左右之分，次序不能顛倒。二叉樹的第i層至多有2^（i - 1）個結點；深度為k的二叉樹至多有2^k - 1個結點。由于樹的定義是遞歸實現的，所以在進行二叉樹的前序、中序和后序遍歷可通過遞歸實現，但也可通過非遞歸的棧來實現，二叉樹的層次遍歷可通過隊列實現。

下面我對二叉樹及前序、中序、后序遍歷二叉樹等方法進行實現

例如二叉樹:

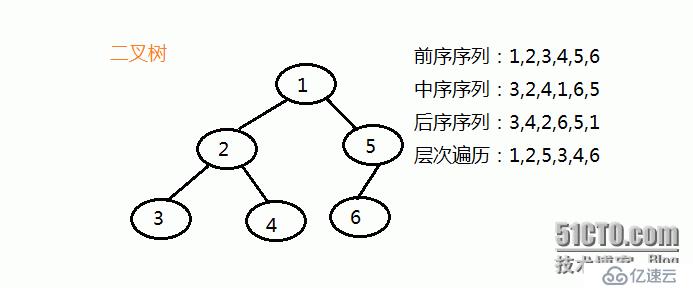
測試用例：

int arrary[10] = {1,2,3,'$','$',4,'$','$',5,6};

arrary為上圖所示二叉樹，通過前序存儲的，'$'表示非法值，即沒有結點

二叉樹的結構：

template<class T>
struct BinaryTreeNode
{
	BinaryTreeNode<T>* _left;
	BinaryTreeNode<T>* _right;
	T _data;
	BinaryTreeNode();
	BinaryTreeNode(const T& x);
};

template<class T>
class BinaryTree
{
	typedef BinaryTreeNode<T> Node;
public:
	BinaryTree();
	BinaryTree(const T* a, size_t size, const T& invalid);
	BinaryTree(const BinaryTree<T>& t);
	BinaryTree<T>& operator=(BinaryTree<T> t);
	~BinaryTree();
	void PrevOrder();//前序遍歷-遞歸	
	void InOrder();//中序遍歷-遞歸
	void PostOrder();//后序遍歷-遞歸
	void PrevOrder_NonR();//前序遍歷-非遞歸
	void InOrder_NonR();//中序遍歷-非遞歸
	void PostOrder_NonR();//后序遍歷-非遞歸
	void LevelOrder();//層次遍歷
	size_t Size();//結點個數
	size_t Depth();//樹的深度
	size_t LeafSize();//葉子結點個數
	size_t GetkLevel();//第k層結點個數
protected:
	Node* _CreateTree(const T* a, size_t size, size_t& index, const T& invalid);//樹的建立
	Node* _CopyTree(Node* t);//復制樹
	void _Distory(Node* root);//清空結點，先釋放子樹，再釋放根結點
	void _PrevOrder(Node* root);//前序遍歷
	void _InOrder(Node* root);//中序遍歷
	void _PostOrder(Node* root);//后序遍歷
	size_t _Size(Node* root);//結點個數
	size_t _Depth(Node* root);//樹的深度
	//size_t _LeafSize(Node* root);//葉子結點個數
	size_t _LeafSize(Node* root,size_t& size);//葉子結點個數
	//size_t _GetkLevel(int k, Node* root);//第k層結點個數
	size_t _GetkLevel(int k, Node* root, int& size, int level);//第k層結點個數
private:
	Node* _root;// BinaryTreeNode<T>* _root;
};

二叉樹的構造、拷貝構造、賦值運算和析構的實現，由于二叉樹存在左子樹和右子樹，故用遞歸實現其功能，具體實現如下：

template<class T>
BinaryTreeNode<T>::BinaryTreeNode()
:_left(NULL)
, _right(NULL)
, _data(0)
{}
template<class T>
BinaryTreeNode<T>::BinaryTreeNode(const T& x)
: _left(NULL)
, _right(NULL)
, _data(x)
{}

template<class T>
BinaryTree<T>::BinaryTree()
:_root(NULL)
{}
template<class T>
BinaryTree<T>::~BinaryTree()
{
	_Distory(_root);
}
template<class T>
void BinaryTree<T>::_Distory(Node* root)//清空結點，先釋放子樹，再釋放根結點
{
	if (root == NULL)
	{
		return;
	}
	if (root->_left)//遞歸釋放子結點
	{
		_Distory(root->_left);
	}
	if (root->_right)
	{
		_Distory(root->_right);
	}
	delete root;
	root = NULL;
}
template<class T>
BinaryTree<T>::BinaryTree(const T* a, size_t size, const T& invalid)
{
	size_t index = 0;//標記數組下標
	_root = _CreateTree(a, size, index, invalid);
}
template<class T>
BinaryTreeNode<T>* BinaryTree<T>::_CreateTree(const T* a, size_t size, size_t& index, const T& invalid)//樹的建立
{
	Node* root = NULL;
	if (index < size && a[index] != invalid)//indx<size以防數組越界
	{
		root = new Node(a[index]);
		root->_left = _CreateTree(a, size, ++index, invalid);//左子樹遞歸
		root->_right = _CreateTree(a, size, ++index, invalid);//右子樹遞歸
	}
	return root;
}
template<class T>
BinaryTree<T>::BinaryTree(const BinaryTree<T>& t)
{
	_root = _CopyTree(t._root);
}
template<class T>
BinaryTreeNode<T>* BinaryTree<T>::_CopyTree(Node* t)//此處的返回類型不能用Node表示
{
	Node* root = NULL;
	if (t != NULL)
	{
		root = new Node(t->_data);
		root->_left = _CopyTree(t->_left);
		root->_right = _CopyTree(t->_right);
	}
	return root;
}
template<class T>
BinaryTree<T>& BinaryTree<T>::operator=(BinaryTree<T> t)//現代寫法
{
	if (this != &t)
	{
		BinaryTree<T> tmp = t;
		swap(_root, tmp._root);
	}
	return *this;
}

前序遍歷(先根遍歷)：(1)先訪問根節點；(2)前序訪問左子樹；(3)前序訪問右子樹.【1 2 3 4 5 6】

下面分別用遞歸和非遞歸兩種方法實現。

二叉樹的遞歸實現前序遍歷

//遞歸實現
template<class T>
void BinaryTree<T>::PrevOrder()//前序遍歷(先根結點)
{
	_PrevOrder(_root);
}
template<class T>
void BinaryTree<T>::_PrevOrder(Node* root)
{
	if (root == NULL)
	{
		return;
	}
	cout << root->_data << " ";
	_PrevOrder(root->_left);
	_PrevOrder(root->_right);
}

二叉樹的非遞歸實現前序序列，利用棧實現。

由于棧是后進先出，對于二叉樹的前序遍歷先訪問左子樹后訪問右子樹，故右結點比左結點先進棧

//非遞歸實現（利用棧實現）
template<class T>
void BinaryTree<T>::PrevOrder_NonR()//前序遍歷-非遞歸
{
	stack<Node*> s;
	if (_root)
	{
		s.push(_root);
	}
	while (!s.empty())
	{
		Node* top = s.top();//訪問棧頂元素
		cout << top->_data << " ";
		s.pop();
		//右結點比左結點先進棧
		if (top->_right)
		{
			s.push(top->_right);
		}
		if (top->_left)
		{
			s.push(top->_left);
		}
	}
	cout << endl;
}

中序遍歷：(1)中序訪問左子樹；(2)訪問根節點；(3)中序訪問右子樹.【3 2 4 1 6 5】

下面分別用遞歸和非遞歸兩種方法實現

二叉樹的遞歸實現中序序列

template<class T>
void BinaryTree<T>::InOrder()//中序遍歷（中根結點）
{
	_InOrder(_root);
}
template<class T>
void BinaryTree<T>::_InOrder(Node* root)
{
	if (root == NULL)
	{
		return;
	}
	_InOrder(root->_left);
	cout << root->_data << " ";
	_InOrder(root->_right);
}

二叉樹的非遞歸實現中序序列

//非遞歸實現（利用棧實現）
template<class T>
void BinaryTree<T>::InOrder_NonR()//中序遍歷-非遞歸
{
	if (_root == NULL)
	{
		return;
	}
	stack<Node*> s;
	Node* cur = _root;
	while (cur || !s.empty())
	{
		//壓一棵樹的左結點，直到最左結點
		while (cur)
		{
			s.push(cur);
			cur = cur->_left;
		}
		if (!s.empty())
		{
		    Node* top = s.top();
		    cout << top->_data << " ";
		    s.pop();
			cur = top->_right;//使cur指向最左結點top的右結點
		}
	}
	cout << endl;
}

后序遍歷(后根遍歷)：(1)后序訪問左子樹；(2)后序訪問右子樹；(3)訪問根節點.【3 4 2 6 5 1】

下面分別用遞歸和非遞歸兩種方法實現

二叉樹的遞歸實現后序序列

//遞歸實現
template<class T>
void BinaryTree<T>::PostOrder()//后序遍歷（后根結點）
{
	_PostOrder(_root);
}
template<class T>
void BinaryTree<T>::_PostOrder(Node* root)//后序遍歷
{
	if (root == NULL)
	{
		return;
	}
	_PostOrder(root->_left);
	_PostOrder(root->_right);
	cout << root->_data << " ";
}
//非遞歸實現（利用棧實現）

二叉樹的非遞歸實現后序序列

template<class T>
void BinaryTree<T>::PostOrder_NonR()//后序遍歷-非遞歸
{
	if (_root == NULL)
	{
		return;
	}
	stack<Node*> s;
	Node* cur = _root;
	Node* prev = NULL;
	while (cur || !s.empty())
	{
		//壓一棵樹的左結點，直到最左結點
		while (cur)
		{
			s.push(cur);
			cur = cur->_left;
		}
		Node* top = s.top();
		if (top->_right == NULL || top->_right == prev)
		{
			cout << top->_data << " ";
			s.pop();
			prev = top;
		}
		else//當未訪問過棧頂的右子樹，則繼續右子樹的訪問
		{
			cur = top->_right;
		}
		cout << endl;
	}
}

層序遍歷：一層層節點依次遍歷。【1 2 5 3 4 6】

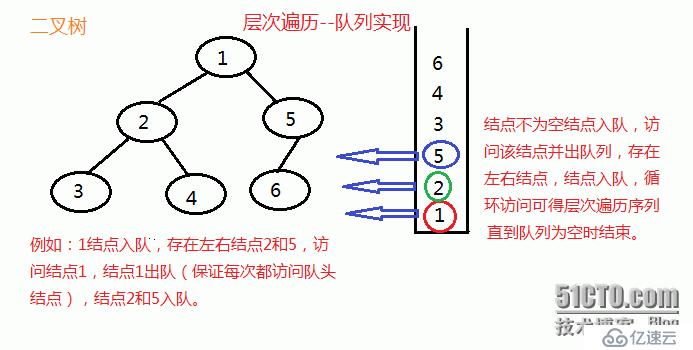
下面用非遞歸方法實現，利用隊列進行訪問。

//遞歸實現
template<class T>
void BinaryTree<T>::LevelOrder()//層次遍歷,通過隊列實現
{
	queue<Node*> q;//建立隊列存放Note*類型值
	if (_root != NULL)
	{
		q.push(_root);
	}
	while (!q.empty())
	{
		Node* front = q.front();
		cout << front->_data << " ";//訪問隊頭
		q.pop();//隊頭出隊列
		if (front->_left != NULL)//存在左或右結點入隊列
		{
			q.push(front->_left);
		}
		if (front->_right != NULL)
		{
			q.push(front->_right);
		}
	}
	cout << endl;
}

求樹的結點個數，遞歸實現：

template<class T>
size_t BinaryTree<T>::Size()//結點個數
{
	return _Size(_root);
}
template<class T>
size_t BinaryTree<T>::_Size(Node* root)
{
	if (root == NULL)
	{
		return 0;
	}//root不為0，則Size+1
	return _Size(root->_left) + _Size(root->_right) + 1;
}

求樹的深度，遞歸實現：

template<class T>
size_t BinaryTree<T>::Depth()//樹的深度
{
	return _Depth(_root);
}
template<class T>
size_t BinaryTree<T>::_Depth(Node* root)
{
	if (root == NULL)
	{
		return 0;
	}
	size_t LeftDepth = _Depth(root->_left);
	size_t RightDepth = _Depth(root->_right);
	if (LeftDepth > RightDepth)//root不為0，則深度+1
	{
		return LeftDepth + 1;
	}
	else
	{
		return RightDepth + 1;
	}
}

求樹的葉子結點個數，遞歸實現：

//方法一
template<class T>
size_t BinaryTree<T>::LeafSize()//葉子結點個數
{
	return _LeafSize(_root);
}
template<class T>
size_t BinaryTree<T>::_LeafSize(Node* root)
{
	if (root == 0)
	{
		return 0;
	}
	if (root->_left == 0 && root->_right == 0)
	{
		return 1;
	}
	return _LeafSize(root->_left) + _LeafSize(root->_right);
}
//方法二:在LeafSize中定義_size表示葉子結點個數
template<class T>
size_t BinaryTree<T>::LeafSize()//葉子結點個數
{
	size_t _size = 0;
	return _LeafSize(_root, _size);
}
template<class T>
size_t BinaryTree<T>::_LeafSize(Node* root, size_t& size)
{
	if (root == 0)
	{
		return 0;
	}
	if (root->_left == 0 && root->_right == 0)
	{
		++size;
		return size;
	}
	_LeafSize(root->_left, size);
	_LeafSize(root->_right, size);
	return size;
}

二叉樹中第k層結點的個數，遞歸實現：

//方法一
template<class T>
size_t BinaryTree<T>::GetkLevel(int k)
{
        assert(k>0);
	return _GetkLevel(k, _root);
}
template<class T>
size_t BinaryTree<T>::_GetkLevel(int k, Node* root)//第k層結點個數
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)//利用遞歸使k遞減，k==1結束
	{
		return 1;
	}
	size_t size1 = _GetkLevel(k - 1, root->_left);
	size_t size2 = _GetkLevel(k - 1, root->_right);
	return size1 + size2;
}
//方法二:在GetkLevel中定義size表示第k層結點個數
template<class T>
size_t BinaryTree<T>::GetkLevel(int k)
{
	assert(k > 0);
	int size = 0;//size為二叉樹第level層結點個數
	int level = 1;//第level層
	return _GetkLevel(k, _root, size, level);
}
template<class T>
size_t BinaryTree<T>::_GetkLevel(int k, Node* root, int& size, int level)//第k層結點個數
{
	if (root == NULL)
	{
		return 0;
	}
	if (level == k)
	{
		++size;
		return size;
	}
	_GetkLevel(k, root->_left, size, level+1);
	_GetkLevel(k, root->_right, size, level+1);
	return size;
}