Java位運算實現方法

不借助中間變量交換兩個變量的值

通常情況下，我們要交換兩個變量的值都按如下步驟操作：

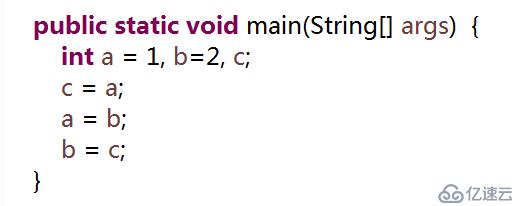
這種操作方式不難理解，實現交換變量值的關鍵點就在于中間變量c。而現在的題目要求是不借助中間變量來交換a和b的值。如果不使用位運算的方式，同樣可以做到不借助中間變量交換兩個變量的值，其實現過程如下。

為了講解方便，我們把最初a與b的值稱之為原始a和原始b，3行代碼就是3步操作：
第1步：把原始a與原始b相加的和存儲到變量a中，變量b的值暫時沒有發生變化。
第2步：用這個和減去原始b，再賦值到變量b中，經過這一步運算，變量b中就保存了原始a的值。
第3步：用原始a、b之和減去原始a的值，就得到原始b，并且把這個值保存到變量a中。
通過以上3步就實現了a、b兩個變量在不借助中間變量的情況下進行值的交換。這種算法雖然沒有借助中間變量，但有一個問題是如果a和b都是較大的數，在做第1步操作的時候就有可能出現兩值相加的和超出int類型的最大值，產生溢出的現象，從而導致后面的運算全部出錯。
而我們用位運算的方式實現交換，就不存在這個問題了。具體代碼如下：

講述這段代碼之前，先回顧一個運算規律，那就是：a^b^b的運算結果等于a。對此運算規律有疑義，請閱讀《Java千問：Java語言位運算符詳解》一文。為了表述方便，我們把a^b的操作稱之為”用b對a加密”，之所以這么稱呼，就是因為a與b進行了異或運算之后，得到一個全新的值，效果如同對a加密一樣。而把a^b^b的操作稱之為”還原”， 之所以這么稱呼，就是因為a^b^b的運算結果等于a，如同是把a的值”加密”之后，又進行了還原，恢復了a的值。
我們還是把a和b最初的值稱為原始a和原始b。這三行代碼是如何實現變量值交換的呢？我們逐行講解：
第1行代碼：對a用b進行了加密操作，并且又賦值給了變量a，此時變量a就由原始數據變成了加密后的值。
第2行代碼：把加密后的值與原始b進行異或運算，就還原了原始a的值，我們把這個值賦值給b，這樣變量b中就存儲了原始a的值。
第3行代碼：用加密后的值與現在的b，也就是保存了原始a的變量進行異或操作，就能得到原始b的值，之后再把原始b的值賦值給變量a，這樣就完成了變量a與b值的交換。

找出單身狗元素

所謂找出單身狗元素就是指：一個數組中，某個數只出現了一次，而其他數都出現了兩次，要求編寫程序把那個只出現了一次的數找出來。完成這個題目的最核心原理就是: 兩個相同的數字進行異或運算，結果為0，而任何一個整數與0進行異或運算，其結果都是這個數本身。另外，任意N個整數進行異或操作，滿足交換律。
按照這個思路，我們只需要把數組中所有的元素都做一遍異或操作，所得到的值就是那個只出現了一次的數字。因為出現了兩次的數字，它們之間進行異或操作會變為0。即使這兩個數字沒有挨在一起，但根據異或運算的交換律我們可以知道：位置關系并不影響運算結果，所以兩個相同的數字只要都參與了異或運算，最終的結果都是0。而那個只出現了一次的數字，與0進行異或操作，其結果仍然是它自身的值。因此，異或運算的結果就是那個只出現了一次的數字，我們根據異或運算的結果，就能找出”單身狗”元素了。具體實現代碼如下：

這道題目還有另一個版本，題目描述為：有整型數組a和b，a數組中所有元素都出現在b數組中，但b數組比a數組多出一個元素，編寫程序找到b數組中多出來的這個元素。雖然變成了兩個數組，但實現算法的思路并沒有發生變化，只是由原來的一個數組全部元素參與異或運算，變成了兩個數組中的元素都要參與異或運算，其實現代碼如下：