您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“Python中怎么使用sklearn進行特征降維”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
0維 標量
1維 向量
2維 矩陣
概念
降維是指在某些限定條件下,降低隨機變量(特征)個數,得到一組“不相關”主變量的過程
注:正是因為在進行訓練的時候,我們都是使用特征進行學習,如果特征本身存在問題或者特征之間相關性較強,對于算法學習預測會影響較大
降維的兩種方式:
特征選擇主成分分析(可以理解為一種特征提取的方式)
①定義
數據中包含冗余或相關變量(或稱特征、屬性、指標等),旨在從原有特征中找出主要特征。
②方法
Filter(過濾式):主要探究特征本身特點、特征與特征和目標值之間關聯
方差選擇法:低方差特征過濾
相關系數
Embedded(嵌入式):算法自動選擇特征(特征與目標值之間的關聯)
決策樹:信息熵、信息增益
正則化:L1、L2
深度學習:卷積等
③模塊
sklearn.feature_selection
刪除低方差的一些特征
特征方差小:某個特征很多樣本的值比較相近
特征方差大:某個特征很多樣本的值都有差別
API
sklearn.feature_selection.VarianceThreshold(threshold=0.0)
-刪除所有低方差特征
-Variance.fit_transform(X)
X:numpy array格式的數據[n_samples,n_features]
返回值:訓練集差異低于threshold的特征將被刪除。默認值是保留所有非零方差特征,即刪除所有樣本中具有相同值的特征
代碼演示
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
def variance_demo():
#1.獲取數據
data=pd.read_csv("data.TXT")
print("data:\n", data)
#2.實例化一個轉換器類
transfer=VarianceThreshold(threshold=7)
#3.調用fit_transform
result=transfer.fit_transform(data)
print("result:\n", result,result.shape)
return None皮爾遜相關系數(Pearson Correlation Coefficient)
反映變量之間相關關系密切程度的統計指標
公式
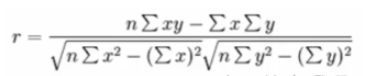
特點
相關系數的值介于-1與+1之間,即-1<=r<=+1,其性質如下:
當r>0時,表示兩變量正相關,r<0時,兩變量為負相關
當|r|=1時,表示兩變量為完全相關,當r=0時,表示兩變量間無相關關系
當0<|r|<1時,表示兩變量存在一定程度的相關。且|r|越接近1,兩變量間線性關系越密切;|r|越接近于0,表示兩變量的線性相關越弱
一般可按三級劃分:|r|<0.4為低度相關;0.4<=|r|<0.7為顯著性相關;0.7<=|r|<1為高度線性相關
API
from scipy.stats import pearsonr -x:array -y:array -Returns:(Pearson`s correlation coefficient,p-value)
代碼演示
from scipy.stats import pearsonr
def p_demo():
# 1.獲取數據
data = pd.read_csv("data.TXT")
print("data:\n", data)
# 2.計算兩個變量之間的相關系數
r=pearsonr(data["one"],data["two"])
print("相關系數:\n", r)
return None如果特征與特征之間相關性很高,通過以下方法處理:
①選取其中一個
②加權求和
③主成分分析
定義
高維數據轉化為低維數據的過程,在此過程中可能會舍棄原有數據、創造新的變量
作用
是數據維數壓縮,盡可能降低原數據維數(復雜度),損失少量信息
應用
回歸分析或者聚類分析當中
API
sklearn.decomposition.PCA(n_components=None)
-將數據分解為較低維數空間
-n_components:
·小數:表示保留百分之多少的信息
·整數:減少到多少特征
-PCA.fit_transform(X)
X:numpy array格式的數據[n_samples,n_features]
-返回值:轉換后指定維度的array
使用
from sklearn.decomposition import PCA
def pca_demo():
data=[[2,8,4,5],[6,3,0,8],[5,4,9,1]]
#1.實例化一個轉換器類
transfer=PCA(n_components=2)
#2.調用fit_transform
result=transfer.fit_transform(data)
print("result:\n",result)
return None“Python中怎么使用sklearn進行特征降維”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。