Python虛擬機中整型的實現原理是什么

這篇文章主要介紹“Python虛擬機中整型的實現原理是什么”的相關知識，小編通過實際案例向大家展示操作過程，操作方法簡單快捷，實用性強，希望這篇“Python虛擬機中整型的實現原理是什么”文章能幫助大家解決問題。

數據結構

在 cpython 內部的 int 類型的實現數據結構如下所示：

typedef struct _longobject PyLongObject;
struct _longobject {
    PyObject_VAR_HEAD
    digit ob_digit[1];
};
#define PyObject_VAR_HEAD      PyVarObject ob_base;
typedef struct {
    PyObject ob_base;
    Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
    _PyObject_HEAD_EXTRA
    Py_ssize_t ob_refcnt;
    struct _typeobject *ob_type;
} PyObject;

上面的數據結構用圖的方式表示出來如下圖所示：

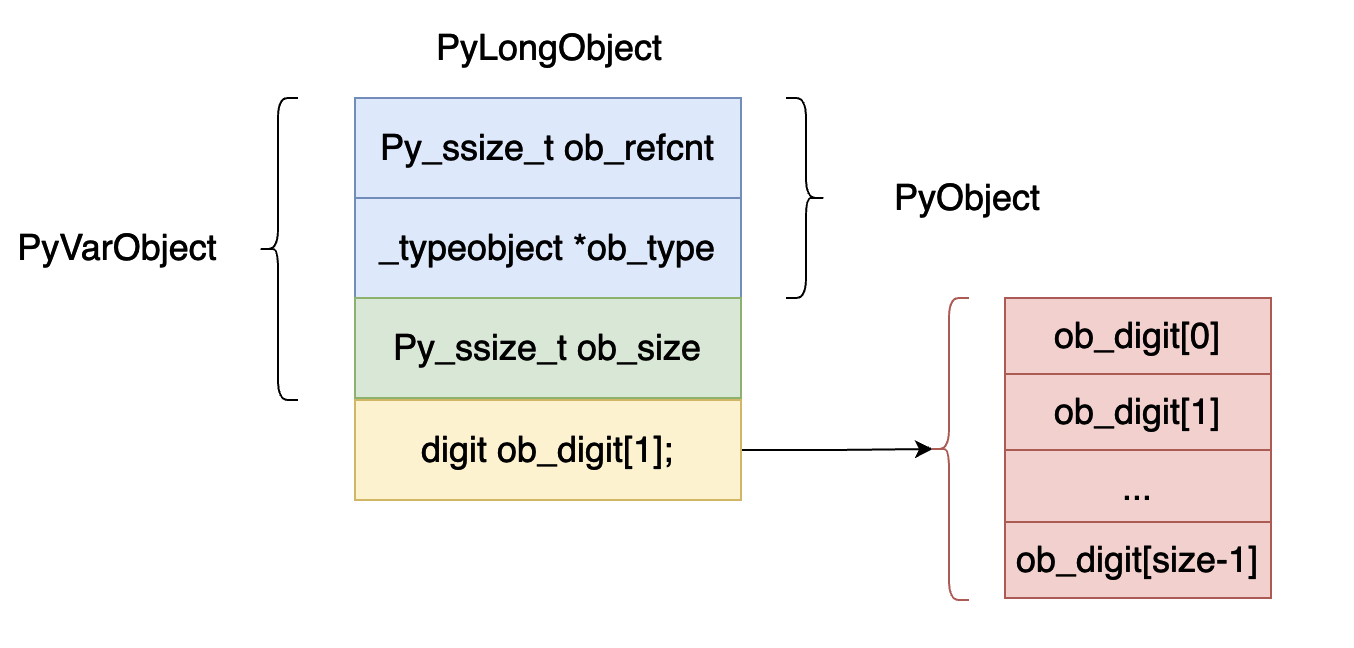
• ob_refcnt，表示對象的引用記數的個數，這個對于垃圾回收很有用處，后面我們分析虛擬機中垃圾回收部分在深入分析。

• ob_type，表示這個對象的數據類型是什么，在 python 當中有時候需要對數據的數據類型進行判斷比如 isinstance, type 這兩個關鍵字就會使用到這個字段。

• ob_size，這個字段表示這個整型對象數組 ob_digit 當中一共有多少個元素。

• digit 類型其實就是 uint32_t 類型的一個 宏定義，表示 32 位的整型數據。

深入分析 PyLongObject 字段的語意

首先我們知道在 python 當中的整數是不會溢出的，這正是 PyLongObject 使用數組的原因。在 cpython 內部的實現當中，整數有 0 、正數、負數，對于這一點在 cpython 當中有以下幾個規定：

• ob_size，保存的是數組的長度，ob_size 大于 0 時保存的是正數，當 ob_size 小于 0 時保存的是負數。

• ob_digit，保存的是整數的絕對值。在前面我們談到了，ob_digit 是一個 32 位的數據，但是在 cpython 內部只會使用其中的前 30 位，這只為了避免溢出的問題。

我們下面使用幾個例子來深入理解一下上面的規則：

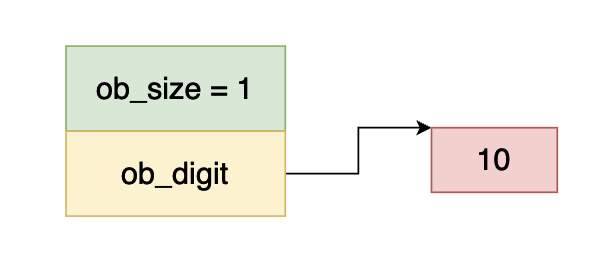
在上圖當中 ob_size 大于 0 ，說明這個數是一個正數，而 ob_digit 指向一個 int32 的數據，數的值等于 10，因此上面這個數表示整數 10 。

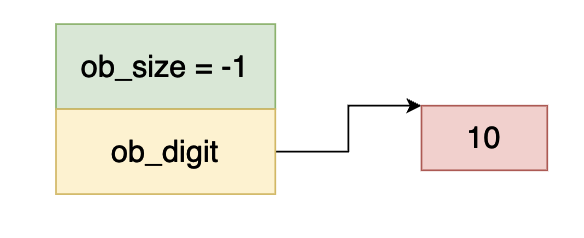
同理 ob_size 小于 0，而 ob_digit 等于 10，因此上圖當中的數據表示 -10 。

上面是一個 ob_digit 數組長度為 2 的例子，上面所表示數據如下所示：

1⋅2⁰+1⋅2¹+1⋅2²+...+1⋅2²⁹+0⋅2³⁰+0⋅2³¹+1⋅2³²

因為對于每一個數組元素來說我們只使用前 30 位，因此到第二個整型數據的時候正好對應著 230，大家可以對應著上面的結果了解整個計算過程。

上面也就很簡單了：

−(1⋅2⁰+1⋅2¹+1⋅2²+...+1⋅2²⁹+0⋅2³⁰+0⋅2³¹+1⋅2³²)

小整數池

為了避免頻繁的創建一些常用的整數，加快程序執行的速度，我們可以將一些常用的整數先緩存起來，如果需要的話就直接將這個數據返回即可。在 cpython 當中相關的代碼如下所示：（小整數池當中緩存數據的區間為[-5, 256]）

#define NSMALLPOSINTS           257
#define NSMALLNEGINTS           5
 
static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];

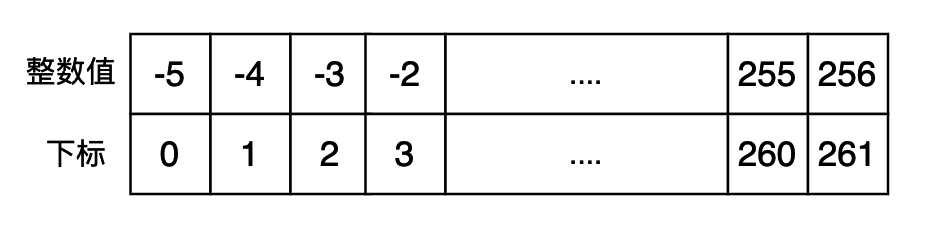
我們使用下面的代碼進行測試，看是否使用了小整數池當中的數據，如果使用的話，對于使用小整數池當中的數據，他們的 id() 返回值是一樣的，id 這個內嵌函數返回的是 python 對象的內存地址。

>>> a = 1
>>> b = 2
>>> c = 1
>>> id(a), id(c)
(4343136496, 4343136496)
>>> a = -6
>>> c = -6
>>> id(a), id(c)
(4346020624, 4346021072)
>>> a = 257
>>> b = 257
>>> id(a), id(c)
(4346021104, 4346021072)
>>>

從上面的結果我們可以看到的是，對于區間[-5, 256]當中的值，id 的返回值確實是一樣的，不在這個區間之內的返回值就是不一樣的。

我們還可以這個特性實現一個小的 trick，就是求一個 PyLongObject 對象所占的內存空間大小，因為我們可以使用 -5 和 256 這兩個數據的內存首地址，然后將這個地址相減就可以得到 261 個 PyLongObject 所占的內存空間大小（注意雖然小整數池當中一共有 262 個數據，但是最后一個數據是內存首地址，并不是尾地址，因此只有 261 個數據），這樣我們就可以求一個 PyLongObject 對象的內存大小。

>>> a = -5
>>> b = 256
>>> (id(b) - id(a)) / 261
32.0
>>>

從上面的輸出結果我們可以看到一個 PyLongObject 對象占 32 個字節。我們可以使用下面的 C 程序查看一個 PyLongObject 真實所占的內存空間大小。

#include "Python.h"
#include <stdio.h>
 
int main()
{
  printf("%ld\n", sizeof(PyLongObject));
  return 0;
}

上面的程序的輸出結果如下所示：

上面兩個結果是相等的，因此也驗證了我們的想法。

從小整數池當中獲取數據的核心代碼如下所示：

static PyObject *
get_small_int(sdigit ival)
{
    PyObject *v;
    assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
    v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
    Py_INCREF(v);
    return v;
}

整數的加法實現

如果你了解過大整數加法就能夠知道，大整數加法的具體實現過程了，在 cpython 內部的實現方式其實也是一樣的，就是不斷的進行加法操作然后進行進位操作。

#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的絕對值
#define PyLong_BASE	((digit)1 << PyLong_SHIFT)
#define PyLong_MASK	((digit)(PyLong_BASE - 1))
 
 
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
    // 首先獲得兩個整型數據的 size 
    Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
    PyLongObject *z;
    Py_ssize_t i;
    digit carry = 0;
    // 確保 a 保存的數據 size 是更大的
    /* Ensure a is the larger of the two: */
    if (size_a < size_b) {
        { PyLongObject *temp = a; a = b; b = temp; }
        { Py_ssize_t size_temp = size_a;
            size_a = size_b;
            size_b = size_temp; }
    }
    // 創建一個新的 PyLongObject 對象，而且數組的長度是 size_a + 1
    z = _PyLong_New(size_a+1);
    if (z == NULL)
        return NULL;
    // 下面就是整個加法操作的核心
    for (i = 0; i < size_b; ++i) {
        carry += a->ob_digit[i] + b->ob_digit[i];
        // 將低 30 位的數據保存下來
        z->ob_digit[i] = carry & PyLong_MASK;
        // 將 carry 右移 30 位，如果上面的加法有進位的話 剛好可以在下一次加法當中使用（注意上面的 carry）
        // 使用的是 += 而不是 =
        carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
    }
    // 將剩下的長度保存 （因為 a 的 size 是比 b 大的）
    for (; i < size_a; ++i) {
        carry += a->ob_digit[i];
        z->ob_digit[i] = carry & PyLong_MASK;
        carry >>= PyLong_SHIFT;
    }
    // 最后保存高位的進位
    z->ob_digit[i] = carry;
    return long_normalize(z); // long_normalize 這個函數的主要功能是保證 ob_size 保存的是真正的數據的長度 因為可以是一個正數加上一個負數 size 還變小了
}
 
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
    PyLongObject *result;
    /* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
       sizeof(digit)*size.  Previous incarnations of this code used
       sizeof(PyVarObject) instead of the offsetof, but this risks being
       incorrect in the presence of padding between the PyVarObject header
       and the digits. */
    if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
        PyErr_SetString(PyExc_OverflowError,
                        "too many digits in integer");
        return NULL;
    }
    // offsetof 會調用 gcc 的一個內嵌函數 __builtin_offsetof 
    // offsetof(PyLongObject, ob_digit)  這個功能是得到 PyLongObject 對象 字段 ob_digit 之前的所有字段所占的內存空間的大小
    result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
                             size*sizeof(digit));
    if (!result) {
        PyErr_NoMemory();
        return NULL;
    }
    // 將對象的 result 的引用計數設置成 1
    return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
 
 
static PyLongObject *
long_normalize(PyLongObject *v)
{
    Py_ssize_t j = Py_ABS(Py_SIZE(v));
    Py_ssize_t i = j;
 
    while (i > 0 && v->ob_digit[i-1] == 0)
        --i;
    if (i != j)
        Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
    return v;
}

關于“Python虛擬機中整型的實現原理是什么”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識，可以關注億速云行業資訊頻道，小編每天都會為大家更新不同的知識點。