您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下Python內建類型int源碼分析的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
問題:對于C語言,下面這個程序運行后的結果是什么?是1000000000000嗎?
#include <stdio.h>
int main(int argc, char *argv[])
{
int value = 1000000;
print("%d\n", value * value)
}輸出如下:
-727379968
在計算機系統中,如果某種類型的變量的存儲空間固定,它能表示的數值范圍就是有限的。以int為例,在C語言中,該類型變量長度為32位,能表示的整數范圍為-2147483648~2147483647。1000000000000顯然是超出范圍的,即發生了整數溢出。但是對于Python中的int,則不會出現這種情況:
>>> 1000000 * 1000000 1000000000000 >>> 10 ** 100 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
int對象的結構體:
typedef struct _longobject PyLongObject;
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};digit數組
#if PYLONG_BITS_IN_DIGIT == 30 typedef uint32_t digit; // ... #elif PYLONG_BITS_IN_DIGIT == 15 typedef unsigned short digit; // ... #endif
digit數組具體用什么整數類型來實現,Python提供了兩個版本,一個是32位的unit32_t,一個是16位的unsigned short,可以通過宏定義指定選用的版本。至于為什么這么設計,這主要是出于內存方面的考量,對于范圍不大的整數,用16位整數表示即可,用32位會比較浪費。
(注:可以看到PYLONG_BITS_IN_DIGIT宏的值為30或15,也就是說Python只使用了30位或15位,這是為什么呢——這是Python出于對加法進位的考量。如果全部32位都用來保存絕對值,那么為了保證加法不溢出(產生進位),需要先強制轉化成64位類型后再進行計算。但犧牲最高1位后,加法運算便不用擔心進位溢出了。那么,為什么對32位時是犧牲最高2位呢?可能是為了和16位整數方案統一起來:如果選用16位整數,Python只使用15位;32位就使用30位。)
實際上,由于PyObject_VAR_HEAD頭部的存在,32位和16位的選擇其實差別不大:
| 整數對象 | 基本單位16位 | 基本單位32位 |
|---|---|---|
| 1 | 24 + 2 * 1 = 26 | 24 + 4 * 1 = 28 |
| 1000000 | 24 + 2 * 2 = 28 | 24 + 4 * 1 = 28 |
| 10000000000 | 24 + 2 * 3 = 30 | 24 + 4 * 2 = 32 |
int對象結構圖示如下:
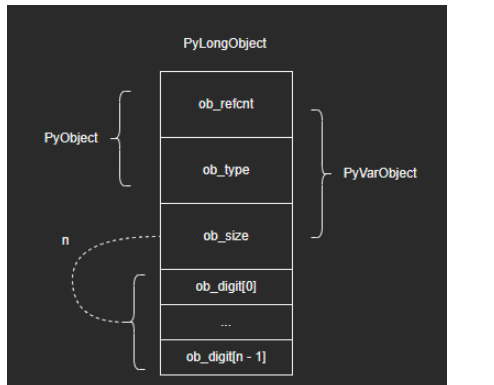
對于比較大的整數,Python將其拆成若干部分,保存在ob_digit數組中。然而我們注意到在結構體定義中,ob_digit數組長度卻固定為1,這是為什么呢?這里資料解釋是:“由于C語言中數組長度不是類型信息,我們可以根據實際需要為ob_digit數組分配足夠的內存,并將其當成長度為n的數組操作。這也是C語言中一個常用的編程技巧。”
但是根據我對C語言的理解,數組是由基址+偏移來確定位置的,初始長度為1的數組,后續如果強行去索引超過這個長度的位置,不是會出問題嗎?不知道是我理解錯了還是什么,這里后續還要進一步考證。
整數分為正數、負數和零,這三種不同整數的存儲方式如下:
將整數的絕對值保存在ob_digit數組中
ob_digit數組長度保存在ob_size字段,若整數為負,則ob_size為負數
整數零的ob_size為0,ob_digit數組為空
下面以五個典型的例子來介紹不同情況下的整數存儲情況:

對于整數0,ob_size = 0,ob_digit為空,無需分配
對于整數10,其絕對值保存在ob_digit數組中,數組長度為1,ob_size字段為1
對于整數-10,其絕對值保存在ob_digit數組中,數組長度為1,ob_size字段為-1
對于整數1073741824(即2^30),由于Python只使用了32位的后30位,所以2^30次方需要兩個數組元素來存儲,整數數組的長度為2。絕對值這樣計算:
2^0 * 0 + 2^30 * 1 = 1073741824
對于整數-4294967297(即-(2^32 + 1)),同樣需要長度為2的數組,但ob_size字段為負數。絕對值這樣計算:
2^0 * 1 + 2^30 * 4 = 4294967297
總結:ob_digit數組存儲數據時,類似230進制計算(或215進制,取決于數組的類型)
問題:通過前面章節的學習,我們知道整數對象是不可變對象,整數運算結果都是以新對象返回的:
>>> a = 1 >>> id(a) 1497146464 >>> a += 1 >>> id(a) 1496146496
Python這樣的設計會帶來一個性能缺陷,程序運行時必定會有大量對象的創建銷毀,即會帶來大量的內存分配和回收消耗,嚴重影響性能。例如對于一個循環100次的for循環,就需要創建100個int對象,這顯然是不能接受的。
對此,Python的解決方法是:預先將常用的整數對象創建好,以后備用,這就是小整數對象池。(和float一樣運用池技術,但是稍有不同,這也是由int和float實際運用的差別導致的)
小整數對象池相關源碼:
#ifndef NSMALLPOSINTS #define NSMALLPOSINTS 257 #endif #ifndef NSMALLNEGINTS #define NSMALLNEGINTS 5 #endif static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];
NSMALLPOSINTS宏規定了對象池正數個數(包括0),默認257個NSMALLNEGINTS宏規定了對象池負數個數,默認為5個small_ints是一個整數對象數組,保存預先創建好的小整數對象
以默認配置為例,Python啟動后靜態創建一個包含262個元素的整數數組,并依次初始化-5到-1,0,和1到256這些整數對象。小整數對象池結構如下:

示例1:
>>> a = 1 + 0 >>> b = 1 * 1 >>> id(a), id(b) (1541936120048, 1541936120048)
由于1 + 0的計算結果為1,在小整數范圍內,Python會直接從靜態對象池中取出整數1;1 * 1也是同理。名字a和b其實都跟一個對象綁定(有關名字綁定的內容可以看這篇博客:Python源碼學習筆記:Python作用域與名字空間),即小整數對象池中的整數1,因此它們的id相同。
示例2:
>>> c = 1000 + 0 >>> d = 1000 * 1 >>> id(c), id(d) (3085872130224, 3085872130256)
1000 + 0 和1000 * 1的計算結果都是1000,但由于1000不在小整數池范圍內,Python會分別創建對象并返回,因此c和d綁定的對象id也就不同了。
注:這里大家如果使用Pycharm來運行的話就會發現它們的id是一樣的:
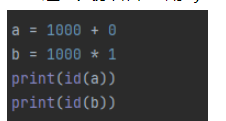
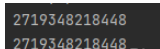
這里的原因本質上是和字節碼相關的,在IDLE中,每個命令都會單獨去編譯,而在Pycharm中是編譯整個py文件,在同一上下文。
問題:在之前我們了解到了整數對象的內部結構,對于Python如何應對“整數溢出”這個問題有了一個初步的認識。但是真正的難點在于大整數數學運算的實現。
整數對象的運算由整數類型對象中的tp_as_number、tp_as_sequence、tp_as_mapping這三個字段所決定。整數類型對象PyLong_Type源碼如下:(只列出部分字段)
PyTypeObject PyLong_Type = {
PyVarObject_HEAD_INIT(&PyType_Type, 0)
"int", /* tp_name */
offsetof(PyLongObject, ob_digit), /* tp_basicsize */
sizeof(digit), /* tp_itemsize */
// ...
&long_as_number, /* tp_as_number */
0, /* tp_as_sequence */
0, /* tp_as_mapping */
// ...
};整數對象僅支持數值型操作long_as_number:
static PyNumberMethods long_as_number = {
(binaryfunc)long_add, /*nb_add*/
(binaryfunc)long_sub, /*nb_subtract*/
(binaryfunc)long_mul, /*nb_multiply*/
long_mod, /*nb_remainder*/
long_divmod, /*nb_divmod*/
long_pow, /*nb_power*/
(unaryfunc)long_neg, /*nb_negative*/
(unaryfunc)long_long, /*tp_positive*/
(unaryfunc)long_abs, /*tp_absolute*/
(inquiry)long_bool, /*tp_bool*/
(unaryfunc)long_invert, /*nb_invert*/
long_lshift, /*nb_lshift*/
(binaryfunc)long_rshift, /*nb_rshift*/
long_and, /*nb_and*/
long_xor, /*nb_xor*/
long_or, /*nb_or*/
long_long, /*nb_int*/
0, /*nb_reserved*/
long_float, /*nb_float*/
0, /* nb_inplace_add */
0, /* nb_inplace_subtract */
0, /* nb_inplace_multiply */
0, /* nb_inplace_remainder */
0, /* nb_inplace_power */
0, /* nb_inplace_lshift */
0, /* nb_inplace_rshift */
0, /* nb_inplace_and */
0, /* nb_inplace_xor */
0, /* nb_inplace_or */
long_div, /* nb_floor_divide */
long_true_divide, /* nb_true_divide */
0, /* nb_inplace_floor_divide */
0, /* nb_inplace_true_divide */
long_long, /* nb_index */
};至此,我們明確了整數對象支持的全部數學運算,以及對應的處理函數:(只列出部分函數)
| 數學運算 | 處理函數 | 示例 |
|---|---|---|
| 加法 | long_add | a + b |
| 減法 | long_sub | a - b |
| 乘法 | long_mul | a * b |
| 取模 | long_mod | a % b |
| 除法 | long_divmod | a / b |
| 指數 | long_pow | a ** b |
整數對象、整數類型對象以及整數數學運算處理函數之間的關系:
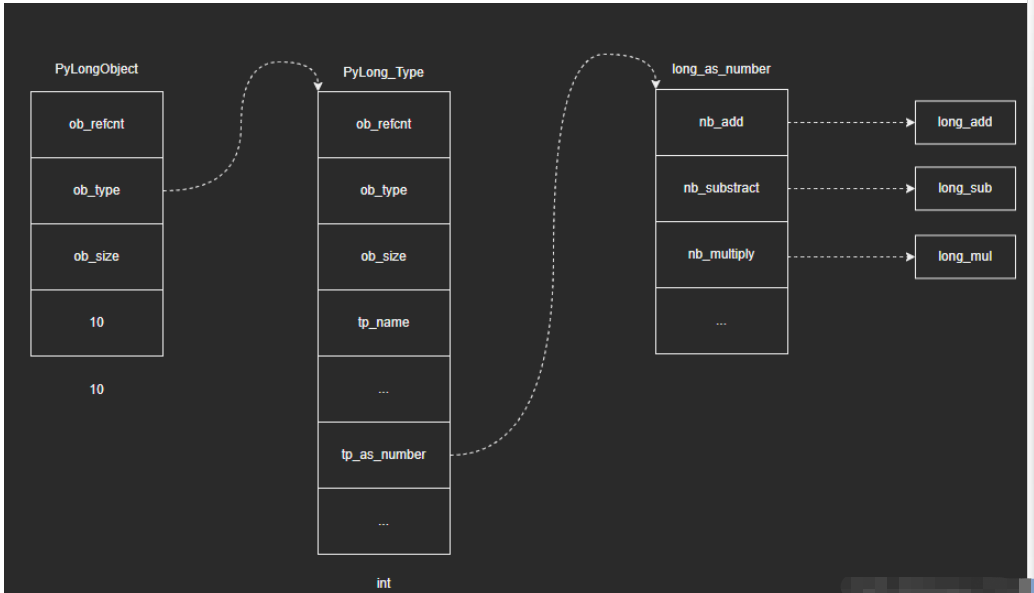
以加法為例,來認識大整數運算的處理過程。
加法處理函數long_add()
static PyObject *
long_add(PyLongObject *a, PyLongObject *b)
{
PyLongObject *z;
CHECK_BINOP(a, b);
if (Py_ABS(Py_SIZE(a)) <= 1 && Py_ABS(Py_SIZE(b)) <= 1) {
return PyLong_FromLong(MEDIUM_VALUE(a) + MEDIUM_VALUE(b));
}
if (Py_SIZE(a) < 0) {
if (Py_SIZE(b) < 0) {
z = x_add(a, b);
if (z != NULL) {
/* x_add received at least one multiple-digit int,
and thus z must be a multiple-digit int.
That also means z is not an element of
small_ints, so negating it in-place is safe. */
assert(Py_REFCNT(z) == 1);
Py_SIZE(z) = -(Py_SIZE(z));
}
}
else
z = x_sub(b, a);
}
else {
if (Py_SIZE(b) < 0)
z = x_sub(a, b);
else
z = x_add(a, b);
}
return (PyObject *)z;
}主體邏輯如下:
第4行:定義變量z用于臨時保存計算結果
第8~10行:如果兩個對象數組長度均不超過1,用MEDIUM_VALUE宏將其轉化成C整數進行運算(這種優化也是可以學習的)
第13~17行:如果兩個整數均為負數,調用x_add計算兩者絕對值之和,再將結果符號設置為負(16行處)
第20行:如果a為負數,b為正數,調用x_sub計算b和a的絕對值之差即為最終結果
第24行:如果a為正數,b為負數,調用x_sub計算a和b的絕對值之差即為最終結果
第26行:如果兩個整數均為正數,調用x_add計算兩個絕對值之和即為最終結果
因此,long_add函數實際上將整數加法轉化成了絕對值加法x_add和絕對值減法x_sub,以及MEDIUM_VALUE。絕對值加法和絕對值減法不用考慮符號對計算結果的影響,實現較為簡單,這是Python將整數運算轉化成絕對值運算的原因。(這里也可以學習下)
大整數運算涉及到兩個數組之間的加法,整數數值越大,整數對象底層數組就越長,運算開銷也會越大。但是運算處理函數提供了一個快速通道:如果參與運算的整數對象底層數組長度均不超過1,直接將整數對象轉化成C整數類型進行運算,性能耗損極小。滿足這個條件的整數范圍在-1073741823~1073747823之間,足以覆蓋大部分運算情況了。
下面我們來看一下Python是如何對數組進行加法運算的。x_add()源碼:
/* Add the absolute values of two integers. */
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
z->ob_digit[i] = carry;
return long_normalize(z);
}源碼分析:
第10~15行:如果a數組長度比較小,將a、b交換,數組長度較大的那個在前面(感覺做算法題有時候就需要交換下,方便統一處理)
第16~18行:創建新整數對象,用于保存計算結果(注意到長度必須要比a大,因為可能要進位)
第19~23行:遍歷b底層數組,與a對應部分相機啊并保存在z中,需要注意到進位(可以看到這里是用按位與和右移進行計算的,通過位于算來處理也是很高效的,算法題中也比較常見)
第24~28行:遍歷a底層數組的剩余部分,與進位相加后保存在z中,同樣要注意進位運算
第29行:將進位寫入z底層數組最高位單元中
第30行:標準化z,去除計算結果z底層數組中前面多余的0
至此,我們對int和float有了一定的認識,也自然會有一個問題:將大整數int轉化為float時發生溢出怎么辦?
示例:
>>>i = 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 >>> f = float(i) Traceback (most recent call last): File "<pyshell#1>", line 1, in <module> f = float(i) OverflowError: int too large to convert to float
由于float是有長度限制的,它的大小也是有上限的,因此當我們將一個很大的int轉化為float時,如果超出上限就會報錯。對此我們可以使用Decimal來解決:(這里只介紹了使用方式,具體原理大家可以去了解一下)
>>> from decimal import Decimal >>>d = Decimal(i) >>>f2 = float(d) >>> f2 inf
可以看到將i通過Decimal()轉化后就不會報錯了。
以上就是“Python內建類型int源碼分析”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。