您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要為大家展示了“Python/R語言如何分別實現斐波那契數列”,內容簡而易懂,條理清晰,希望能夠幫助大家解決疑惑,下面讓小編帶領大家一起研究并學習一下“Python/R語言如何分別實現斐波那契數列”這篇文章吧。
有 5 個人坐在一起,問第五個?人多少歲?他說比第 4 個人大 2 歲。問第 4 個 人歲數,他說比第 3 個人大 2 歲。問第三個人,又說比第 2 人大兩歲。問第 2 個人,說比第一個人大兩歲。最后問第一個人,他說是 10 歲。請問第五個人多 大?
這個問題簡化之后便是求一個等比數列的第 5 項是多少!
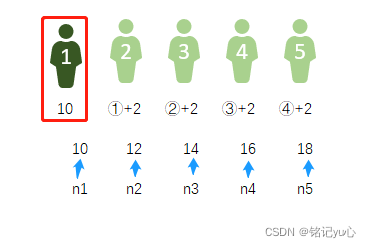
根據數學思維即可得出該數列為 1 組等差數列:
an=2(n−1)+10
既然問題已經提取到這兒了,那接下來就只剩如何用代碼實現了:
1.2.1 Python實現代碼
def age():
#互動界面——輸入查詢的第幾個
n = int(input("請問你需要第幾個人年齡:"))
no_1 = 10
if n<0:
print("請輸入大于0的數值!!!")
else:
#主要計算數列
no_n = (n-1)*2+no_1
return n,no_n
print("第{}個人的年齡是:{}歲。".format(*age()))
1.2.1 R語言實現代碼
caixiang <- function(){
one_age <-as.integer(readline('請輸入第一個人的年齡:'))
n <- as.integer(readline("請輸入查詢的第幾個人:"))
n_age <<- one_age + 2*(n-1)
return(n_age)
}
test_1 <- function(){
caixiang()
cat("查詢的年齡為:",n_age)
}
test_1()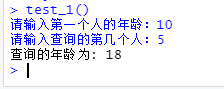
這個實驗的代碼部分并不難,僅需要輸入數學公式即可。
代碼部分均使用函數的形式進行包裝方便理解;函數內部采用互動的方式,便于拓展使用。
斐波那契數列(Fibonacci sequence),又稱黃金分割數列,因數學家萊昂納多·斐波那契(Leonardo Fibonacci)以兔子繁殖為例子而引入,故又稱為“兔子數列”,指的是這樣一個數列:1、1、2、3、5、8、13、21、34、……
在數學上,斐波那契數列以如下被以遞推的方法定義:
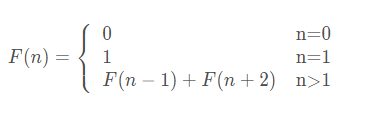
現代物理、準晶體結構、化學等領域,斐波納契數列都有直接的應用。在數學中更是應用廣泛,各種推理推論在這就不展開了,畢竟還是以代碼生成斐波那契數列為主。
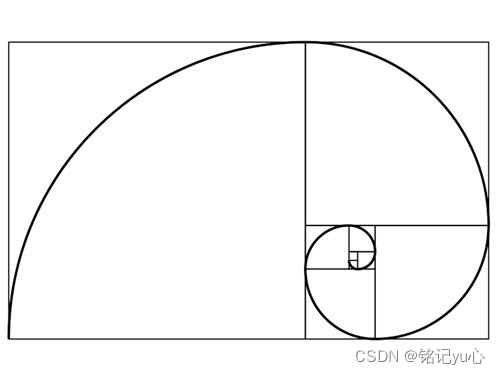
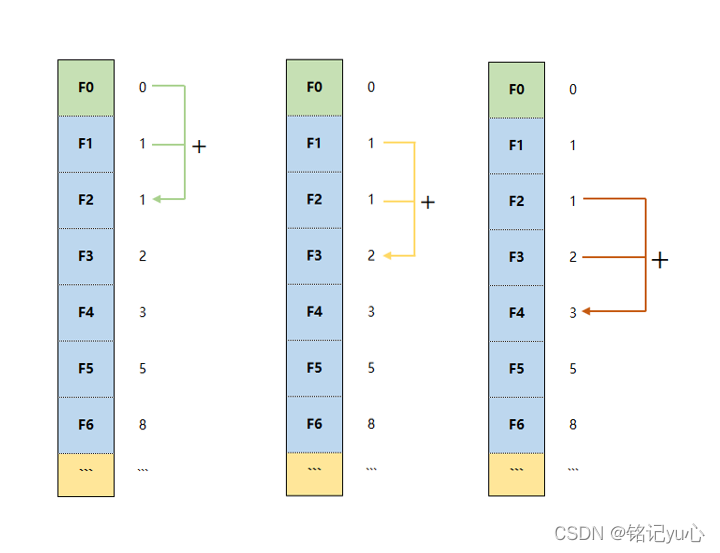
根據數列的通項式可得出如圖的加法;顯然這是種向下的循環加法。則定以for循環對該數列每一個值的單獨輸出。
2.2.1 Python代碼實現
def fib(n):
a,b = 1,1
# 循環打印
for i in range(n):
print(a,end = " ")
temp = a
a = b
b = temp + b
num = int(input("請輸入需要打印的斐波那數列的數據個數(從 1 開始):"))
fib(num)
2.2.2 R語言代碼實現
fib <- function(n){
n <- as.integer(
readline("請輸入需要打印的斐波那數列的數據個數(從 1 開始):"))
a = b = 1
for (i in 1:n) {
print(a,end = " ")
temp <- a
a <- b
b <- a + temp
}
}
test_2 <- function(){
cat("斐波那契數列為:")
fib(n)
}
test_2()
在圖解之后,這個數列的輸出已經不再困難,均是使用 for 循環加上 temp 指針的方式。這里不展開介紹指針的移動規則,如有需要留言就可。然而在每次循環時將得出的值進行輸出就能不被覆蓋。
代碼部分均使用函數的形式進行包裝方便理解;函數內部采用互動的方式,便于拓展使用。
以上是“Python/R語言如何分別實現斐波那契數列”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。