您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“Python中交叉驗證的方法有哪些”的相關知識,小編通過實際案例向大家展示操作過程,操作方法簡單快捷,實用性強,希望這篇“Python中交叉驗證的方法有哪些”文章能幫助大家解決問題。
交叉驗證是一種用于估計機器學習模型性能的統計方法,它是一種評估統計分析結果如何推廣到獨立數據集的方法。
在交叉驗證中,我們將訓練數據生成多個小的訓練測試分割,使用這些拆分來調整您的模型。 例如,在標準的 k 折交叉驗證中,我們將數據劃分為 k 個子集。 然后,我們在 k-1 個子集上迭代訓練算法,同時使用剩余的子集作為測試集。 通過這種方式,我們可以在未參與訓練的數據上測試我們的模型。
在本文中,我將分享 7 種最常用的交叉驗證技術及其優缺點,我還提供了每種技術的代碼片段。
下面列出了這些技術方法:
HoldOut 交叉驗證
K-Fold 交叉驗證
分層 K-Fold交叉驗證
Leave P Out 交叉驗證
留一交叉驗證
蒙特卡洛 (Shuffle-Split)
時間序列(滾動交叉驗證)
在這種交叉驗證技術中,整個數據集被隨機劃分為訓練集和驗證集。 根據經驗,整個數據集的近 70% 用作訓練集,其余 30% 用作驗證集。

優點:
1.快速執行:因為我們必須將數據集拆分為訓練集和驗證集一次,并且模型將在訓練集上僅構建一次,因此可以快速執行。
缺點:
不適合不平衡數據集:假設我們有一個不平衡數據集,它具有“0”類和“1”類。 假設 80% 的數據屬于“0”類,其余 20% 的數據屬于“1”類。在訓練集大小為 80%,測試數據大小為數據集的 20% 的情況下進行訓練-測試分割。 可能會發生“0”類的所有 80% 數據都在訓練集中,而“1”類的所有數據都在測試集中。 所以我們的模型不能很好地概括我們的測試數據,因為它之前沒有看到過“1”類的數據。
大量數據無法訓練模型。
在小數據集的情況下,將保留一部分用于測試模型,其中可能具有我們的模型可能會錯過的重要特征,因為它沒有對該數據進行訓練。
代碼片段
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
iris=load_iris()
X=iris.data
Y=iris.target
print("Size of Dataset {}".format(len(X)))
logreg=LogisticRegression()
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.3,random_state=42)
logreg.fit(x_train,y_train)
predict=logreg.predict(x_test)
print("Accuracy score on training set is {}".format(accuracy_score(logreg.predict(x_train),y_train)))
print("Accuracy score on test set is {}".format(accuracy_score(predict,y_test)))
在這種 K 折交叉驗證技術中,整個數據集被劃分為 K 個相等大小的部分。 每個分區稱為一個“折疊”。因此,因為我們有 K 個部分,所以我們稱之為 K 折疊。 一折用作驗證集,其余 K-1 折用作訓練集。
該技術重復 K 次,直到每個折疊用作驗證集,其余折疊用作訓練集。
模型的最終精度是通過取k-models 驗證數據的平均精度來計算的。

優點:
整個數據集既用作訓練集又用作驗證集:
缺點:
不用于不平衡的數據集:正如在 HoldOut 交叉驗證的情況下所討論的,在 K-Fold 驗證的情況下也可能發生訓練集的所有樣本都沒有樣本形式類“1”,并且只有 類“0”。驗證集將有一個類“1”的樣本。
不適合時間序列數據:對于時間序列數據,樣本的順序很重要。 但是在 K 折交叉驗證中,樣本是按隨機順序選擇的。
代碼片段:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,KFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
kf=KFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=kf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))
分層 K-Fold 是 K-Fold 交叉驗證的增強版本,主要用于不平衡的數據集。 就像 K-fold 一樣,整個數據集被分成大小相等的 K-fold。
但是在這種技術中,每個折疊將具有與整個數據集中相同的目標變量實例比率。
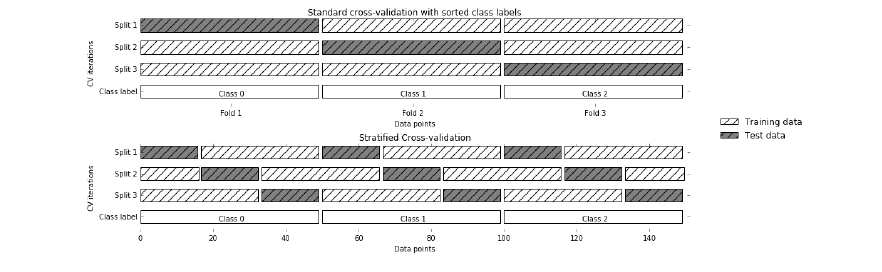
優點:
對于不平衡數據非常有效:分層交叉驗證中的每個折疊都會以與整個數據集中相同的比率表示所有類別的數據。
缺點:
不適合時間序列數據:對于時間序列數據,樣本的順序很重要。 但在分層交叉驗證中,樣本是按隨機順序選擇的。
代碼片段:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,StratifiedKFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
stratifiedkf=StratifiedKFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=stratifiedkf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))
Leave P Out 交叉驗證是一種詳盡的交叉驗證技術,其中 p 樣本用作驗證集,剩余的 np 樣本用作訓練集。
假設我們在數據集中有 100 個樣本。 如果我們使用 p=10,那么在每次迭代中,10 個值將用作驗證集,其余 90 個樣本將用作訓練集。
重復這個過程,直到整個數據集在 p-樣本和 n-p 訓練樣本的驗證集上被劃分。
優點:
所有數據樣本都用作訓練和驗證樣本。
缺點:
計算時間長:由于上述技術會不斷重復,直到所有樣本都用作驗證集,因此計算時間會更長。
不適合不平衡數據集:與 K 折交叉驗證相同,如果在訓練集中我們只有 1 個類的樣本,那么我們的模型將無法推廣到驗證集。
代碼片段
from sklearn.model_selection import LeavePOut,cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
iris=load_iris()
X=iris.data
Y=iris.target
lpo=LeavePOut(p=2)
lpo.get_n_splits(X)
tree=RandomForestClassifier(n_estimators=10,max_depth=5,n_jobs=-1)
score=cross_val_score(tree,X,Y,cv=lpo)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))
留一交叉驗證是一種詳盡的交叉驗證技術,其中 1 個樣本點用作驗證集,其余 n-1 個樣本用作訓練集。
假設我們在數據集中有 100 個樣本。 然后在每次迭代中,1 個值將用作驗證集,其余 99 個樣本作為訓練集。 因此,重復該過程,直到數據集的每個樣本都用作驗證點。
它與使用 p=1 的 LeavePOut 交叉驗證相同。
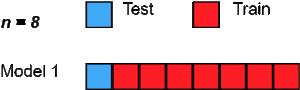
代碼片段:
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import LeaveOneOut,cross_val_score
iris=load_iris()
X=iris.data
Y=iris.target
loo=LeaveOneOut()
tree=RandomForestClassifier(n_estimators=10,max_depth=5,n_jobs=-1)
score=cross_val_score(tree,X,Y,cv=loo)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))
蒙特卡羅交叉驗證,也稱為Shuffle Split交叉驗證,是一種非常靈活的交叉驗證策略。 在這種技術中,數據集被隨機劃分為訓練集和驗證集。
我們已經決定了要用作訓練集的數據集的百分比和用作驗證集的百分比。 如果訓練集和驗證集大小的增加百分比總和不是 100,則剩余的數據集不會用于訓練集或驗證集。
假設我們有 100 個樣本,其中 60% 的樣本用作訓練集,20% 的樣本用作驗證集,那么剩下的 20%( 100-(60+20)) 將不被使用。
這種拆分將重復我們必須指定的“n”次。

優點:
1.我們可以自由使用訓練和驗證集的大小。
2.我們可以選擇重復的次數,而不依賴于重復的折疊次數。
缺點:
可能不會為訓練集或驗證集選擇很少的樣本。
不適合不平衡的數據集:在我們定義了訓練集和驗證集的大小后,所有的樣本都是隨機選擇的,所以訓練集可能沒有測試中的數據類別 設置,并且該模型將無法概括為看不見的數據。
代碼片段:
from sklearn.model_selection import ShuffleSplit,cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
logreg=LogisticRegression()
shuffle_split=ShuffleSplit(test_size=0.3,train_size=0.5,n_splits=10)
scores=cross_val_score(logreg,iris.data,iris.target,cv=shuffle_split)
print("cross Validation scores:n {}".format(scores))
print("Average Cross Validation score :{}".format(scores.mean()))
什么是時間序列數據?
時間序列數據是在不同時間點收集的數據。由于數據點是在相鄰時間段收集的,因此觀測值之間可能存在相關性。這是區分時間序列數據與橫截面數據的特征之一。
在時間序列數據的情況下如何進行交叉驗證?
在時間序列數據的情況下,我們不能選擇隨機樣本并將它們分配給訓練集或驗證集,因為使用未來數據中的值來預測過去數據的值是沒有意義的。
由于數據的順序對于時間序列相關問題非常重要,所以我們根據時間將數據拆分為訓練集和驗證集,也稱為“前向鏈”方法或滾動交叉驗證。
我們從一小部分數據作為訓練集開始。基于該集合,我們預測稍后的數據點,然后檢查準確性。
然后將預測樣本作為下一個訓練數據集的一部分包括在內,并對后續樣本進行預測。

優點:
最好的技術之一。
缺點:
不適用于其他數據類型的驗證:與其他技術一樣,我們選擇隨機樣本作為訓練或驗證集,但在該技術中數據的順序非常重要。
代碼片段:
import numpy as np
from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])
time_series = TimeSeriesSplit()
print(time_series)
for train_index, test_index in time_series.split(X):
print("TRAIN:", train_index, "TEST:", test_index)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]關于“Python中交叉驗證的方法有哪些”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識,可以關注億速云行業資訊頻道,小編每天都會為大家更新不同的知識點。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。