您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這期內容當中小編將會給大家帶來有關python如何繪制超炫酷動態Julia集,文章內容豐富且以專業的角度為大家分析和敘述,閱讀完這篇文章希望大家可以有所收獲。
此Julia非彼Julia,指的是對于某復數 c c c,使得迭代式 f ( z ) = z 2 + c f(z)=z^2+c f(z)=z2+c收斂的復數 z z z的集合。例如,當 c = 0 c=0 c=0時,那么其收斂區間為 z 2 < 1 z^2<1 z2<1的單位圓,對應的 c c c的Julia集便是 cos ? θ + i sin ? θ \cos\theta+i\sin\theta cosθ+isinθ。
特別地,當 c = z c=z c=z的初始值時,符合收斂條件的 z z z的便構成大名鼎鼎的Mandelbrot集
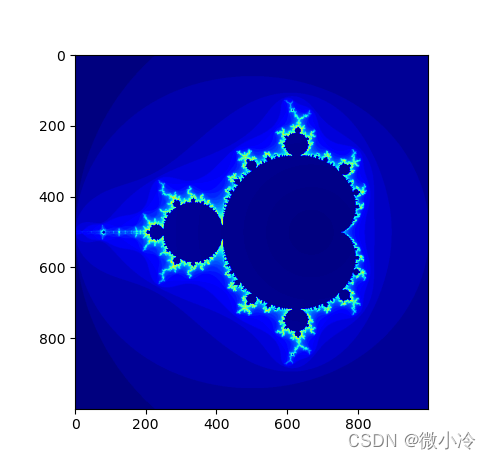
在上圖中,顏色表示該點的發散速度,可以理解為開始發散時迭代的次數。其生成代碼也非常簡單,唯一需要注意的是,由于使用了大量的矩陣運算,故使用了cupy,如果電腦沒裝cuda,只需將所有的cp改為np即可。
# 這些代碼會在后面的程序中反復調用,不再說明
import numpy as np
import time
import matplotlib.pyplot as plt
import cupy as cp
#生成z坐標 x0,y0 為起始點, nx,ny為點數, delta為點距
def genZ(x0, y0, nx, ny, delta):
real, img = cp.indices([nx,ny])*delta
real += x0
img += y0
return real.T+img.T*1j
#獲取Julia集,n為迭代次數,m為判定發散點,大于1即可
def getJulia(z,c,n,m=2):
t = time.time()
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
for i in range(n):
absz = cp.abs(z)
z[absz>m]=0 #對開始發散的點置零
c[absz>m]=0
out[absz>m]=i #記錄發散點的發散速度
z = z*z + c
print("time:",time.time()-t)
return out
z1 = genZ(-2,-1.5,1000,1000,0.003)
mBrot = getJulia(z1,z1,50)
plt.imshow(mBrot.get(), cmap=plt.cm.jet)
plt.show()如果對其生成過程感興趣,那么可以觀察一下隨著迭代次數的增加,圖像的變化情況
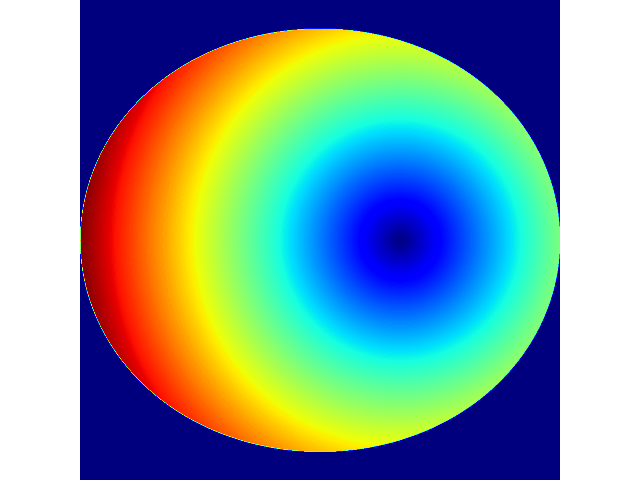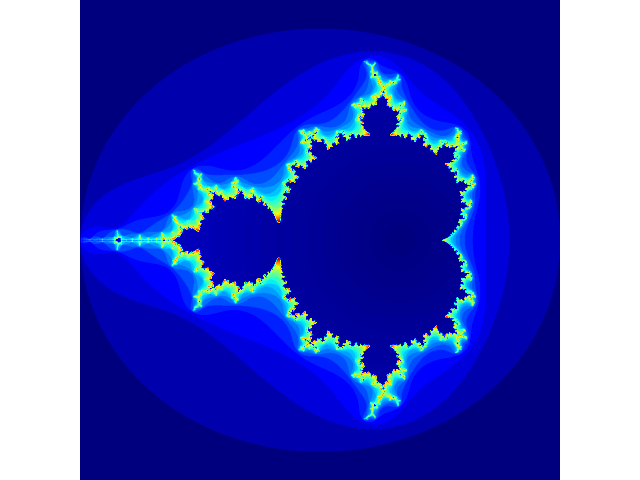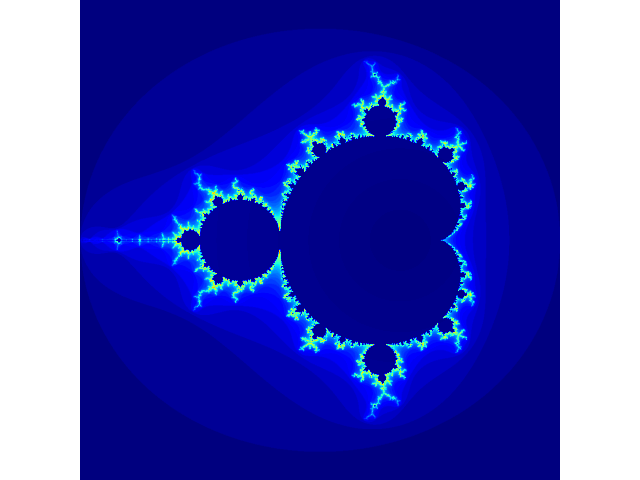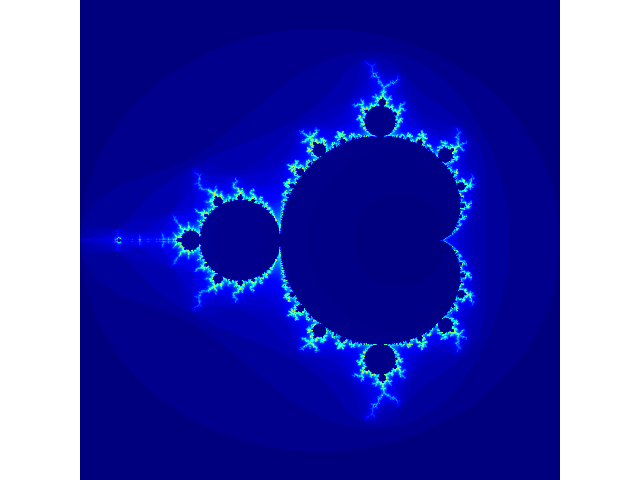
代碼如下。
from matplotlib import animation
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
def getJulias(z,c,n,m=2):
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
J = []
for i in range(n):
z = z*z + c
absz = cp.abs(z)
z[absz>m]=0 #對開始發散的點置零
c[absz>m]=0
out[absz>m]=i #記錄發散點的發散速度
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
J.append([im])
return J
N = 75 #迭代次數
z1 = genZ(-2,-1.5,1000,1000,0.003)
J = getJulias(z1,z1,N)
ani = animation.ArtistAnimation(fig, J, interval=50, blit=True,repeat_delay=1000)
plt.show()
ani.save('julias.gif',writer='imagemagick')Mandelbrot集的分形特征意味著我們所生成的圖片可以無限放大,但是受到柵格化尺寸的影響,手動的放大并不會更改其真實尺寸,
為了照顧觀感,將縮放中心作為圖像的中心,所以對genZ函數進行修改。如果選取(-0.75,-0.2)作為縮放中心,則其變化如下

代碼為
from matplotlib import animation
# 生成z坐標 xy=np.array([xc,yc]) 為起始點,
# nxy=np.array([nx,ny])為點數, delta為點距
def genZbyCenter(xy,nxy,delta):
x0, y0 = xy-np.array(nxy)*delta/2
return genZ(x0,y0,*nxy,delta)
mBrots = []
xy = [-0.75,-0.2]
nxy = [1000,1000]
delta0 = 0.003 #初始寬度
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
for n in range(50):
z1 = genZbyCenter(xy,nxy,1.1**(-n)*delta0)
out = getJulia(z1,z1,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50, blit=True)
plt.show()
ani.save('zoom.gif',writer='imagemagick')如果更改c的值,那么就能得到一個變化著的Julia集,例如,下面選取一條直線
y = x y=x y=x
上面的Julia集,效果如圖所示

代碼為
z1 = genZ(-2,-1.5,1000,1000,0.003)
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
mBrots = []
for x in np.arange(0.5,1,0.01):
c = x + x*1j
out = getJulia(z1,c,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50)
plt.show()
ani.save('julia.gif',writer='imagemagick')上述就是小編為大家分享的python如何繪制超炫酷動態Julia集了,如果剛好有類似的疑惑,不妨參照上述分析進行理解。如果想知道更多相關知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。