您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“C語言經典案例青蛙跳臺階和漢諾塔問題怎么實現”,在日常操作中,相信很多人在C語言經典案例青蛙跳臺階和漢諾塔問題怎么實現問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”C語言經典案例青蛙跳臺階和漢諾塔問題怎么實現”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
一、青蛙跳臺階
題目
思路
分析
1. 從跳法次數分析
2. 從過程分析
二、青蛙跳臺階變式1
題目
分析
三、青蛙跳臺階變式2
題目
分析
四、漢諾塔問題(求步數)
題目
思路
分析
五、漢諾塔問題(求移動過程)
題目
思路
分析
一只青蛙一次可以跳上1級臺階,也可以跳上2級臺階。求該青蛙跳上一個 n 級的臺階總共有多少種跳法
遇見題目我們可以在紙上先動手畫畫,把最簡單的幾種方式列出來,作比較,找規律。
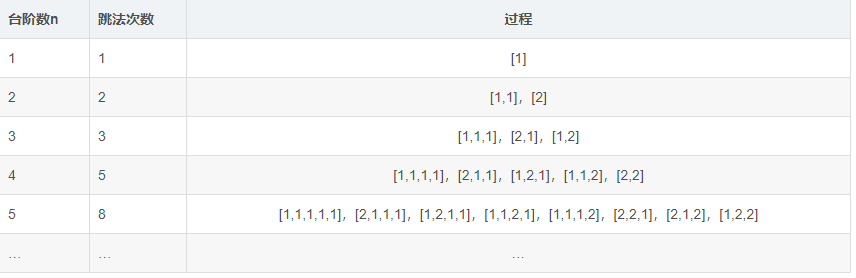
按照上面表格可以從跳法次數,過程,或者兩者結合找規律
觀察表格,可以知道從n>=3時,第n個數就是前兩個數的和(與斐波那契數列一樣)
我們自己推論,當臺階數為n時,設跳法有f(n)次,如果青蛙先跳1階,則剩下的臺階數為n-1,即剩余跳法有f(n-1)次;如果青蛙先跳2階,則剩下的臺階數為n-2,即剩余跳法有f(n-2)次。
故跳法次數f(n)=f(n-1)+f(n-2),因為等號右邊有兩個值,故當n=1,n=2時為最后的特殊限制條件
下面代碼為遞歸求法,如果想用非遞歸,可以將遞歸通項改成循環
代碼1(遞歸)
#include <stdio.h>
int jump(int n)
{
if (n == 1)
return 1;
if (n == 2)
return 2;
return jump(n - 1) + jump(n - 2);
}
int main()
{
int n;
scanf("%d", &n);
int ret = jump(n);
printf("%d", ret);
return 0;
}
觀察表格,可以知道,跳n階臺階,跳兩階臺階次數可以為0到n/2次,而每一次跳兩階臺階的順序也是不定的。可以通過計數原理的組合數C(n,m),表示從n個數中選m個數排列。n表示每次需要跳的次數,m表示一次跳兩階的次數
組合數C(n,m),可以由n!/(m!*(n-m)!)求得
下面代碼為非遞歸求法,如果想要寫成遞歸,可以根據循環修改
代碼2(非遞歸)
#include <stdio.h>
int fac(int m)
{
int i = 0;
int count = 1;
for (i = 1; i <= m; i++)
{
count *= i;
}
return count;
}
int jump(int n)
{
int i = 0; //i為跳兩階臺階的次數
int sum = 0; //sum為計算跳法
for (i = 0; i <= n / 2; i++)
{
int a = 0;
a = n - i * 2 + i; //a為跳到n階臺階跳的次數
sum += fac(a) / (fac(i)*fac(a - i));
}
return sum;
}
int main()
{
int n;
scanf("%d", &n);
int ret = jump(n);
printf("%d", ret);
return 0;
}一只青蛙一次可以跳上1級臺階,也可以跳上2級臺階…也可以跳n級臺階。求該青蛙跳上一個 n 級的臺階總共有多少種跳法
根據原題推論,當臺階數為n時,設跳法有f(n)次,如果青蛙先跳1階,則剩下的臺階數為n-1,即剩余跳法有f(n-1)次;如果青蛙先跳2階,則剩下的臺階數為n-2,即剩余跳法有f(n-2)次。
那么當青蛙跳3階臺階,則剩下的臺階數為n-3,即剩余跳法有f(n-3)次…當青蛙跳n階臺階,則剩下的臺階數為n-n,即剩余跳法有f(n-n)次
故跳法次數f(n)=f(n-1)+f(n-2)+f(n-3)…+f(n-n)
由推論可得f(n-1)=f(n-2)+f(n-3)…+f(n-n),將其代入上面式子
故跳法次數為f(n)=2*f(n-1),因為等號右邊只有一個值,故n=1為最后的特殊限制條件
代碼3(遞歸)
#include <stdio.h>
int jump(int n)
{
if (n == 1)
return 1;
return 2*jump(n - 1);
}
int main()
{
int n;
scanf("%d", &n);
int ret = jump(n);
printf("%d", ret);
return 0;
}一只青蛙一次可以跳上1級臺階,也可以跳上2級臺階…也可以跳m級臺階。求該青蛙跳上一個 n 級的臺階總共有多少種跳法(m<=n)
根據變式1推論得f(n)=f(n-1)+f(n-2)+f(n-3)…+f(n-n)
而這里最多一次只能跳m階,故f(n)=f(n-1)+f(n-2)+f(n-3)…+f(n-m)
由推論得f(n-1)=f(n-2)+f(n-3)…+f(n-m)+f(n-m-1),代入上面式子
故跳法次數為f(n)=2*f(n-1)-f(n-m-1)
因為通過遞歸n的值在減少,當n<m時,其實最多就只能跳n階,與變式1就是一樣的問題了
代碼4(遞歸)
#include <stdio.h>
int jump(int n,int m)
{
if (n > m)
return 2 * jump(n - 1, m) - jump(n - 1 - m, m);
else
{
if (n == 1)
return 1;
return 2 * jump(n - 1, n);
}
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
int ret = jump(n,m);
printf("%d", ret);
return 0;
}有A,B,C三個柱子,A柱子上從上到下,從小到大排列著n個圓盤。現要求將A柱子上的n個圓盤全部移動到C柱子上,依然按照從上到下,從小到大的順序排列。且對移動過程要求如下:
a)一次只能移動一個盤子。
b)移動過程中大盤子不允許出現在小盤子上方。
問:總共需要移動的步數是多少?
因為求的是步數,我們可以通過找前面幾組數據,觀察是否有什么規律
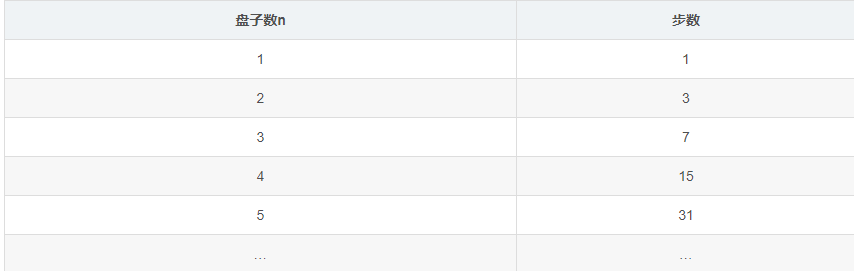
通過表格觀察,可以知道盤子數為n時,步數為20+21+…+2n-1,即2n-1
我們可以通過下面這張圖片來推論:
假設盤子數量為n,通過化繁為簡思想,我們可以把盤子分成兩個部分。上面n-1個盤子,和最下面一個盤子。移動步驟如下:
將最上面的n-1個盤子移動到B柱上
將最下面的盤子移動到C柱上
再將B柱上的n-1個盤子移動到C柱上
問題轉化成如何移動最上面n-1個盤子。按照上面的思路解決n-1個盤子移動的問題。
假設移動n個盤子需要的步數為f(n),則移動n-1個盤子需要f(n-1)步。
故移動步數為f(n)=f(n-1)+1+f(n-1),即f(n)=2*f(n-1)+1
通過等比數列變形又可以得到f(n)=2n-1
代碼5(非遞歸)
#include <stdio.h>
#include <math.h>
int main()
{
int n;
scanf("%d", &n);
int count =0;
count=(int)pow(2,n)-1;
printf("%d", count);
return 0;
}代碼6(遞歸)
#include <stdio.h>
int tower(int n)
{
if (n == 1)
return 1;
else
return 2 * tower(n - 1) + 1;
}
int main()
{
int n;
scanf("%d", &n);
int ret=tower(n);
printf("%d", ret);
return 0;
}有A,B,C三個柱子,A柱子上從上到下,從小到大排列著n個圓盤。現要求將A柱子上的n個圓盤全部移動到C柱子上,依然按照從上到下,從小到大的順序排列。且對移動過程要求如下:
a)一次只能移動一個盤子。
b)移動過程中大盤子不允許出現在小盤子上方。
問:打印移動的方案 (例如, 移動A柱最上面的圓盤到C柱, 則輸出"A -> C")
因為求的是移動方案,所以我們可以將前幾組數據列出來,結合遞歸化簡為繁的思想找共性和非共性

通過觀察得到:除了n=1,n>1時,都是先將A柱上面n-1個盤子拿到B柱(粗字體為其過程),再將A柱最下面盤子拿到C柱。此時A柱變成輔助柱,再將B柱上的盤子放到C柱
故將A柱最下面盤子移到C柱為中間過程
上一步為將初始柱(A柱)上面n-1個盤子借助輔助柱(C柱)移到目標柱(B柱)【其實可以這里看作單獨一個n-1的漢諾塔,將A柱上的盤子移動到B柱】
下一步為將初始柱(B柱)上面n-1個盤子借助輔助柱(A柱)移到目標柱(C柱)【其實可以這里看作單獨一個n-1的漢諾塔,將B柱上的盤子移動到C柱】
而上一步,中間過程,下一布就是遞歸的核心思想
而當n=1時,盤子數只有一個,我們將其直接放到目標柱即可(其為最終的限制條件)
初始柱,輔助柱,目標柱,其實就是把該步驟的移動過程當作一個單獨的漢諾塔問題,需要移動盤子現在所在的位置為初始柱,要將其放到的位置就是目標柱
代碼7(遞歸)
#include <stdio.h>
void hanio(int n, char x, char y, char z)
{
if (n == 1)
printf("%c->%c\n",x,z); //當盤子只剩一個時,直接打印初始柱移動到目標柱的過程
else
{
hanio(n - 1, x, z, y); //將n-1個盤子從起始柱放到目標柱(第一次A->B,第二次B->A,后面往復)
printf("%c->%c\n", x, z); //打印初始柱移動到目標柱的過程
hanio(n - 1, y, x, z); //將n-1個盤子從起始柱放到目標柱(第一次B->C,第二次C->B,后面往復)
}
}
int main()
{
int n;
scanf("%d", &n);
hanio(n,'A','B','C');
return 0;
}到此,關于“C語言經典案例青蛙跳臺階和漢諾塔問題怎么實現”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。