C++約瑟夫環問題實例講解

這篇文章主要講解了“C++約瑟夫環問題實例講解”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“C++約瑟夫環問題實例講解”吧！

在牛客網上做到一道題，是約瑟夫環的變型，所以借此學習一下新知識，并且鞏固一下對題目意思的理解，這一篇僅作約瑟夫環問題的解釋，下一篇再寫題目：

##1.首先，我們先來了解一下什么是約瑟夫環問題：
講一個比較有意思的故事：約瑟夫是猶太軍隊的一個將軍，在反抗羅馬的起義中，他所率領的軍隊被擊潰，只剩下殘余的部隊40余人，他們都是寧死不屈的人，所以不愿投降做叛徒。一群人表決說要死，所以用一種策略來先后kill所有人。
于是約瑟夫建議：每次由其他兩人一起kill一個人，而被kill的人的先后順序是由抽簽決定的，約瑟夫有預謀地抽到了最后一簽，在kill了除了他和剩余那個人之外的最后一人，他勸服了另外一個沒死的人投降了羅馬。

我們這個規則是這么定的：
在一間房間總共有n個人（下標0～n-1），只能有最后一個人活命。

按照如下規則去排除人：

所有人圍成一圈順時針報數，每次報到q的人將被排除掉被排除掉的人將從房間內被移走然后從被kill掉的下一個人重新報數，繼續報q，再清除，直到剩余一人

你要做的是：當你在這一群人之間時，你必須選擇一個位置以使得你變成那剩余的最后一人，也就是活下來。

##2.這就是約瑟夫環問題，接下來我們說個特例初步了解下這種問題的求解思路：

特例：2，當q = 2時候，是一個特例，能快速求解
特例還分兩種

###1.思路：注意這里的前提是n = 2^k(也就是2的冪次個人，其他數另外討論)

如果只有2個人，顯然剩余的為1號

如果有4個人，第一輪除掉2,4，剩下1,3，3死，留下1

如果是8個人，先除去2,4,6,8,之后3,7，剩下1,5，除去5，又剩下1了

定義J(n)為n個人構成的約瑟夫環最后結果，則有j(2^k) = 1

J(n) = 2^k – 2^k-1 = 2^k-1     				n=2^k

J(n) = 2^k-1 – 2^k-2 = 2^k-2    			n=2^k-1

………

J(2^2) = 2^2 – 2^1 = 2^1 					n=2^2

遞推得到如上結果，起始我們仔細分析也就是每次除去一半的元素，然后剩余的一半繼續重復之前的策略，再除去一半。（可想到遞歸）

結合：J(2) = 1 我知道兩個數，從1開始，肯定是2先死，剩下1.

得到：j(2^k) = 1

###2.but當n 不等于 2^k時候，比如9,11這種：

n 不等于 2^k時，就不存在這樣的easy的規律了，重新分析：

假設n = 9，這時候如圖下：

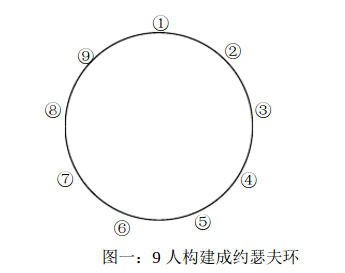
能看出來，我們干掉第一個人也就是2，之后就只剩下8個人了，又回到J(2^k)上了，這時候我們需要的是找到當前的1號元素。
見圖下：

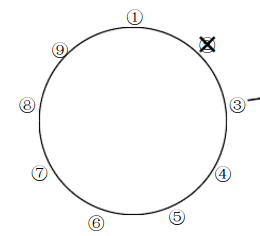
這時候，我們從3號開始，就成了另外一個規模小1的約瑟夫問題（恰好為2^k的特例）。
這時候，我們可以把3號看成新的約瑟夫問題中的1號位置：
J(8) = J(2^3) = 1，也就是說這里的1代表的就是上一個問題中的3號

So：J(9) = 3
答案為3號

####同理可知所有的非2^k的數都是這樣：
假設n = 2^k + t，t可以隨意取，比如1，2，3…….

假設n = 11，這時候n = 2^3 + 3，也就是說t = 3，所以開始剔除元素直到其成為2^k問題的約瑟夫問題。
So，我們在剔除了t（3）個元素之后（分別是2,4,6），此時我們定格在2t+1（7）處，并且將2t+1（7）作為新的一號，而且這時候的約瑟夫環只剩下23，也就是J(23 + 3) = 2*3 + 1 = 7，答案為7

總結一下這個規律：
J(2^k + t) = 2t+1

##3.說完了特例，現在說說q 不等于2的情況下：

當q ≠ 2：

我們假定：

• n — n人構成的約瑟夫環

• q — 每次移除第q個人
  約定：

• Jq(n)表示n人構成的約瑟夫環，每次移除第q個人的解

• n個人的編號從0開始至n-1

我們沿用之前特例的思想：能不能由Jq(n+1)的問題縮小成為J(n)的問題（這里的n是n+1規模的約瑟夫問題消除一個元素之后的答案），Jq(n)是在Jq(n+1)基礎上移除一個人之后的解。也就是說，我們能由Jq(n)得到Jq(n+1)。

規律：Jq(n+1) = ( Jq(n) + q ) / (n+1)
詳細推導過程見這篇博文

大致是如下這樣：

0 1 2 3 4 5 ......  n-1       總共n人
設第q個人也就是下標為q-1的那位，kill：

剩下n-1個人，如下：
q q+1 q+2 ...... n-2  n-1   0  1  2   ......  q-2     (這里是除去q-1這位兄臺的剩余n-1人)

這時，又來重復我們的老套路：將新的被kill的后一個人作為新的0號，于是新的如下：
0  1  2   ......     ..........     ........  n-2

其實就是從q開始，到之前最大數n-1，每個數都減去q,從0開始之后接著n-1這個新的值每次往后加1，直到加到n-1（這個下標）
舉個例子：

J4(9) :
0 1 2 3 4 5 6 7 8    消去3-->    0 1 2 4 5 6 7 8( 0 1 2)
				  對應的新值：	      0 1 2 3 4  5 6 7

其中：q=4，從3之后第一個數4開始：每個數5-q=1,6-q=2,7-q=3，8-q=4，因為是個環，0-q=-4,1-q=-3 ....直到加到n-1=7 

這就相當于一個限定范圍內的數的相對位置，-1代表的是最后一個元素，也就是之前的8
（-2就代表7,-3代表6,-4代表5.....-9代表0，從后面開始數過來第9位）

大致過程如圖下：

那么我們知道是這么得到的新的隊列，那么也很容易知道怎么反推了：
反觀如上的變化情況，都是減去一個q，所以：
變回去的公式如下：old = (new + q) % n
這里的old和new指的是下標，n指的是總共有多少人

知道了怎么推出之前的下標，那么也就可以一步步遞推回去得到開始的隊列或者從小推到大得到最后剩余的結果。

##最后再做一道實際點的例子，求J2(4):
J2(1) = 0
J2(2) = (J2(1) + 2) % 2 = 0
J2(3) = (J2(2) + 2) % 3 = 2
J2(4) = (J2(3) + 2) % 4 = 0
…
這樣一步步求就能得到所有的給出n和q條件的答案了。

#include<iostream>
#include<stdio.h>
using namespace std;

int yuesefu(int n,int m){
        if(n == 1){
                return 0; //這里返回下標,從0開始，只有一個元素就是剩余的元素0
        }
        else{
                return (yuesefu(n-1,m) + m) % n; //我們傳入的n是總共多少個數
        }
}
int main(void){
        int a,b;
        cin>>a>>b;
        cout<<yuesefu(a,b)<<endl;

		//或者，直接循環迭代，求出來的result如上
		int result = 0;
        for(int i = 2;i <= a;i++){
                result = (result+b) %i;
        }
        cout<<"result = "<<result<<endl;
        return 0;
}

##總結：
在遇上包含特殊的出隊規則相關的題目時，應該聯想到是否是約瑟夫環問題，方便求解。
此文章重新整理在約瑟夫環問題詳解里了，修改了之前寫過程中存在的一些錯誤，并添加了一些新的推導過程。

感謝各位的閱讀，以上就是“C++約瑟夫環問題實例講解”的內容了，經過本文的學習后，相信大家對C++約瑟夫環問題實例講解這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！